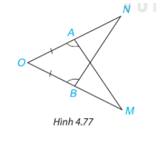
Trong Hình 4.77, có AO = BO,\(\widehat {OAM} = \widehat {OBN}\). Chứng minh rằng AM = BN.
Những câu hỏi liên quan
Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng\(\widehat {MAN} = \widehat {MBN}\).
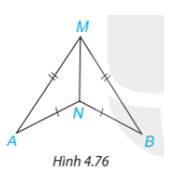
Xét \(\Delta MNA\) và \(\Delta MNB \) có:
AM=BM (gt)
AN=BN (gt)
MN chung
=>\(\Delta MNA = \Delta MNB\) (c.c.c)
=>\(\widehat {MAN} = \widehat {MBN}\) (2 góc tương ứng)
Đúng 0
Bình luận (0)
Cho Hình 65 có AM = BN, \(\widehat A = \widehat B\). Chứng minh: OA = OB, OM = ON.
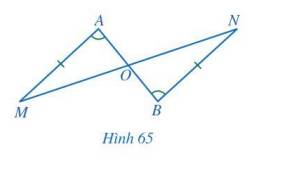
Ta có: \(\widehat A = \widehat B\)
Mà 2 góc này ở vị trí so le trong nên AM // BN
\(\Rightarrow \widehat M = \widehat N\)(2 góc so le trong).
Xét hai tam giác AOM và BON có: \(\widehat A = \widehat B\), AM = BN, \(\widehat M = \widehat N\).
Vậy \(\Delta AOM = \Delta BON\) (g.c.g)
Do đó OA = OB, OM = ON. (2 cạnh tương ứng).
Đúng 0
Bình luận (0)
Cho widehat{xoy} 90 độ . Trên tia ox oy thứ tự lấy a, b ở miền trong widehat{xoy}vẽ các tia Am, Bn sao cho widehat{xAm}50 độ, widehat{yBn} 40 độa, chứng minh Am song song Bnb, gọi E là giao điểm của AO và tia đối của tia Bn. Tính các góc của tam giác EOBc, kẻ OH vuông góc EB tại H. chúng minh OH vuông góc với tia đối của tia AM tại Kd, chứng minh widehat{ACK} widehat{OBE}
Đọc tiếp
Cho \(\widehat{xoy}\)= 90 độ . Trên tia ox oy thứ tự lấy a, b ở miền trong \(\widehat{xoy}\)vẽ các tia Am, Bn sao cho \(\widehat{xAm}\)=50 độ, \(\widehat{yBn}\) =40 độ
a, chứng minh Am song song Bn
b, gọi E là giao điểm của AO và tia đối của tia Bn. Tính các góc của tam giác EOB
c, kẻ OH vuông góc EB tại H. chúng minh OH vuông góc với tia đối của tia AM tại K
d, chứng minh \(\widehat{ACK}\)= \(\widehat{OBE}\)
Trong Hình 4.78, ta có AN = BM,\(\widehat {BAN} = \widehat {ABM}\). Chứng minh rằng\(\widehat {BAM} = \widehat {ABN}\).
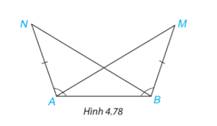
Xét \(\Delta ANB \) và \(\Delta BMA\) có:
AN=BM (gt)
\(\widehat {BAN} = \widehat {ABM}\) (gt)
AB chung
=>\(\Delta ANB = \Delta BMA\)(c.g.c)
=> \(\widehat{ABN} = \widehat{BAM}\) (2 góc tương ứng)
Đúng 0
Bình luận (0)
Cho \(\widehat{xOy}\)= 120. Trên tia Ox ta lấy điểm A. Trên tia Oy ta lấy điểm B (điểm A và B không trùng với điểm O). Vẽ các tia AM và BN ở trong \(\widehat{xOy}\)sao cho \(\widehat{xAm}\)= 70 và \(\widehat{oBn}\)= 130.
CM tia Am // Bn
3 tháng 3 2020 lúc 21:38
1. Cho △ABC có AB là cạnh lớn nhất, BC là cạnh nhỏ nhất. Chứng minh rằng widehat{C}60^o, widehat{A}le60^o.
2. Cho tam giác ABC có M là trung điểm BC.
a) Giả sử AB AC. Chứng minh widehat{MAC} widehat{BAM}
b) Giả sử widehat{MAC} widehat{BAM}. Chứng minh AB AC.
c) Gọi N là trung điểm AC, AM cắt BN tại G. Giả sử AM ⊥ BN. Chứng minh 2AC BC.
3.
a) Cho △ABC cân tại A, D là điểm bất kì trong △ABC sao cho widehat{ADB} widehat{ADC}. Chứng minh BD DC
b) Cho △ABC vuông tại A. Chứng minh rằng AB^...
Đọc tiếp
1. Cho △ABC có AB là cạnh lớn nhất, BC là cạnh nhỏ nhất. Chứng minh rằng \(\widehat{C}>60^o\), \(\widehat{A}\le60^o\).
2. Cho tam giác ABC có M là trung điểm BC.
a) Giả sử AB < AC. Chứng minh \(\widehat{MAC}< \widehat{BAM}\)
b) Giả sử \(\widehat{MAC}< \widehat{BAM}\). Chứng minh AB < AC.
c) Gọi N là trung điểm AC, AM cắt BN tại G. Giả sử AM ⊥ BN. Chứng minh 2AC > BC.
3.
a) Cho △ABC cân tại A, D là điểm bất kì trong △ABC sao cho \(\widehat{ADB}< \widehat{ADC}\). Chứng minh BD > DC
b) Cho △ABC vuông tại A. Chứng minh rằng \(AB^{2017}+AC^{2017}< BC^{2017}\)
Bài 2 :
a, - Kéo dài AM tới điểm D sao cho AM = MD .
- Ta có : \(\widehat{M_1}\) và \(\widehat{M_2}\) đối đỉnh .
=> \(\widehat{M_1}\) = \(\widehat{M_2}\)
- Xét \(\Delta ABM\) và \(\Delta DCM\) có :
\(\left\{{}\begin{matrix}BM=CM\left(GT\right)\\\widehat{M_1}=\widehat{M_2}\left(cmt\right)\\AM=DM\left(GT\right)\end{matrix}\right.\)
=> \(\Delta ABM\) = \(\Delta DCM\) ( c - g - c )
=> \(\widehat{A_1}=\widehat{D_2}\) ( góc tương ứng )
=> \(AB=CD\) ( cạnh tương ứng )
Mà \(AB< AC\left(GT\right)\)
=> \(CD< AC\)
=> \(\widehat{MAC}< \widehat{ADC}\) ( quan hệ cạnh góc đối diện )
Mà \(\widehat{ADC}=\widehat{BAM}\) ( cmt )
=> \(\widehat{BAM}>\widehat{MAC}\) ( đpcm )
3 tháng 3 2020 lúc 22:15
2. Cho tam giác ABC có M là trung điểm BC.a) Giả sử AB AC. Chứng minh widehat{MAC} widehat{BAM}b) Giả sử widehat{MAC} widehat{BAM}. Chứng minh AB AC.c) Gọi N là trung điểm AC, AM cắt BN tại G. Giả sử AM ⊥ BN. Chứng minh 2AC BC.3.a) Cho △ABC cân tại A, D là điểm bất kì trong △ABC sao cho widehat{ADB} widehat{ADC}. Chứng minh BD DCb) Cho △ABC vuông tại A. Chứng minh rằng AB2017+AC2017BC2017
Đọc tiếp
2. Cho tam giác ABC có M là trung điểm BC.
a) Giả sử AB < AC. Chứng minh \(\widehat{MAC}< \widehat{BAM}\)
b) Giả sử \(\widehat{MAC}< \widehat{BAM}\). Chứng minh AB < AC.
c) Gọi N là trung điểm AC, AM cắt BN tại G. Giả sử AM ⊥ BN. Chứng minh 2AC > BC.
3.
a) Cho △ABC cân tại A, D là điểm bất kì trong △ABC sao cho \(\widehat{ADB}< \widehat{ADC}\). Chứng minh BD > DC
b) Cho △ABC vuông tại A. Chứng minh rằng AB2017+AC2017<BC2017
28 tháng 9 2023 lúc 15:47
Cho hình sau, bt widehat{xOy}a. Tính số đo widehat{OAm} để Am//Ox O A x m y a 2 1
Đọc tiếp
Cho hình sau, bt \(\widehat{xOy}=a.\) Tính số đo \(\widehat{OAm}\) để \(Am//Ox\)
\(Am//Ox\Rightarrow\widehat{xOy}=\widehat{mAy}=a\)
\(\Rightarrow\widehat{OAm}=180^o-\widehat{mAy}=180^o-a\)
Đúng 1
Bình luận (0)
`#3107`
Ta có:
`\text {AM // Ox}`
`=>` \(\widehat{\text{xOA}}=\widehat{\text{A}_1}\) (2 góc đồng vị)
Mà \(\widehat{\text{A}_1}\) và \(\widehat{\text{OAm}}\) là 2 góc kề bù
`=>`\(\widehat{\text{A}_1}+\widehat{\text{OAm}}=180^0\)
`=>`\(\widehat{\text{xOA}}+\widehat{\text{OAm}}=180^0\)
`=>`\(a+\widehat{\text{ }\text{OAm}}=180^0\)
`=>`\(\widehat{\text{OAm}}=180^0-a\)
Vậy, để `\text {AM // Ox}` thì cần thỏa mãn \(\widehat{\text{OAm}}=180^0-a.\)
Đúng 0
Bình luận (0)