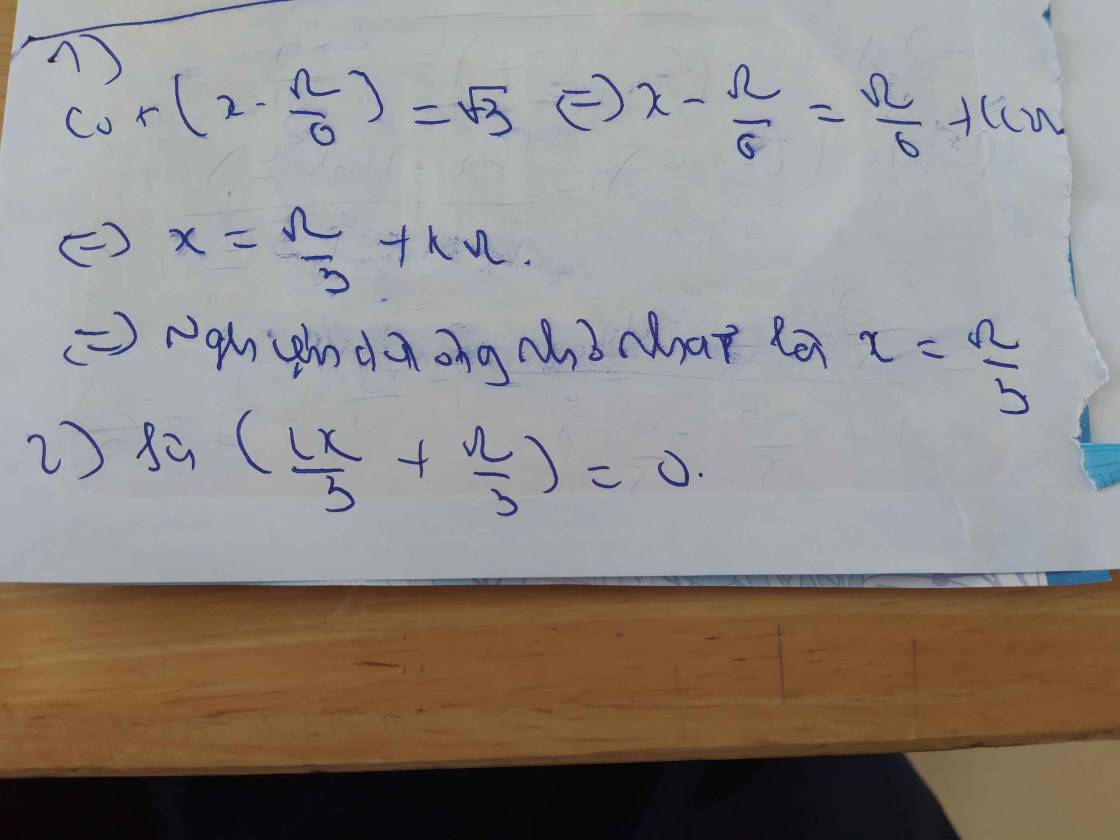\(\sqrt{2-f\left(x\right)}=f\left(x\right)\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)\ge0\\f^2\left(x\right)+f\left(x\right)-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-2< 0\left(loại\right)\end{matrix}\right.\) 

\(\Rightarrow f\left(1\right)=f\left(2\right)=f\left(3\right)=1\)

\(\sqrt{2g\left(x\right)-1}+\sqrt[3]{3g\left(x\right)-2}=2.g\left(x\right)\)

\(VT=1.\sqrt{2g\left(x\right)-1}+1.1\sqrt[3]{3g\left(x\right)-2}\)

\(VT\le\dfrac{1}{2}\left(1+2g\left(x\right)-1\right)+\dfrac{1}{3}\left(1+1+3g\left(x\right)-2\right)\)

\(\Leftrightarrow VT\le2g\left(x\right)\)

Dấu "=" xảy ra khi và chỉ khi \(g\left(x\right)=1\)

\(\Rightarrow g\left(0\right)=g\left(3\right)=g\left(4\right)=g\left(5\right)=1\)

Để các căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)-1\ge0\\g\left(x\right)-1\ge0\end{matrix}\right.\)

Ta có:

\(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)-f\left(x\right)-g\left(x\right)+1=0\)

\(\Leftrightarrow\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+\left[f\left(x\right)-1\right]\left[g\left(x\right)-1\right]=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\g\left(x\right)=1\end{matrix}\right.\) \(\Leftrightarrow x=3\)

Vậy tập nghiệm của pt đã cho có đúng 1 phần tử

\(\sqrt{4x-8}-2\sqrt{\dfrac{x-2}{4}}=3\left(x\ge2\right)\\ \Leftrightarrow2\sqrt{x-2}-\sqrt{x-2}=3\\ \Leftrightarrow\sqrt{x-2}=3\Leftrightarrow x-2=9\\ \Leftrightarrow x=11\left(tm\right)\)

ĐKXĐ: \(x\ge2\)

\(pt\Leftrightarrow2\sqrt{x-2}-\sqrt{x-2}=3\)

\(\Leftrightarrow\sqrt{x-2}=3\Leftrightarrow x-2=9\Leftrightarrow x=11\left(tm\right)\)

ĐKXĐ: \(3\ge x\ge5\)(vô lý)

Vậy pt vô nghiệm

Lời giải:

PT $\Leftrightarrow \sqrt{x+y+3}=\sqrt{x}+\sqrt{y}-1$

$\Rightarrow x+y+3=(\sqrt{x}+\sqrt{y}-1)^2$

$\Leftrightarrow x+y+3=x+y+1-2(\sqrt{x}+\sqrt{y}-\sqrt{xy})$

$\Leftrightarrow 1+\sqrt{x}+\sqrt{y}-\sqrt{xy}=0(*)$

$\Rightarrow (\sqrt{x}+\sqrt{y})^2=(\sqrt{xy}-1)^2$

$\Rightarrow 4\sqrt{xy}=xy+1-x-y\in\mathbb{Z}$

Ta có nhận xét sau: Với số không âm $a$ bất kỳ thì khi $\sqrt{a}$ là số hữu tỉ thì $\sqrt{a}$ cũng là số chính phương.

Do đó: $\sqrt{xy}$ là scp

Kết hợp $(*)$ suy ra $\sqrt{x}+\sqrt{y}\in\mathbb{Z}$

$\sqrt{x}(\sqrt{x}+\sqrt{y})=x+\sqrt{xy}\in\mathbb{Z}$

$\Rightarrow \sqrt{x}=\frac{x+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\in\mathbb{Q}$

$\Rightarrow \sqrt{x}$ là scp. Kéo theo $\sqrt{y}$ là scp.

Từ $(*)$ ta cũng có $(\sqrt{x}-1)(1-\sqrt{y})=-2$

Đến đây thì với $\sqrt{x}, \sqrt{y}\in\mathbb{Z}$ ta có pt tích khá đơn giản.

Giải:

Tập xác định của phương trình

Tập xác định của phương trình

Biến đổi vế trái của phương trình

Biến đổi vế phải của phương trình

Phương trình thu được sau khi biến đổi

Biến đổi vế trái của phương trình

Phương trình thu được sau khi biến đổi

Đơn giản biểu thức

Giải phương trình

\(\Leftrightarrow\sqrt{\left(\sqrt{x+7}-1\right)^2}+\sqrt{x+1-\sqrt{x+7}}=2\)

ĐKXĐ: \(\left\{{}\begin{matrix}x+7\ge0\\x+1-\sqrt{x+7}\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-7\\x\ge-1\\\left(x+1\right)^2\ge x+7\end{matrix}\right.\) \(\Leftrightarrow x\ge2\)

Khi đó pt tương đương:

\(\left|\sqrt{x+7}-1\right|+\sqrt{x+1-\sqrt{x+7}}=2\)

\(\Leftrightarrow\sqrt{x+7}+\sqrt{x+1-\sqrt{x+7}}=3\)

Do \(x\ge2\Rightarrow\left\{{}\begin{matrix}\sqrt{x+7}\ge\sqrt{2+7}=3\\\sqrt{x+1-\sqrt{x+7}}\ge0\end{matrix}\right.\)

\(\Rightarrow\sqrt{x+7}+\sqrt{x+1-\sqrt{x+7}}\ge3\)

Dấu "=" xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}\sqrt{x+7}=3\\\sqrt{x+1-\sqrt{x+7}}=0\end{matrix}\right.\) \(\Leftrightarrow x=2\)

Pt có đúng 1 nghiệm

ĐK: \(x\ge2\)

\(pt\Leftrightarrow\sqrt{x-2}=3\sqrt{x^2-4}\)

\(\Leftrightarrow x-2=9x^2-36\)

\(\Leftrightarrow9x^2-x-34=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{17}{9}\left(l\right)\end{matrix}\right.\)

\(\Rightarrow x^2=4\)

\(\left(1+x\sqrt{x^2+1}\right)\left(\sqrt{x^2+1}-x\right)=1\)

\(\Rightarrow\dfrac{1+x\sqrt{x^2+1}}{\sqrt{x^2+1}+x}=1\)

\(\Rightarrow1+x\sqrt{x^2+1}=\sqrt{x^2+1}+x\)

\(\Rightarrow1+x\sqrt{x^2+1}-\sqrt{x^2+1}-x=0\)

\(\Rightarrow-\left(x-1\right)+\left(x-1\right)\sqrt{x^2+1}=0\)

\(\Rightarrow\left(x-1\right)\left(\sqrt{x^2+1}-1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x-1=0\\\sqrt{x^2+1}-1=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=1\\\sqrt{x^2+1}=1\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=1\\x^2+1=1\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\)

\(a,2y^2-x+2xy=y+4\\ \Leftrightarrow2y\left(x+y\right)-\left(x+y\right)=4\\ \Leftrightarrow\left(2y-1\right)\left(x+y\right)=4=4\cdot1=\left(-4\right)\left(-1\right)=\left(-2\right)\left(-2\right)=2\cdot2\)

Vì \(x,y\in Z\Leftrightarrow2y-1\) lẻ 

\(\left\{{}\begin{matrix}2y-1=1\\x+y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2y-1=-1\\x+y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)

Vậy PT có nghiệm \(\left(x;y\right)=\left\{\left(3;1\right);\left(4;0\right)\right\}\)

\(\sqrt{x+y+3}+1=\sqrt{x}+\sqrt{y}\)

Bình phương 2 vế, ta có:

\(x+y+3+1=x+y\)

\(x+y+3+1-x-y=0\)

\(4=0\) (vô lý)

Vậy phương trình vô nghiệm

-Chúc bạn học tốt-

(x,y) hoán vị của (4,9) . có vẻ hoạt động

S=(1;2]

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+2=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=7\end{matrix}\right.\)

\(ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{x-2}\left(\sqrt{x+2}-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x-2}=0\\\sqrt{x+2}=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+2=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=7\left(tm\right)\end{matrix}\right.\)

ĐK:x≥2PT⇔√x−2(√x+2−3)=0⇔[√x−2=0√x+2=3⇔[x−2=0x+2=9⇔[x=2(tm)x=7(tm)