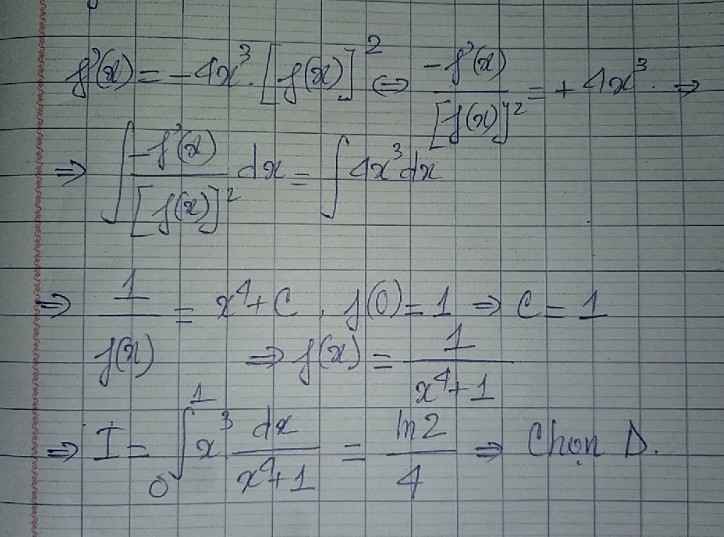\(h\left(x\right)=f\left(x^2+1\right)-m\Rightarrow h'\left(x\right)=2x.f'\left(x^2+1\right)\)

\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(x^2+1\right)=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x^2+1=2\\x^2+1=5\end{matrix}\right.\) \(\Rightarrow x=\left\{-2;-1;0;1;2\right\}\)

Hàm có nhiều cực trị nhất khi \(h\left(x\right)=m\) có nhiều nghiệm nhất

\(f\left(x\right)=\int f\left(x\right)dx=\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x+C\)

\(f\left(1\right)=0\Rightarrow C=-\dfrac{199}{12}\Rightarrow f\left(x\right)=-\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x-\dfrac{199}{12}\)

\(x=\pm2\Rightarrow x^2+1=5\Rightarrow f\left(5\right)\approx-18,6\)

\(x=\pm1\Rightarrow x^2+1=2\Rightarrow f\left(2\right)\approx6,1\)

\(x=0\Rightarrow x^2+1=1\Rightarrow f\left(1\right)=0\)

Từ đó ta phác thảo BBT của \(f\left(x^2+1\right)\) có dạng:

Từ đó ta dễ dàng thấy được pt \(f\left(x^2+1\right)=m\) có nhiều nghiệm nhất khi \(0< m< 6,1\)

\(\Rightarrow\) Có 6 giá trị nguyên của m

Xét \(I=\int\limits^1_0x^2f\left(x\right)dx\)

Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=x^2dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=\dfrac{1}{3}x^3\end{matrix}\right.\)

\(\Rightarrow I=\dfrac{1}{3}x^3.f\left(x\right)|^1_0-\dfrac{1}{3}\int\limits^1_0x^3.f'\left(x\right)dx=-\dfrac{1}{3}\int\limits^1_0x^3f'\left(x\right)dx\)

\(\Rightarrow\int\limits^1_0x^3f'\left(x\right)dx=-1\)

Lại có: \(\int\limits^1_0x^6.dx=\dfrac{1}{7}\)

\(\Rightarrow\int\limits^1_0\left[f'\left(x\right)\right]^2dx+14\int\limits^1_0x^3.f'\left(x\right)dx+49.\int\limits^1_0x^6dx=0\)

\(\Rightarrow\int\limits^1_0\left[f'\left(x\right)+7x^3\right]^2dx=0\)

\(\Rightarrow f'\left(x\right)+7x^3=0\)

\(\Rightarrow f'\left(x\right)=-7x^3\)

\(\Rightarrow f\left(x\right)=\int-7x^3dx=-\dfrac{7}{4}x^4+C\)

\(f\left(1\right)=0\Rightarrow C=\dfrac{7}{4}\)

\(\Rightarrow I=\int\limits^1_0\left(-\dfrac{7}{4}x^4+\dfrac{7}{4}\right)dx=...\)

\(f'\left(x\right)=-4x^3\left(f\left(x\right)\right)^2\Leftrightarrow-\dfrac{f'\left(x\right)}{\left(f\left(x\right)\right)^2}=4x^3\)

Lấy nguyên hàm hai vế

\(\int-\dfrac{f'\left(x\right)}{\left(f\left(x\right)\right)^2}dx=\int4x^3dx\)

\(\Leftrightarrow\dfrac{1}{f\left(x\right)}=x^4+c\)

Thay x=0 vào tìm được c=1 \(\Rightarrow f\left(x\right)=\dfrac{1}{x^4+1}\)

\(I=\int\limits^1_0\dfrac{x^3}{x^4+1}dx=\dfrac{1}{4}\int\limits^1_0\dfrac{\left(x^4+1\right)'}{x^4+1}dx=\dfrac{ln2}{4}\)

Chọn D

\(2x.f'\left(x\right)-f\left(x\right)=x^2\sqrt{x}.cosx\)

\(\Leftrightarrow\dfrac{1}{\sqrt{x}}.f'\left(x\right)-\dfrac{1}{2x\sqrt{x}}f\left(x\right)=x.cosx\)

\(\Leftrightarrow\left[\dfrac{f\left(x\right)}{\sqrt{x}}\right]'=x.cosx\)

Lấy nguyên hàm 2 vế:

\(\int\left[\dfrac{f\left(x\right)}{\sqrt{x}}\right]'dx=\int x.cosxdx\)

\(\Rightarrow\dfrac{f\left(x\right)}{\sqrt{x}}=x.sinx+cosx+C\)

\(\Rightarrow f\left(x\right)=x\sqrt{x}.sinx+\sqrt{x}.cosx+C.\sqrt{x}\)

Thay \(x=4\pi\)

\(\Rightarrow0=4\pi.\sqrt{4\pi}.sin\left(4\pi\right)+\sqrt{4\pi}.cos\left(4\pi\right)+C.\sqrt{4\pi}\)

\(\Rightarrow C=-1\)

\(\Rightarrow f\left(x\right)=x\sqrt{x}.sinx+\sqrt{x}.cosx-\sqrt{x}\)

1. Áp dụng quy tắc L'Hopital

\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-1}{f\left(0\right)-f\left(x\right)}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{1}{2\sqrt{x+1}}}{-f'\left(0\right)}=-\dfrac{1}{6}\)

2.

\(g'\left(x\right)=2x.f'\left(\sqrt{x^2+4}\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(\sqrt{x^2+4}\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\sqrt{x^2+4}=1\\\sqrt{x^2+4}=-2\end{matrix}\right.\) 

2 pt cuối đều vô nghiệm nên \(g'\left(x\right)=0\) có đúng 1 nghiệm

\(f\left(x\right)-\left(x+1\right)f'\left(x\right)=2x.f^2\left(x\right)\)

\(\Rightarrow\dfrac{f\left(x\right)-\left(x+1\right)f'\left(x\right)}{f^2\left(x\right)}=2x\)

\(\Rightarrow\left[\dfrac{x+1}{f\left(x\right)}\right]'=2x\)

Lấy nguyên hàm 2 vế:

\(\dfrac{x+1}{f\left(x\right)}=\int2xdx=x^2+C\)

Thay \(x=1\Rightarrow\dfrac{2}{f\left(1\right)}=1+C\Rightarrow C=0\)

\(\Rightarrow f\left(x\right)=\dfrac{x+1}{x^2}\Rightarrow\int\limits^2_1\left(\dfrac{1}{x}+\dfrac{1}{x^2}\right)dx=\left(lnx-\dfrac{1}{x}\right)|^2_1=ln2+\dfrac{1}{2}\)

C

C

Cho hàm số y=f(x)y=f(x) có đạo hàm và liên tục trên [0;π2][0;π2]thoả mãn f(x)=f′(x)−2cosxf(x)=f′(x)−2cosx. Biết f(π2)=1f(π2)=1, tính giá trị f(π3)f(π3)

A. √3+1/2         B. √3−1/2          C. 1−√3/2             D. 0

B

\(f'\left(x\right)-f\left(x\right)=2cosx\)

\(\Leftrightarrow e^{-x}.f'\left(x\right)-e^{-x}.f\left(x\right)=2e^{-x}cosx\)

\(\Rightarrow\left[e^{-x}.f\left(x\right)\right]'=2e^{-x}.cosx\)

Lấy nguyên hàm 2 vế:

\(\Rightarrow e^{-x}.f\left(x\right)=\int2e^{-x}cosxdx=e^{-x}\left(sinx-cosx\right)+C\)

Thay \(x=\dfrac{\pi}{2}\Rightarrow e^{-\dfrac{\pi}{2}}.1=e^{-\dfrac{\pi}{2}}+C\Rightarrow C=0\)

\(\Rightarrow f\left(x\right)=sinx-cosx\)

\(\Rightarrow f\left(\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}-1}{2}\)

Chọn B

B

Đang học Lý mà thấy bài nguyên hàm hay hay nên nhảy vô luôn :b

\(I_1=\int\limits^1_0xf\left(x\right)dx\)

\(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=xdx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=\dfrac{1}{2}x^2\end{matrix}\right.\)

\(\Rightarrow\int xf\left(x\right)dx=\dfrac{1}{2}x^2f\left(x\right)-\dfrac{1}{2}\int x^2f'\left(x\right)dx\)

\(\Rightarrow\int\limits^1_0xf\left(x\right)dx=\dfrac{1}{2}x^2|^1_0-\dfrac{1}{2}\int\limits^1_0x^2f'\left(x\right)dx=\dfrac{1}{5}\)

\(\Leftrightarrow\dfrac{1}{2}\int\limits^1_0\left[f'\left(x\right)\right]^2dx=\dfrac{3}{10}\Rightarrow\int\limits^1_0x^2f'\left(x\right)dx=\dfrac{3}{5}\)

Đoạn này hơi rối xíu, ông để ý kỹ nhé, nhận thấy ta có 2 dữ kiện đã biết, là: \(\int\limits^1_0\left[f'\left(x\right)\right]^2dx=\dfrac{9}{5}and\int\limits^1_0x^2f'\left(x\right)dx=\dfrac{3}{5}\) có gì đó liên quan đến hằng đẳng thức, nên ta sẽ sử dụng luôn

\(\int\limits^1_0\left[f'\left(x\right)+tx^2\right]^2dx=0\)

\(\Leftrightarrow\int\limits^1_0\left[f'\left(x\right)\right]^2dx+2t\int\limits^1_0x^2f'\left(x\right)dx+t^2\int\limits^1_0x^4dx=0\)

\(\Leftrightarrow\dfrac{9}{5}+\dfrac{6}{5}t+\dfrac{1}{5}t^2=0\)  \(\left(\int\limits^1_0x^4dx=\dfrac{1}{5}x^5|^1_0=\dfrac{1}{5}\right)\)\(\)\(\Leftrightarrow t=-3\Rightarrow\int\limits^1_0\left[f'\left(x\right)-3x^2\right]^2dx=0\)

\(\Leftrightarrow f'\left(x\right)=3x^2\Leftrightarrow f\left(x\right)=x^3+C\)

\(\Rightarrow\int\limits^1_0f\left(x\right)dx=\int\limits^1_0x^3dx=\dfrac{1}{4}x^4|^1_0=\dfrac{1}{4}\)

P/s: Có gì ko hiểu hỏi mình nhé !