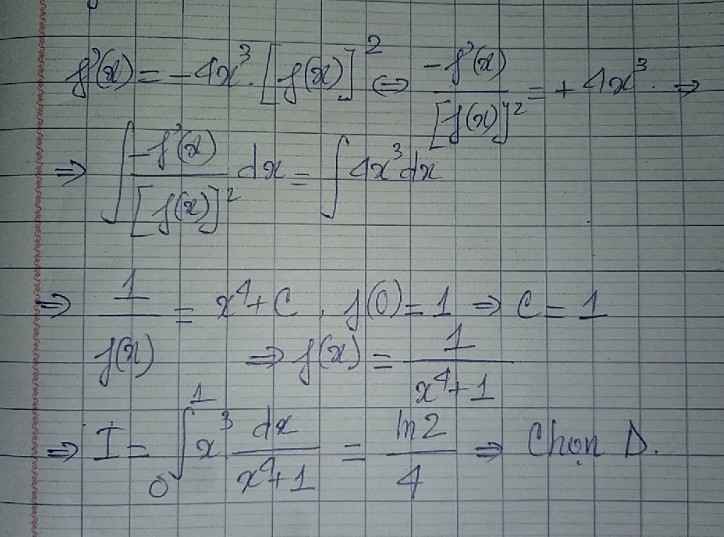Cho hàm số \(f\left(x\right)\) có đạo hàm \(f'\left(x\right)\) liên tục trên \(R\) và thỏa mãn các điều kiện \(f\left(x\right)>0,\forall x\in R\), \(f\left(0\right)=1\) và \(f'\left(x\right)=-4x^3.\left(f\left(x\right)\right)^2,\forall x\in R\). Tính \(I=\int_0^1x^3f\left(x\right)dx\)
A.\(I=\dfrac{1}{6}\) B. \(I=ln2\) C. \(I=\dfrac{1}{4}\) D. \(I=\dfrac{ln2}{4}\)
Mình cần bài giải ạ, mình cảm ơn nhiều♥

\(f'\left(x\right)=-4x^3\left(f\left(x\right)\right)^2\Leftrightarrow-\dfrac{f'\left(x\right)}{\left(f\left(x\right)\right)^2}=4x^3\)
Lấy nguyên hàm hai vế
\(\int-\dfrac{f'\left(x\right)}{\left(f\left(x\right)\right)^2}dx=\int4x^3dx\)
\(\Leftrightarrow\dfrac{1}{f\left(x\right)}=x^4+c\)
Thay x=0 vào tìm được c=1 \(\Rightarrow f\left(x\right)=\dfrac{1}{x^4+1}\)
\(I=\int\limits^1_0\dfrac{x^3}{x^4+1}dx=\dfrac{1}{4}\int\limits^1_0\dfrac{\left(x^4+1\right)'}{x^4+1}dx=\dfrac{ln2}{4}\)
Chọn D