\(a,\left(x-6\right)\left(2x-5\right)\left(3x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x-6=0\Leftrightarrow x=6\\2x-5=0\Leftrightarrow x=\dfrac{5}{2}\\3x+9=0\Leftrightarrow x=-3\end{matrix}\right.\)

\(b,2x\left(x-3\right)+5\left(x-3\right)=0\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-3=0\Leftrightarrow x=3\\2x+5=0\Leftrightarrow x=-\dfrac{5}{2}\end{matrix}\right.\)

\(c,x^2-4-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)

\(x=-7\left(2m-5\right)x-2m^2+8\Leftrightarrow x+7\left(2m-5\right)=8-2m^2\Leftrightarrow x\left(14m-34\right)=8-2m^2\)

\(ycđb\Leftrightarrow14m-34\ne0\Leftrightarrow m\ne\dfrac{34}{14}\)\(\Rightarrow x=\dfrac{8-2m^2}{14m-34}\)

\(3.17\Leftrightarrow4x^2-4x+1-2x-1=0\Leftrightarrow4x^2-6x=0\Leftrightarrow x\left(4x-6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)

3.15:

a, \(\Leftrightarrow\left\{{}\begin{matrix}x-6=0\\2x-5=0\\3x+9=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\x=\dfrac{5}{2}\\x=-\dfrac{9}{3}=-3\end{matrix}\right.\)

b, \(\Leftrightarrow\left(x-3\right)\left(2x+5\right)=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\2x+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)

c, \(\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\3x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)

3.16

\(\Leftrightarrow\left(2m-5\right).-7-2m^2+8=0\)

\(\Leftrightarrow-14m+35-2m^2+8=0\)

\(\Leftrightarrow-14m-2m^2+43=0\)

\(\Leftrightarrow-2\left(7m+m^2\right)=-43\)

\(\Leftrightarrow m\left(7-m\right)=\dfrac{43}{2}\)

\(\Leftrightarrow\dfrac{m\left(7-m\right)}{1}-\dfrac{43}{2}=0\)

\(\Leftrightarrow\dfrac{14m-2m^2}{2}-\dfrac{43}{2}=0\)

pt vô nghiệm

Đặt \(y=x^2-2x+3=\left(x-1\right)^2+2\ge2\), ta có:

\(x^2-2x+3=\frac{6}{x^2-2x+4}\Leftrightarrow y=\frac{6}{y+1}\Leftrightarrow y\left(y+1\right)=6\Leftrightarrow y^2+y-6=0\)

\(\Leftrightarrow\left(y+3\right)\left(y-2\right)=0\Leftrightarrow\orbr{\begin{cases}y=2\\y=-3\end{cases}\Rightarrow y=2\Leftrightarrow\left(x-1\right)^2=0\Leftrightarrow x=1}\)

Vậy \(S=\left\{1\right\}\)

Bài `1:`

`h)(3/4x-1)(5/3x+2)=0`

`=>[(3/4x-1=0),(5/3x+2=0):}=>[(x=4/3),(x=-6/5):}`

______________

Bài `2:`

`b)3x-15=2x(x-5)`

`<=>3(x-5)-2x(x-5)=0`

`<=>(x-5)(3-2x)=0<=>[(x=5),(x=3/2):}`

`d)x(x+6)-7x-42=0`

`<=>x(x+6)-7(x+6)=0`

`<=>(x+6)(x-7)=0<=>[(x=-6),(x=7):}`

`f)x^3-2x^2-(x-2)=0`

`<=>x^2(x-2)-(x-2)=0`

`<=>(x-2)(x^2-1)=0<=>[(x=2),(x^2=1<=>x=+-2):}`

`h)(3x-1)(6x+1)=(x+7)(3x-1)`

`<=>18x^2+3x-6x-1=3x^2-x+21x-7`

`<=>15x^2-23x+6=0<=>15x^2-5x-18x+6=0`

`<=>(3x-1)(5x-1)=0<=>[(x=1/3),(x=1/5):}`

`j)(2x-5)^2-(x+2)^2=0`

`<=>(2x-5-x-2)(2x-5+x+2)=0`

`<=>(x-7)(3x-3)=0<=>[(x=7),(x=1):}`

`w)x^2-x-12=0`

`<=>x^2-4x+3x-12=0`

`<=>(x-4)(x+3)=0<=>[(x=4),(x=-3):}`

`m)(1-x)(5x+3)=(3x-7)(x-1)`

`<=>(1-x)(5x+3)+(1-x)(3x-7)=0`

`<=>(1-x)(5x+3+3x-7)=0`

`<=>(1-x)(8x-4)=0<=>[(x=1),(x=1/2):}`

`p)(2x-1)^2-4=0`

`<=>(2x-1-2)(2x-1+2)=0`

`<=>(2x-3)(2x+1)=0<=>[(x=3/2),(x=-1/2):}`

`r)(2x-1)^2=49`

`<=>(2x-1-7)(2x-1+7)=0`

`<=>(2x-8)(2x+6)=0<=>[(x=4),(x=-3):}`

`t)(5x-3)^2-(4x-7)^2=0`

`<=>(5x-3-4x+7)(5x-3+4x-7)=0`

`<=>(x+4)(9x-10)=0<=>[(x=-4),(x=10/9):}`

`u)x^2-10x+16=0`

`<=>x^2-8x-2x+16=0`

`<=>(x-2)(x-8)=0<=>[(x=2),(x=8):}`

ĐKXĐ: \(x\ne-2;-3;-1\)

PT \(\Leftrightarrow\dfrac{x}{\left(x+2\right)\left(x+3\right)}-\dfrac{2}{\left(x+1\right)\left(x+2\right)}=0\)

\(\Leftrightarrow\dfrac{x^2+x-2x-6}{\left(x+1\right)\left(x+2\right)\left(x+3\right)}=0\)

\(\Leftrightarrow x^2-x-6=0\)

\(\Leftrightarrow x^2+2x-3x-6=0\) 

\(\Leftrightarrow x\left(x+2\right)-3\left(x+2\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(x+2\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\left(loại\right)\end{matrix}\right.\)

  Vậy \(x=3\)

ĐKXĐ của phương trình là: \(x\ne-2;x\ne-3;x\ne-1\)

Ta có: \(\dfrac{x}{x^2+5x+6}=\dfrac{x}{x^2+3x+2}\)

<=> \(\dfrac{x}{\left(x+2\right)\left(x+3\right)}=\dfrac{x}{\left(x+2\right)\left(x+1\right)}\)

<=> \(\dfrac{x\left(x+1\right)}{\left(x+2\right)\left(x+3\right)\left(x+1\right)}-\dfrac{x\left(x+3\right)}{\left(x+2\right)\left(x+1\right)\left(x+3\right)}=0\)

<=> \(\dfrac{x^2+x-x^2-3x}{\left(x+2\right)\left(x+3\right)\left(x+1\right)}=0\)

<=> \(-2x=0\Leftrightarrow x=0\)

Ta thấy x=0 thỏa mãn ĐKXĐ

Vậy tập nghiệm của pt là S={0}

\(a,\\ \Leftrightarrow3x-x=10-6\\ \Leftrightarrow2x=4\\ \Leftrightarrow x=2\\ b,\\ \Leftrightarrow\left(x-2\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)

\(a,\Leftrightarrow3x-x=10-6\\ \Leftrightarrow2x=4\\ \Leftrightarrow x=\dfrac{4}{2}=2\)

Vậy phương trình có tập nghiệm S = \(\left\{2\right\}\)

\(b,\Leftrightarrow\left(x+1\right)\left(x-2\right)=0\\ \Leftrightarrow x+1=0\)           hoặc            \(\Leftrightarrow x-2=0\)       

\(\Leftrightarrow x=-1\)                                                     \(\Leftrightarrow x=2\)

Vậy phương trình có tập nghiệm S = \(\left\{-1;2\right\}\)

a)3x + 6 = x +10
 ⟺3x-x=10-6
 ⟺2x=4 ⟺x=2
Vậy tập nghiệm của phương trình là S={2}
b) x(x + 1) - 2 (x + 1) = 0
 ⟺(x+1)(x-2)=0
 ⟺x+1=0        ⟺x=-1
     x-2=0         ⟺x=2
Vậy tập nghiệm của phương trình là S={2;-1}

Ta có:

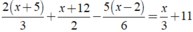
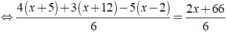
⇔ 4x + 20 + 3x + 36 - 5x + 10 = 2x + 66

⇔ 0x = 0

⇒ Phương trình đã cho vô số nghiệm.

Vậy phương trình đã cho vô số nghiệm.

1/ \(x=3\) 

2/ \(x=3\) hoặc \(x=1\)

 a, \(x^2-\left(2m+1\right)x+m^2+5m=0\)

Với m=2 

\(x^2-\left[2.\left(-2\right)+1\right]x+\left(-2\right)^2+5.\left(-2\right)=0\)

\(x^2+3x-6=0\)

\(\Delta=3^2-4.1.\left(-6\right)\)

     \(=9+24\)

\(=33>0\Rightarrow\sqrt{\Delta}=\sqrt{33}\)

\(\Rightarrow\)Phương trình có 2 nghiệm phân biệt:

\(x_1=\dfrac{-3+\sqrt{33}}{2}\)

\(x_2=\dfrac{-3-\sqrt{33}}{2}\)

Vậy khi m=-2 thì phương trình có nghiệm là \(x_1=\dfrac{-3+\sqrt{33}}{2};x_2=\dfrac{-3-\sqrt{33}}{2}\)

b,Ta có \(\Delta=\left[-\left(2m+1\right)\right]^2-4\left(m^2+5m\right)\)

                 \(=4m^2+4m+1-4m^2-20m\)

                 \(=1-16m\)

Phương trình có 2 nghiệm\(\Leftrightarrow\Delta\ge0\)

                                          \(\Leftrightarrow1-16m\ge0\)

                                          \(\Leftrightarrow m\le\dfrac{1}{16}\)

Khi đó hệ thức viet ta có tích các nghiệm là\(m^2+5m\)

Mà tích các nghiệm bằng 6, do đó \(m^2+5m=6\)

                                                   \(\Leftrightarrow m^2+5m-6=0\)

Ta thấy \(a+b+c=1+5+\left(-6\right)=0\) nên \(m_1=1;m_2=-6\)

Đối chiếu với điều kiện \(m\le\dfrac{1}{16}\) thì \(m=-6\) là giá trị cần tìm

-Chúc bạn học tốt-

\(7x+6\sqrt{x+5}=x^2+30\left(đk:x\ge-5\right)\)

\(\Leftrightarrow6\sqrt{x+5}=x^2-7x+30\)

Ta thấy 2 vế đều dương nên bình phương lên ta được:

\(36x+180=x^4+49x^2+900-14x^3+60x^2-420x\)

\(\Leftrightarrow x^4-14x^3+109x^2-456x+720=0\)

\(\Leftrightarrow x^3\left(x-4\right)-10x^2\left(x-4\right)+69x\left(x-4\right)-180\left(x-4\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x^3-10x^2+69x-180\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left[x^2\left(x-4\right)-6x\left(x-4\right)+45\left(x-4\right)\right]=0\)

\(\Leftrightarrow\left(x-4\right)^2\left(x^2-6x+45\right)=0\)

\(\Leftrightarrow x=4\left(tm\right)\) (do \(x^2-6x+45=\left(x^2-6x+9\right)+36=\left(x-3\right)^2+36\ge36>0\))

a) \(\sqrt {2 - x}  + 2x = 3\)\( \Leftrightarrow \sqrt {2 - x}  = 3 - 2x\)  (1)

Ta có: \(3 - 2x \ge 0 \Leftrightarrow x \le \frac{3}{2}\)

Bình phương hai vế của (1) ta được:

\(\begin{array}{l}2 - x = {\left( {3 - 2x} \right)^2}\\ \Rightarrow 2 - x = 9 - 12x + 4{x^2}\\ \Leftrightarrow 4{x^2} - 11x + 7 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {TM} \right)\\x = \frac{7}{4}\left( {KTM} \right)\end{array} \right.\end{array}\)

Vậy tập nghiệm của phương trình là \(S = \left\{ 1 \right\}\)

b) \(\sqrt { - {x^2} + 7x - 6}  + x = 4\)\( \Leftrightarrow \sqrt { - {x^2} + 7x - 6}  = 4 - x\)  (2)

Ta có: \(4 - x \ge 0 \Leftrightarrow x \le 4\)

Bình phương hai vế của (2) ta được:

\(\begin{array}{l} - {x^2} + 7x - 6 = {\left( {4 - x} \right)^2}\\ \Leftrightarrow  - {x^2} + 7x - 6 = 16 - 8x + {x^2}\\ \Leftrightarrow 2{x^2} - 15x + 22 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\left( {TM} \right)\\x = \frac{{11}}{2}\left( {KTM} \right)\end{array} \right.\end{array}\)

Vậy tập nghiệm của phương trình là \(S = \left\{ 2 \right\}\)