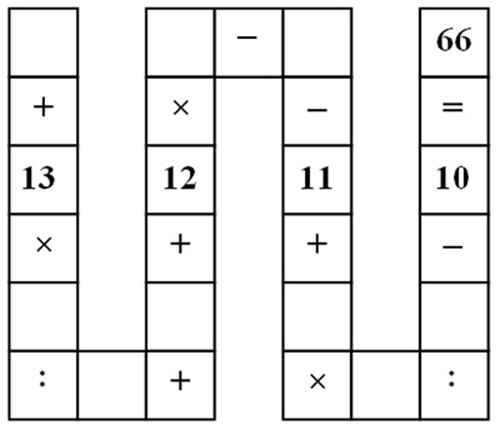
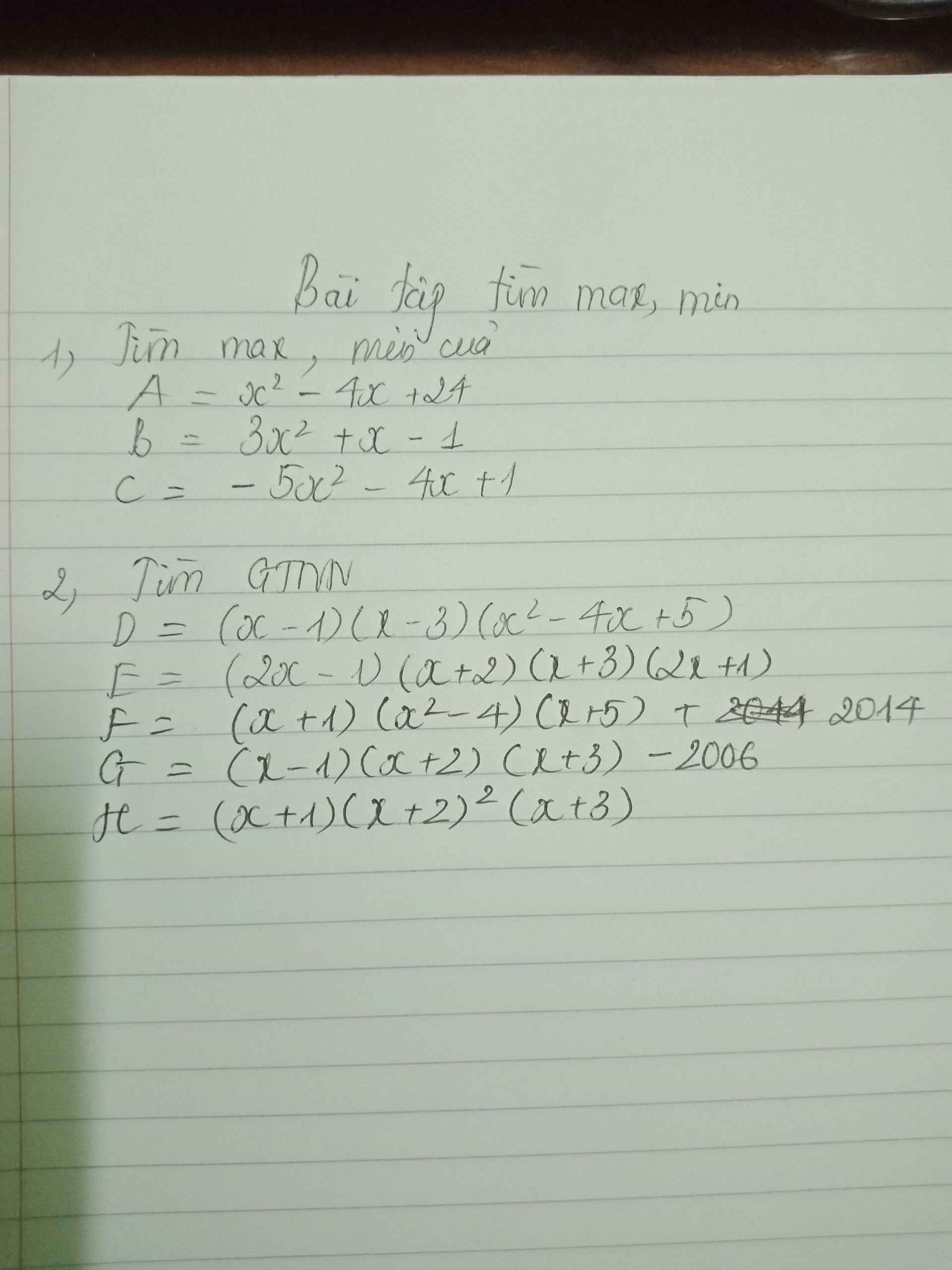xy(x-y)-xz(x+z)yz(2x+y-z)
Violympic toán 8
Hỏi đáp
Bài 2:
a: Ta có: \(A=3x^2+x+2\)
\(=3\left(x^2+\dfrac{1}{3}x+\dfrac{2}{3}\right)\)
\(=3\left(x^2+2\cdot x\cdot\dfrac{1}{6}+\dfrac{1}{36}+\dfrac{23}{36}\right)\)
\(=3\left(x+\dfrac{1}{6}\right)^2+\dfrac{23}{12}\ge\dfrac{23}{12}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{1}{6}\)
Đúng 1
Bình luận (0)
a: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(DN=NC=\dfrac{DC}{2}\)
mà AB=DC
nên AM=MB=DN=NC
Xét tứ giác MBND có
MB//ND
MB=ND
Do đó: MBND là hình bình hành
Suy ra: MD//BN và MD=BN(1)
b: Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Suy ra: I là trung điểm của DM
hay \(IM=\dfrac{DM}{2}\left(2\right)\)
Xét tứ giác BMNC có
BM//NC
BM=NC
Do đó: BMNC là hình bình hành
Suy ra: K là trung điểm của BN
hay \(KN=\dfrac{BN}{2}\left(3\right)\)
Từ (1), (2) và (3) suy ra IM//KN và IM=KN
Xét tứ giác INKM có
IM//KN
IM=KN
Do đó: INKM là hình bình hành
Đúng 1
Bình luận (0)
Cho x+ y = m và x.y = n.Tính giá trị các biểu thức sau theo m,n.
c) x7 + y7
\(x^2+y^2=\left(x+y\right)^2-2xy=m^2-2n\\ x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=m^3-3mn\\ \Rightarrow x^5+y^5=\left(x^3+y^3\right)\left(x^2+y^2\right)-x^2y^2\left(x+y\right)=\left(m^3-3mn\right)\left(m^2-2n\right)-n^2m\\ \Rightarrow x^7+y^7=\left(x^2+y^2\right)\left(x^5+y^5\right)-x^2y^2\left(x^3+y^3\right)=.....\)
Đúng 1
Bình luận (0)
Bài 1: tìm GTLN hoặc GTNN của
a, N=-1-x-x2
b,B=3x2+4x-13
a) \(N=-1-x-x^2=-\left(x^2+x+\dfrac{1}{4}\right)-\dfrac{3}{4}=-\left(x+\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le-\dfrac{3}{4}\)
\(maxN=-\dfrac{3}{4}\Leftrightarrow x=-\dfrac{1}{2}\)
b) \(B=3x^2+4x-13=3\left(x^2+\dfrac{4}{3}x+\dfrac{4}{9}\right)-\dfrac{35}{3}=3\left(x+\dfrac{2}{3}\right)^2-\dfrac{35}{3}\ge-\dfrac{35}{3}\)
\(minB=-\dfrac{35}{3}\Leftrightarrow x=-\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
a: Ta có: \(N=-x^2-x-1\)
\(=-\left(x^2+x+1\right)\)
\(=-\left(x^2+2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\right)\)
\(=-\left(x+\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le-\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{1}{2}\)
b: ta có: \(B=3x^2+4x-13\)
\(=3\left(x^2+\dfrac{4}{3}x-\dfrac{13}{3}\right)\)
\(=3\left(x^2+2\cdot x\cdot\dfrac{2}{3}+\dfrac{4}{9}-\dfrac{43}{9}\right)\)
\(=3\left(x+\dfrac{2}{3}\right)^2-\dfrac{43}{3}\ge-\dfrac{43}{3}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{2}{3}\)
Đúng 0
Bình luận (0)
1:
Ta có: \(A=x^2-4x+24\)
\(=x^2-4x+4+20\)
\(=\left(x-2\right)^2+20\ge20\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 1
Bình luận (0)
1. Tìm max, min
\(A=x^2-4x+24=\left(x-2\right)^2+20\ge20\forall x\)
Dấu "=" xảy ra khi \(x-2=0\Leftrightarrow x=2\)
Vậy \(A_{min}=20\) khi \(x=2\)
\(B=3x^2+x-1=\left(x\sqrt{3}+\dfrac{1}{2\sqrt{3}}\right)^2-\dfrac{13}{12}\ge-\dfrac{13}{12}\forall x\)
Dấu "=" xảy ra khi \(x\sqrt{3}+\dfrac{1}{2\sqrt{3}}=0\Leftrightarrow x=-\dfrac{1}{6}\)
Vậy \(B_{min}=-\dfrac{13}{12}\) khi \(x=-\dfrac{1}{6}\)
\(C=-5x^2-4x+1=-\left(x\sqrt{5}+\dfrac{2}{\sqrt{5}}\right)^2+\dfrac{9}{5}\le\dfrac{9}{5}\forall x\)
Dấu "=" xảy ra khi \(x\sqrt{5}+\dfrac{2}{\sqrt{5}}=0\Leftrightarrow x=-\dfrac{2}{5}\)
Vậy \(C_{max}=\dfrac{9}{5}\) khi \(x=-\dfrac{2}{5}\)
Đúng 1
Bình luận (0)
Tìm x (x-2)(x^2+2x+4)-x(x+3)(x-3)=10
nhanh giùm mình nha vì mình đang cần gấp
\(\left(x-2\right)\left(x^2+2x+4\right)-x\left(x-3\right)\left(x+3\right)=10\\ \Leftrightarrow x^3-8-x\left(x^2-9\right)=10\\ \Leftrightarrow x^3-8-x^3-9x=10\\ \Leftrightarrow-9x=18\\ \Leftrightarrow x=-2\)
Đúng 3
Bình luận (1)
(x−2)(x2+2x+4)−x(x−3)(x+3)=10⇔x3−8−x(x2−9)=10⇔x3−8−x3−9x=10⇔−9x=18⇔x=−2
Đúng 0
Bình luận (0)
Cho tam giác ABC, dựng ra phía ngoài tam giác các hình vuông ABGH và ACEF. Vẽ đường cao AK của tam giác ABC (K ∈ BC), kéo dài AK gặp HF tại I. Chứng minh rằng HI = IF. (Gợi ý: trên tia đối của tia AK lấy điểm P sao cho AP = BC. Sau đó, hãy chứng minh tứ giác HAF P là hình bình hành.
cho tam giác ABC nhọn ,có đường trung tuyến AM.i,k lần lượt là trung điểm của AC và MK.Qua M kẻ đường thẳng song song với ACcắt tia IK tại E.a,CM tứ giácAMEI là hình bình hành
Giải câu đố giúp mình nhé