Giải các phương trình sau:
a) 3 x x + 5 − x + 2 2 = 2 x 2 + 7 ;
b) 4 x + 7 x − 3 − x 2 = 3 x x + 2 + 1 .
Bài 1: Giải các phương trình sau:
a) 3(2,2-0,3x)=2,6 + (0,1x-4)
b) 3,6 -0,5 (2x+1) = x - 0,25(22-4x)
Bài 2: Giải các phương phương trình sau:
a) \(\dfrac{3\left(x-3\right)}{4}\)+\(\dfrac{4x-10,5}{4}\)=\(\dfrac{3\left(x+1\right)}{5}\)+6
b) \(\dfrac{2\left(3x+1\right)+1}{4}\)-5=\(\dfrac{2\left(3x-1\right)}{5}\)-\(\dfrac{3x+2}{10}\)
Mik đang cần gấp nha!!❤
Bài 1: Giải các phương trình sau:
a) 3(2,2-0,3x)=2,6 + (0,1x-4)
<=> 6.6 - 0.9x = 2,6 + 0,1x - 4
<=> - 0.9x - 0,1x = -6.6 -1,4
<=> -x = -8
<=> x = 8
Vậy x = 8
b) 3,6 -0,5 (2x+1) = x - 0,25(22-4x)
<=> 3,6 - x - 0,5 = x - 5,5 + x
<=> - x - 3,1 = -5,5
<=> - x = -2.4
<=> x = 2.4
Vậy x = 2.4
giải các phương trình sau:
a) \(\dfrac{-\left(x^2+5\right)}{x^2-25}=\dfrac{3}{x+5}+\dfrac{x}{x-5}\)
a) ĐKXĐ: \(x\notin\left\{5;-5\right\}\)
Ta có: \(\dfrac{-\left(x^2+5\right)}{x^2-25}=\dfrac{3}{x+5}+\dfrac{x}{x-5}\)
\(\Leftrightarrow\dfrac{3\left(x-5\right)}{\left(x+5\right)\left(x-5\right)}+\dfrac{x\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}=\dfrac{-x^2-5}{\left(x-5\right)\left(x+5\right)}\)
Suy ra: \(3x-15+x^2+5x+x^2+5=0\)
\(\Leftrightarrow2x^2+8x-10=0\)
\(\Leftrightarrow2x^2+10x-2x-10=0\)
\(\Leftrightarrow2x\left(x+5\right)-2\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(2x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=0\\2x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\2x=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\left(loại\right)\\x=1\left(nhận\right)\end{matrix}\right.\)
Vậy: S={1}
`a,(-(x^2+5))/(x^2-25)=3/(x+5)+x/(x-5)`
`ĐK:x ne +-5`
`pt<=>-x^2+5=3(x-5)+x(x+5)`
`<=>-x^2+5=3x-15+x^2+5x`
`<=>-x^2+5=x^2+8x-15`
`<=>2x^2+8x-20=0`
`<=>x^2+4x-5=0`
`<=>x^2-x+5x-5=0`
`<=>x(x-1)+5(x-1)=0`
`<=>` $\left[ \begin{array}{l}x=1\\x=-5\end{array} \right.$
Vậy `S={1,-5}`
giải các phương trình sau:
a)(x+2)(x2-2x+4)-x(x2-2)=15
b)x(x-5)(x+5)-(x+2)(x2-2x+4)=3
\(a,=>x^3-2x^2+4x+2x^2-4x+8-x^3+2x-15=0\)
\(< =>2x-7=0< =>x=\dfrac{7}{2}\)
b,\(=>x\left(x^2-25\right)-\left(x+2\right)\left(x^2-2x+4\right)-3=0\)
\(< =>x^3-25x-x^3+2x^2-4x-2x^2+4x-8-3=0\)
\(< =>-25x-11=0\)
\(< =>x=-0,44\)
Giải các phương trình sau:
a) \(\dfrac{\sqrt{x+1}}{\sqrt{x-5}}=2\)
b) \(\sqrt[3]{x^2-1}=2\)
(a) Điều kiện: \(\left\{{}\begin{matrix}x+1\ge0\\x-5>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x>5\end{matrix}\right.\Rightarrow x>5\).
Phương trình tương đương: \(\sqrt{x+1}=2\sqrt{x-5}\)
\(\Leftrightarrow x+1=4\left(x-5\right)\Leftrightarrow x=7\left(TM\right)\).
Vậy: \(S=\left\{7\right\}.\)
(b) Phương trình tương đương: \(x^2-1=8\)
\(\Leftrightarrow x^2=9\Leftrightarrow x=\pm3\).
Vậy: \(S=\left\{\pm3\right\}\)
a: ĐKXĐ: x+1>=0 và x-5>0
=>x>5
\(\dfrac{\sqrt{x+1}}{\sqrt{x-5}}=2\)
=>\(\sqrt{\dfrac{x+1}{x-5}}=2\)
=>\(\dfrac{x+1}{x-5}=4\)
=>4x-20=x+1
=>3x=21
=>x=7
b: ĐKXĐ: \(x\in R\)
\(\sqrt[3]{x^2-1}=2\)
=>x^2-1=8
=>x^2=9
=>x=3 hoặc x=-3
giải các phương trình sau:
a. x2-25=8(5-x)
b.x-2/ x+2 - 2(x-11)/x2-4 =3/x-2
a.\(x^2-25=8\left(5-x\right)\)
\(\Leftrightarrow\left(x-5\right)\left(x+5\right)-8\left(5-x\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+5\right)+8\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+13\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-13\end{matrix}\right.\)
b.\(\dfrac{x-2}{x+2}-\dfrac{2\left(x-11\right)}{x^2-4}=\dfrac{3}{x-2}\) ; \(ĐK:x\ne\pm2\)
\(\Leftrightarrow\dfrac{\left(x-2\right)\left(x-2\right)-2\left(x-11\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\left(x-2\right)^2-2\left(x-11\right)=3\left(x+2\right)\)
\(\Leftrightarrow x^2-4x+4-2x+22=3x+6\)
\(\Leftrightarrow x^2-9x+20=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
Bài 1. Giải các phương trình sau:
a) |4x2 - 25| = 0
b) |x - 2| = 3
c) |x - 3| = 2x - 1
d) |x - 5| = |3x - 2|
Lời giải:
a) $|4x^2-25|=0$
$\Leftrightarrow 4x^2-25=0$
$\Leftrightarrow (2x-5)(2x+5)=0$
$\Rightarrow x=\pm \frac{5}{2}$
b)
$|x-2|=3$
\(\Rightarrow \left[\begin{matrix} x-2=-3\\ x-2=3\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=-1\\ x=5\end{matrix}\right.\)
c)
\(|x-3|=2x-1\Rightarrow \left\{\begin{matrix} 2x-1\geq 0\\ \left[\begin{matrix} x-3=2x-1\\ x-3=1-2x\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ \left[\begin{matrix} x=-2\\ x=\frac{4}{3}\end{matrix}\right.\end{matrix}\right.\Rightarrow x=\frac{4}{3}\)
d)
$|x-5|=|3x-2|$
\(\Rightarrow \left[\begin{matrix} x-5=3x-2\\ x-5=2-3x\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=\frac{-3}{2}\\ x=\frac{7}{4}\end{matrix}\right.\)
Giải các bất phương trình sau:
a)\(\dfrac{\left(2x-5\right)\left(x+2\right)}{-4x+3}>0\) b)\(\dfrac{x-3}{x+1}=\dfrac{x+5}{x-2}\)
a, \(\dfrac{\left(2x-5\right)\left(x+2\right)}{4x-3}< 0\)
⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}\left(2x-5\right)\left(x+2\right)< 0\\4x-3>0\end{matrix}\right.\\\left\{{}\begin{matrix}\left(2x-5\right)\left(x+2\right)>0\\4x-3< 0\end{matrix}\right.\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}\left\{{}\begin{matrix}-2< x< \dfrac{5}{2}\\x>\dfrac{3}{4}\end{matrix}\right.\\\left\{{}\begin{matrix}\left[{}\begin{matrix}x< -2\\x>\dfrac{5}{2}\end{matrix}\right.\\x< \dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}\dfrac{3}{4}< x< \dfrac{5}{2}\\x< -2\end{matrix}\right.\)
Vậy tập nghiệm của bất phương trình là
S = \(\left(\dfrac{3}{4};\dfrac{5}{2}\right)\cup\left(-\infty;-2\right)\)
b, Pt
⇔ \(\left\{{}\begin{matrix}x^2-5x+6=x^2+6x+5\\x\in R\backslash\left\{-1;2\right\}\end{matrix}\right.\)
⇔ x = \(\dfrac{1}{11}\)
Vậy S = \(\left\{\dfrac{1}{11}\right\}\)
Bài 1. (3 điểm) Giải các phương trình sau:
a) (3x - 7)(x + 5) = (5 + x)(3 - 2x) 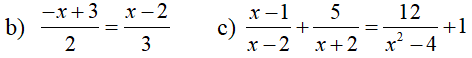
giúp mình với mai thi rồi![]()
\(a,\left(3x-7\right)\left(x+5\right)=\left(5+x\right)\left(3-2x\right)\)
\(\Leftrightarrow\left(3x-7\right)\left(x+5\right)-\left(x+5\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(3x-7-3+2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=0\\5x-10=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=2\end{matrix}\right.\)
\(b,\dfrac{-x+3}{2}=\dfrac{x-2}{3}\left(MSC=6\right)\)
Suy ra :
\(3\left(-x+3\right)=2\left(x-2\right)\)
\(\Leftrightarrow-3x+9-2x+4=0\)
\(\Leftrightarrow-5x+13=0\)
\(\Leftrightarrow x=\dfrac{13}{5}\)
\(c,\dfrac{x-1}{x-2}+\dfrac{5}{x+2}=\dfrac{12}{x^2-4}+1\)\(\left(dkxd:x\ne\pm2\right)\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x+2\right)+5\left(x-2\right)-12-x^2+4}{x^2-4}=0\)
\(\Leftrightarrow x^2+2x-x-2+5x-10-12-x^2+4=0\)
\(\Leftrightarrow6x-20=0\)
\(\Leftrightarrow x=\dfrac{10}{3}\)\(\left(n\right)\)
Vậy \(S=\left\{\dfrac{10}{3}\right\}\)
a | Áp dụng hệ quả của định lý Ta-lét ta có: 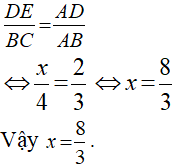 |
b | Ta có: 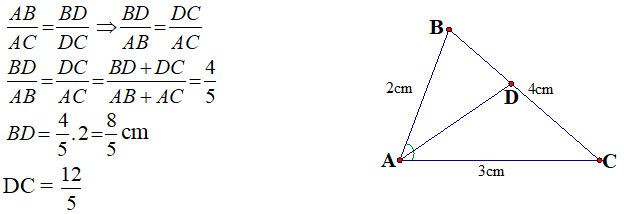 |
giải các phương trình sau:
a) \(3x^2-17x+24=\sqrt{x-3}+3\sqrt{5-x}\)
b) \(\sqrt[3]{x+6}-2\sqrt{x-1}=4-x^2\)
giải các phương trình sau:
a) \(x^2+4x+5=2\sqrt{2x+3}\).
b) \(3x^2+2x=2\sqrt{x^2+x}+1-x\).
\(a,\Leftrightarrow x^2+2x+1+2x+3-2\sqrt{2x+3}+1=0\\ \Leftrightarrow\left(x+1\right)^2+\left(\sqrt{2x+3}-1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=-1\\2x+3=1\end{matrix}\right.\Leftrightarrow x=-1\left(N\right)\)
\(b,\Leftrightarrow3x^2+3x-2\sqrt{x^2+x}=0\left(x\le-1;x\ge0\right)\\ \Leftrightarrow3x\left(x-1\right)-2\sqrt{x\left(x+1\right)}=0\\ \Leftrightarrow\sqrt{x\left(x+1\right)}\left(3\sqrt{x\left(x-1\right)}-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x\left(x-1\right)=0\\\sqrt{x\left(x-1\right)}=\dfrac{2}{3}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x^2-x-\dfrac{4}{9}=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\9x^2-9x-4=0\left(1\right)\end{matrix}\right.\)
\(\Delta\left(1\right)=81-4\left(-4\right)\cdot9=225\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=\dfrac{9-15}{18}\\x=\dfrac{9+15}{18}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(N\right)\\x=1\left(N\right)\\x=-\dfrac{1}{3}\left(L\right)\\x=\dfrac{4}{3}\left(N\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=\dfrac{4}{3}\end{matrix}\right.\)