Giải các phương trình sau
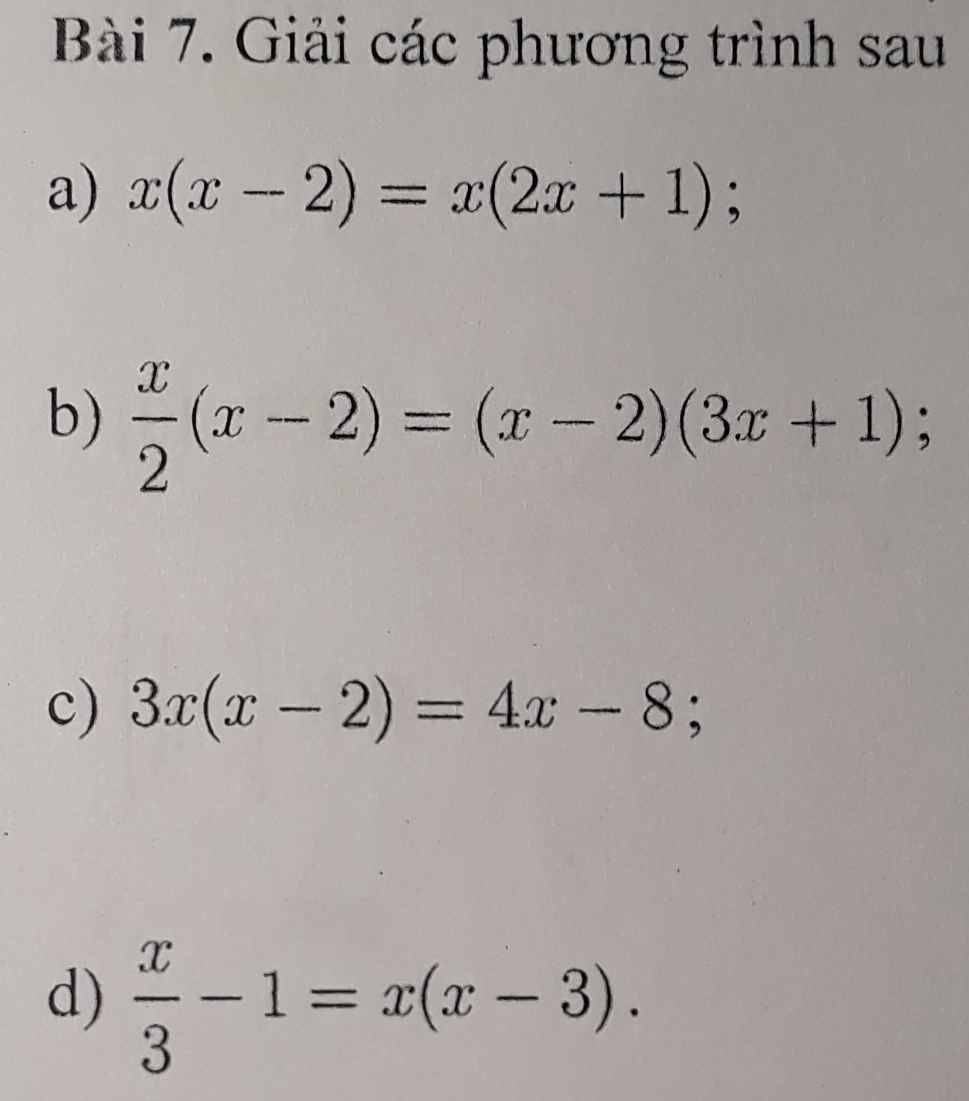
Giải các phương trình sau
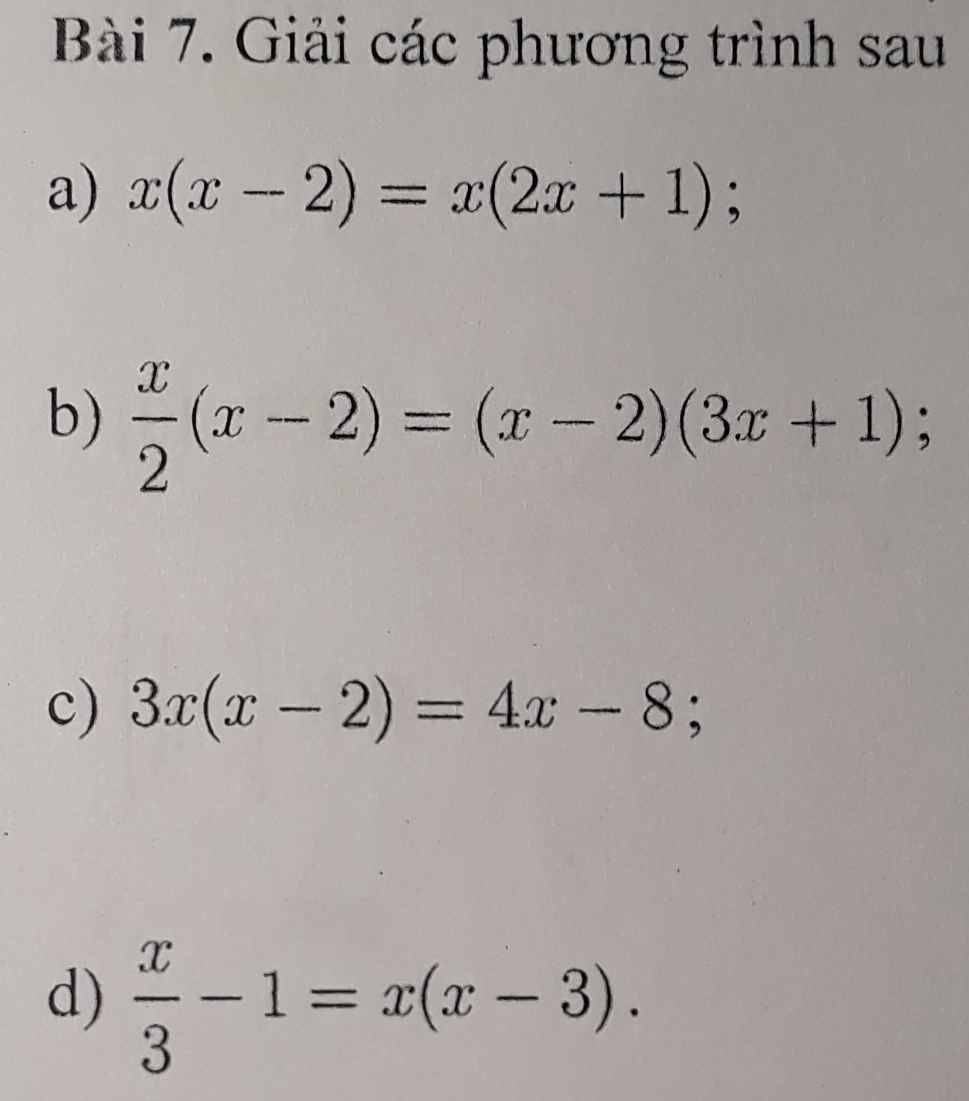
a/\(x\left(x-2\right)=x\left(2x+1\right)\)
\(\Rightarrow x^2-2x=2x^2+x\)
\(\Rightarrow x^2-2x^2=x+2x\)
\(\Rightarrow-x^2=3x\)
\(\Rightarrow-x^2-3x=0\)
\(\Rightarrow x\left(-x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)
Vậy...
b/\(\dfrac{x}{2}\left(x-2\right)=\left(x-2\right)\left(3x+1\right)\)
\(\Rightarrow\dfrac{x^2}{2}-x=3x^2+x-6x-2\)
\(\Rightarrow\dfrac{x^2}{2}-x=3x^2-5x-2\)
\(\Rightarrow\dfrac{x^2}{2}-3x^2=-5x+x-2\)
\(\Rightarrow-\dfrac{5}{2}x^2=-4x-2\)
\(\Rightarrow-\dfrac{5}{2}x^2+4x+2=0\)
\(\Rightarrow5x^2-8x-4=0\)
\(\Rightarrow\left(5x^2-10x\right)+\left(2x-4\right)=0\)
\(\Rightarrow5x\left(x-2\right)+2\left(x-2\right)=0\)
\(\Rightarrow\left(x-2\right)\left(5x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{2}{5}\end{matrix}\right.\)
Vậy...
c/\(3x\left(x-2\right)=4x-8\)
\(\Rightarrow3x^2-6x=4x-8\)
\(\Rightarrow-6x+3x^2=4x-8\)
\(\Rightarrow-6x-4x=-8-3x^2\)
\(\Rightarrow-10x=-8-3x^2\)
\(\Rightarrow-10x+8+3x^2=0\)
\(\Rightarrow3x^2-10x+8=0\)
\(\Rightarrow\left(3x^2-4x\right)-\left(6x-8\right)=0\)
\(\Rightarrow x\left(3x-4\right)-2\left(3x-4\right)=0\)
\(\Rightarrow\left(3x-4\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=2\end{matrix}\right.\)
Vậy...
d/\(\dfrac{x}{3}-1=x\left(x-3\right)\)
\(\Rightarrow\dfrac{x}{3}-1=x^2-3x\)
\(\Rightarrow-1+\dfrac{x}{3}=x^2-3x\)
\(\Rightarrow-1-x^2=-3x-\dfrac{x}{3}\)
\(\Rightarrow-1-x^2=-\dfrac{10}{3}x\)
\(\Rightarrow-1-x^2+\dfrac{10}{3}x=0\)
\(\Rightarrow-x^2+\dfrac{10}{3}x-1=0\)
\(\Rightarrow3x^2-10x+3=0\)
\(\Rightarrow\left(3x^2-x\right)-\left(9x-3\right)=0\)
\(\Rightarrow x\left(3x-1\right)-3\left(3x-1\right)=0\)
\(\Rightarrow\left(3x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=3\end{matrix}\right.\)
Vậy
#kễnh
một người đi xe máy từ a đến b với vận tốc trung bình 40km/h .khi đi được 2/3 quãng đường, bạn tăng lên 5km/h.Tính quãng đường từ nhà đến trường biết thời gian bạn ấy đi là28 phút
(2y-3)(y+1)+y(y-2)=3(y+2)^2
(2y - 3)(y + 1) + y(y - 2) = 3(y + 2)²
⇔ 2y² + 2y - 3y - 3 + y² - 2y = 3(y² + 4y + 4)
⇔ 3y² - 3y - 3 = 3y² + 12y + 12
⇔ 3y² -3y - 3y² -12y = 12 + 3
⇔ -15y = 15
⇔ y = -1
Vậy S = {-1}
\(\left(2y-3\right).\left(y+1\right)+y.\left(y+2\right)=3\left(y+2\right)^2\\ \Leftrightarrow2y^2-y-3+y^2+2y=3y^2+12y+12\\ \Leftrightarrow3y^2-2y^2-y^2+12y-2y+y=-3-12\\ \Leftrightarrow11y=-15\\ \Leftrightarrow y=-\dfrac{15}{11}\\ Vậy:S=\left\{-\dfrac{15}{11}\right\}\)
Giải phương trình sau: a)x^2 -3x +2= 0 b) |2x| = 3x +2 c)|-2x| = 3x+4 Các bạn ai biết giúp mk vs mk cảm ơn
a: =>(x-1)(x-2)=0
=>x=1 hoặc x=2
b: TH1: x>=0
=>2x=3x+2
=>x=-2(loại)
TH2: x<0
=>-2x=3x+2
=>-5x=2
=>x=-2/5(nhận)
c: TH1: x>=0
=>2x=3x+4
=>-x=4
=>x=-4(loại)
TH2: x<0
=>-2x=3x+4
=>-5x=4
=>x=-4/5(nhận)
Nghiệm của bất phương trình x^2 _>0 là {x|x€R} vì sao?
Bài 3: a) Một người đi xe máy từ 4 đến B với vận tốc 25km/h. Lúc về người đó đi với vận tốc 30km/h, nên thời gian về ít hơn thời gian đi là 20 phút. Tỉnh AB ? b) Một người đi xe đạp từ A đến B với vận tốc 15 km/h. Sau đó quay về tử B về A với vận tốc 12 km/h. Cả đi lẫn về hết 4 giờ 30 phút. Tính quãng đường 4B
a)đổi 20h=1/3 h
tg đi là x/25
tg lúc về là x/30
theo bài ra ta có pt
x/25-x/30=1/3
<=>x.30/750-x.25/750=1.250/750
<=>30x-25x=250
<=>5x=250
<=>x=250:5
<=>x=50
vậy quãng đường AB là 50 km![]()
b: Gọi độ dài AB là x
Thời gian đi là x/15
Thời gian về là x/12
Theo đề, ta có: x/15+x/12=4,5
=>x=30
Bàil: Giải phương trình sau a) 2x - 3 = 3 - x b) 7x - 4 = 3x + 12 c) 3x - 6 + x = 9 - x d) 10x - 12 - 3x = 6 + x Bài 2: Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số: a) 4x + 6 <= 2x - 2 b) 3x + 15 < 0 c) 3x - 3 > x + 5 d) x - 4 > - 2x + 5 Bài3: a) Một người đi xe máy từ 4 đến B với vận tốc 25km/h. Lúc về người đó đi với vận tốc 30km/h, nên thời gian về ít hơn thời gian đi là 20 phút. Tính AB ? b) Một người đi xe đạp từ A đến B với vận tốc 15 km/h. Sau đó quay về từ B về A với vận tốc 12 km/h. Cả đi lẫn về hết 4 giờ 30 phút. Tính quãng đường 4B Bài 4: Cho tam giác ABC vuông tại A với AB = 3cm AC= 4cm vẽ đường cao AE. a) Chứng minh rằng AABC đồng dạng với AEBA. b) Tia phân giác của góc ABC cắt AC tại F. Tính BF Bài 5: Cho tam giác ABC có AC = 8cm, AC = 16cm Gọi D và E là hai điểm lần lượt trên cạnh AB và AC sao cho BD = 2cm CE = 13cm Chứng minh rằng a. AAEB AADC b. AED= ABC, cho DE = 5cm Tính BC? C. AE AC AD AB
1:
a: =>3x=6
=>x=2
b: =>4x=16
=>x=4
c: =>4x-6=9-x
=>5x=15
=>x=3
d: =>7x-12=x+6
=>6x=18
=>x=3
2:
a: =>2x<=-8
=>x<=-4
b: =>x+5<0
=>x<-5
c: =>2x>8
=>x>4
cho a^2 + b^2 < 2 . Chứng minh a+b<2
a^2+b^2<2
=>a^2<2-b^2
=>\(a< \sqrt{2-b^2}< =2-b\)
=>a+b<=2
 Giải hộ e bài này ạ
Giải hộ e bài này ạ
Tổng tiền mua cây bút và hộp bút:
4000 x 5 + 50000 = 70000(đồng)
Số tiền còn lại:
250000 - 70000= 180000(đồng)
Nam có thể mua được nhiều nhất số quyển vở là:
180000: 8000 = 22 (quyển) (Thừa 4000 đồng)
cho a, b, c thỏa mãn a+b+c=2, ab+bc+ac=1. Chứng minh 4/3 >= a,bb,c >=0