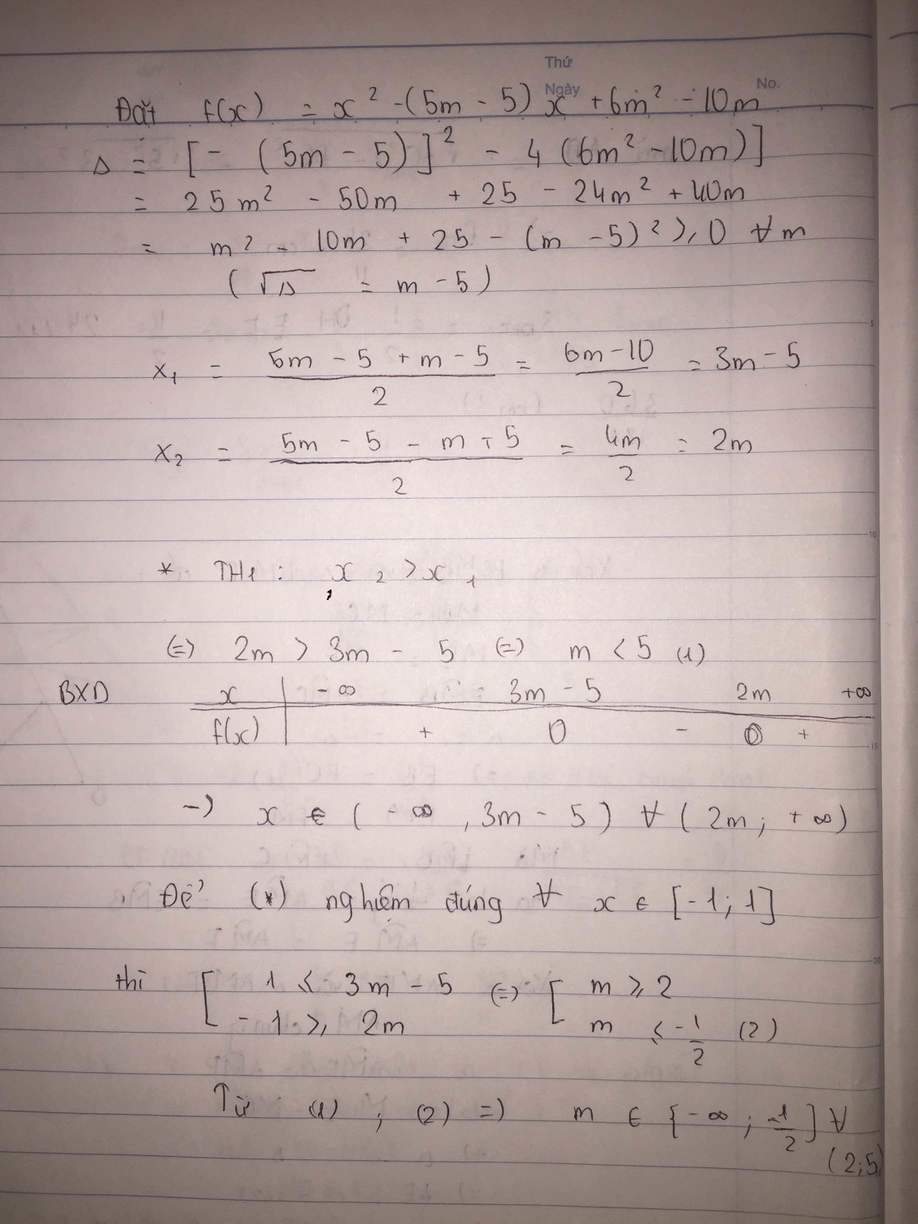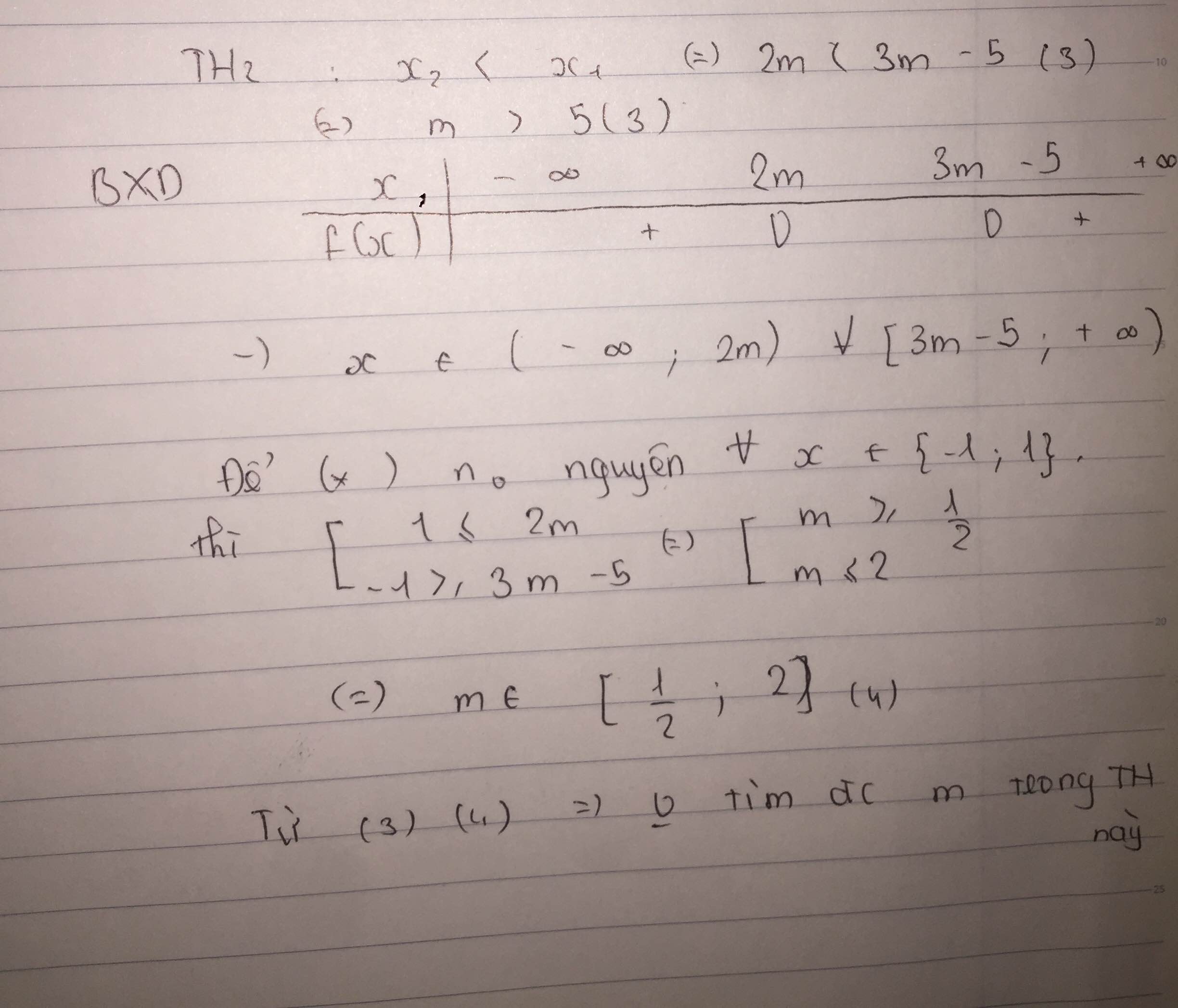1.

\(2\left|x-m\right|+x^2+2>2mx\)

\(\Leftrightarrow\left(x-m\right)^2+2\left|x-m\right|-m^2+2>0\)

\(\Leftrightarrow t^2+2t-m^2+2>0\left(t=\left|x-m\right|\ge0\right)\)

\(\Leftrightarrow m^2< f\left(t\right)=t^2+2t+2\)

Yêu cầu bài toán thỏa mãn khi \(m^2< minf\left(t\right)=2\)

\(\Leftrightarrow-\sqrt{2}< m< 2\)

Vậy \(-\sqrt{2}< m< 2\)

2.

\(x^2+2\left|x+m\right|+2mx+3m^2-3m+1< 0\)

\(\Leftrightarrow\left(x+m\right)^2+2\left|x+m\right|+2m^2-3m+1< 0\)

\(\Leftrightarrow\left(\left|x+m\right|+1\right)^2< -2m^2+3m\)

Ta có \(VT=\left(\left|x+m\right|+1\right)^2=\left(-\left|x+m\right|-1\right)^2\le\left(-1\right)^2=1\)

Yêu cầu bài toán thỏa mãn khi \(VP=-2m^2+3m>1\)

\(\Leftrightarrow2m^2-3m+1< 0\)

\(\Leftrightarrow\dfrac{1}{2}< m< 1\)

TH1: m=-1

=>x-2>0

=>x>2(loại)

TH2: m<>-1

Δ=(-2m)^2-4*2m*(m+1)

=4m^2-8m^2-8m

=-4m^2-8m

Để BPT luôn có nghiệm thì -4m^2-8m<0 và m+1>0

=>4m^2+8m>0 và m>-1

=>4m(m+2)>0 và m>-1

=>m>0

\(\Leftrightarrow\sqrt{-x^2-2x+15}\le x^2+2x+m\)

\(\Leftrightarrow-x^2-2x+15+\sqrt{-x^2-2x+15}-15\le m\)

Đặt \(t=-x^2-2x+15\Rightarrow0\le t\le4\)

\(\Rightarrow t^2+t-15\le m\) với \(t\in\left[0;4\right]\)

\(\Leftrightarrow m\ge\max\limits_{\left[0;4\right]}\left(t^2+t-15\right)\)

Xét \(f\left(t\right)=t^2+t-15\) trên [0;4]

\(-\dfrac{b}{2a}=-\dfrac{1}{2}\notin\left[0;4\right]\) ; \(f\left(0\right)=-15\) ; \(f\left(4\right)=5\)

\(\Rightarrow f\left(t\right)\le5\Rightarrow m\ge5\)

\(ycđb\Leftrightarrow\left[{}\begin{matrix}\Delta\le0\Leftrightarrow\left(m-5\right)^2\le0\Leftrightarrow m=5\\1\le x1< x2\left(1\right)\\x1< x2\le-1\left(2\right)\end{matrix}\right.\)

\(\Delta>0\Leftrightarrow\left(m-5\right)^2>0\Leftrightarrow m\ne5\)

\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\left(x1-1\right)\left(x2-1\right)\ge0\\x1+x2-2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x1x2-\left(x1+x2\right)+1\ge0\\5m-5-2>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}6m^2-10m-\left(5m-5\right)+1\ge0\\m>\dfrac{7}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m\le\dfrac{1}{2}\\m\ge2\end{matrix}\right.\\m>\dfrac{7}{5}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}m\ge2\\m\ne5\end{matrix}\right.\)

\(\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}\left(x1+1\right)\left(x2+1\right)\ge0\\x1+x2+2< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x1x2+x1+x2+1\ge0\\x1+x2+2< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}6m^2-10m+5m-5+1\ge0\\5m-5-2< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m\le-\dfrac{1}{2}\\m\ge\dfrac{4}{3}\end{matrix}\right.\\m< \dfrac{7}{5}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}m\in[\dfrac{4}{3};\dfrac{7}{5})\\m\le-\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow\)\(m\in(-\infty;-\dfrac{1}{2}]\cup[\dfrac{4}{3};\dfrac{7}{5})\cup[2;+\infty)\cup\left\{5\right\}\)

\(f\left(x\right)=x^2-2\left(m-1\right)x+m-2\)

Yêu cầu bài toán thõa mãn khi \(f\left(x\right)=0\) có hai nghiệm thỏa mãn \(x_1\le1< 3\le x_2\)

\(\left\{{}\begin{matrix}\Delta'=m^2-3m+3\ge0\\f\left(1\right)\le0\\f\left(3\right)\le0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\in R\\-m+1\le0\\15-5m\le0\end{matrix}\right.\)

\(\Leftrightarrow m\ge3\)

\(\Delta'=m^2-2m+3>0\) ; \(\forall x\)

Do đó bài toán thỏa mãn khi pt \(f\left(x\right)=0\) có 2 nghiệm thỏa mãn: \(x_1< -1< 2< x_2\)

\(\Leftrightarrow\left\{{}\begin{matrix}a.f\left(-1\right)< 0\\a.f\left(2\right)< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}1.\left(1-2m+2m-3\right)< 0\\1\left(4+4m+2m-3\right)< 0\end{matrix}\right.\)

\(\Leftrightarrow6m+1< 0\Rightarrow m< -\dfrac{1}{6}\)

Em kiểm tra lại tử số của đề bài

1.a.

\(\left(x+1\right)\left(x+2\right)\left(x-2\right)\left(x+5\right)\ge m\)

\(\Leftrightarrow\left(x^2+3x+2\right)\left(x^2+3x-10\right)\ge m\)

Đặt \(x^2+3x-10=t\ge-\dfrac{49}{4}\)

\(\Rightarrow\left(t+2\right)t\ge m\Leftrightarrow t^2+2t\ge m\)

Xét \(f\left(t\right)=t^2+2t\) với \(t\ge-\dfrac{49}{4}\)

\(-\dfrac{b}{2a}=-1\) ; \(f\left(-1\right)=-1\) ; \(f\left(-\dfrac{49}{4}\right)=\dfrac{2009}{16}\)

\(\Rightarrow f\left(t\right)\ge-1\)

\(\Rightarrow\) BPT đúng với mọi x khi \(m\le-1\)

Có 30 giá trị nguyên của m

1b.

Với \(x=0\)  BPT luôn đúng

Với \(x\ne0\) BPT tương đương:

\(\dfrac{\left(x^2-2x+4\right)\left(x^2+3x+4\right)}{x^2}\ge m\)

\(\Leftrightarrow\left(x+\dfrac{4}{x}-2\right)\left(x+\dfrac{4}{x}+3\right)\ge m\)

Đặt \(x+\dfrac{4}{x}-2=t\) \(\Rightarrow\left[{}\begin{matrix}t\ge2\\t\le-6\end{matrix}\right.\)

\(\Rightarrow t\left(t+5\right)\ge m\Leftrightarrow t^2+5t\ge m\)

Xét hàm \(f\left(t\right)=t^2+5t\) trên \(D=(-\infty;-6]\cup[2;+\infty)\)

\(-\dfrac{b}{2a}=-\dfrac{5}{2}\notin D\) ; \(f\left(-6\right)=6\) ; \(f\left(2\right)=14\)

\(\Rightarrow f\left(t\right)\ge6\)

\(\Rightarrow m\le6\)

Vậy có 37 giá trị nguyên của m thỏa mãn

2.

Xét với \(x\ge1\)

\(m\left(x+1\right)+3\left(x-1\right)-2\sqrt{x^2-1}=0\)

\(\Leftrightarrow m+3\left(\dfrac{x-1}{x+1}\right)-2\sqrt{\dfrac{x-1}{x+1}}=0\)

Đặt \(\sqrt{\dfrac{x-1}{x+1}}=t\Rightarrow0\le t< 1\)

\(\Rightarrow m+3t^2-2t=0\)

\(\Leftrightarrow3t^2-2t=-m\)

Xét hàm \(f\left(t\right)=3t^2-2t\) trên \(D=[0;1)\)

\(-\dfrac{b}{2a}=\dfrac{1}{3}\in D\) ; \(f\left(0\right)=0\) ; \(f\left(\dfrac{1}{3}\right)=-\dfrac{1}{3}\) ; \(f\left(1\right)=1\)

\(\Rightarrow-\dfrac{1}{3}\le f\left(t\right)< 1\)

\(\Rightarrow\) Pt có nghiệm khi \(-\dfrac{1}{3}\le-m< 1\)

\(\Leftrightarrow-1< m\le\dfrac{1}{3}\)