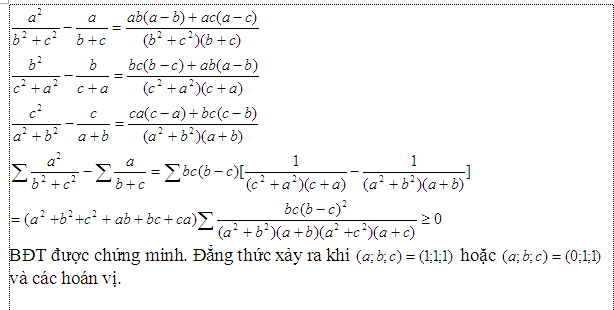3/ Áp dụng bất đẳng thức AM-GM, ta có :

\(\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}\ge2\sqrt{\dfrac{\left(ab\right)^2}{\left(bc\right)^2}}=\dfrac{2a}{c}\)

\(\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge2\sqrt{\dfrac{\left(bc\right)^2}{\left(ac\right)^2}}=\dfrac{2b}{a}\)

\(\dfrac{c^2}{a^2}+\dfrac{a^2}{b^2}\ge2\sqrt{\dfrac{\left(ac\right)^2}{\left(ab\right)^2}}=\dfrac{2c}{b}\)

Cộng 3 vế của BĐT trên ta có :

\(2\left(\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\right)\ge2\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)\)

\(\Leftrightarrow\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\left(\text{đpcm}\right)\)

Bài 1:

Áp dụng BĐT AM-GM ta có:

\(\frac{1}{a^2+bc}+\frac{1}{b^2+ac}+\frac{1}{c^2+ab}\leq \frac{1}{2\sqrt{a^2.bc}}+\frac{1}{2\sqrt{b^2.ac}}+\frac{1}{2\sqrt{c^2.ab}}=\frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}{2abc}\)

Tiếp tục áp dụng BĐT AM-GM:

\(\sqrt{bc}+\sqrt{ac}+\sqrt{ab}\leq \frac{b+c}{2}+\frac{c+a}{2}+\frac{a+b}{2}=a+b+c\)

Do đó:

\(\frac{1}{a^2+bc}+\frac{1}{b^2+ac}+\frac{1}{c^2+ab}\leq \frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}{2abc}\leq \frac{a+b+c}{2abc}\) (đpcm)

Dấu "=" xảy ra khi $a=b=c$

Bài 2:

Thay $1=a+b+c$ và áp dụng BĐT AM-GM ta có:

\(\left(1+\frac{1}{a}\right)\left(1+\frac{1}{b}\right)\left(1+\frac{1}{c}\right)=\frac{(a+1)(b+1)(c+1)}{abc}\)

\(=\frac{(a+a+b+c)(b+a+b+c)(c+a+b+c)}{abc}\)

\(\geq \frac{4\sqrt[4]{a.a.b.c}.4\sqrt[4]{b.a.b.c}.4\sqrt[4]{c.a.b.c}}{abc}=\frac{64abc}{abc}=64\)

Ta có đpcm
Dấu "=" xảy ra khi $a=b=c=\frac{1}{3}$

2: Ta có: \(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}=\dfrac{a\left(a+b+c\right)}{b+c}+\dfrac{b\left(a+b+c\right)}{c+a}+\dfrac{c\left(a+b+c\right)}{a+b}-a-b-c=\left(a+b+c\right)\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)=a+b+c-a-b-c=0\)

1: Sửa đề: Cho \(x,y,z\ne0\) và \(\dfrac{1}{x}+\dfrac{2}{y}+\dfrac{1}{z}=\dfrac{2}{2x+y+2z}\).

CM:....

Đặt 2x = x', 2z = z'.

Ta có: \(\dfrac{2}{x'}+\dfrac{2}{y}+\dfrac{2}{z'}=\dfrac{2}{x'+y+z'}\)

\(\Leftrightarrow\dfrac{1}{x'}+\dfrac{1}{y}+\dfrac{1}{z'}=\dfrac{1}{x'+y+z'}\)

\(\Leftrightarrow\dfrac{1}{x'}-\dfrac{1}{x'+y+z'}+\dfrac{1}{y}+\dfrac{1}{z'}=0\)

\(\Leftrightarrow\dfrac{y+z'}{x'\left(x'+y+z'\right)}+\dfrac{y+z'}{yz'}=0\)

\(\Leftrightarrow\dfrac{\left(y+z'\right)\left(yz'+x'^2+x'y+x'z'\right)}{x'yz'\left(x'+y+z'\right)}=0\)

\(\Leftrightarrow\dfrac{\left(x'+y\right)\left(y+z'\right)\left(z'+x'\right)}{x'yz'\left(x'+y+z'\right)}=0\Leftrightarrow\left(2x+y\right)\left(y+2z\right)\left(2z+2x\right)=0\Leftrightarrow\left(2x+y\right)\left(y+2z\right)\left(z+x\right)=0\left(đpcm\right)\)

1.

 Áp dụng BĐT BSC:

\(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge\dfrac{\left(a+b+c\right)^2}{2\left(a+b+c\right)}=\dfrac{a+b+c}{2}\)

Đẳng thức xảy ra khi \(a=b=c>0\)

2.

Áp dụng BĐT \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\) và BĐT BSC:

\(\dfrac{a+b}{a^2+b^2}+\dfrac{b+c}{b^2+c^2}+\dfrac{c+a}{c^2+a^2}\)

\(\le\dfrac{a+b}{\dfrac{\left(a+b\right)^2}{2}}+\dfrac{b+c}{\dfrac{\left(b+c\right)^2}{2}}+\dfrac{c+a}{\dfrac{\left(c+a\right)^2}{2}}\)

\(=\dfrac{2}{a+b}+\dfrac{2}{b+c}+\dfrac{2}{c+a}\)

\(\le2.\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}+\dfrac{1}{a}\right)\)

\(=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)

Đẳng thức xảy ra khi \(a=b=c>0\)

Cách khác:

1.

 Áp dụng BĐT Cauchy:

\(\dfrac{a^2}{b+c}+\dfrac{b+c}{4}+\dfrac{b^2}{c+a}+\dfrac{c+a}{4}+\dfrac{c^2}{a+b}+\dfrac{a+b}{4}\ge a+b+c\)

\(\Leftrightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge a+b+c-\dfrac{a+b+c}{2}=\dfrac{a+b+c}{2}\)

Đẳng thức xảy ra khi \(a=b=c>0\)

a, Từ \(\dfrac{a}{c}=\dfrac{c}{b}\Rightarrow c^2=a\cdot b\). Khi đó :

\(\dfrac{a^2+c^2}{b^2+c^2}=\dfrac{a^2+a\cdot b}{b^2+a\cdot b}=\dfrac{a\cdot\left(a+b\right)}{b\cdot\left(a+b\right)}=\dfrac{a}{b}=VP\)

⇒ĐPCM

b, Từ \(\dfrac{a}{c}=\dfrac{c}{b}\Rightarrow c^2=a\cdot b\) và áp dụng công thức \(a^2-b^2=\left(a+b\right)\cdot\left(a-b\right)\).Khi đó :

\(\dfrac{b^2-a^2}{a^2+c^2}=\dfrac{\left(b-a\right)\left(b+a\right)}{a^2+a\cdot b}=\dfrac{\left(b-a\right)\left(a+b\right)}{a\cdot\left(a+b\right)}=\dfrac{b-a}{a}=VP\)

⇒ĐPCM

Áp dụng bđt Cô-si:

\(\dfrac{a^2}{b+c}+\dfrac{b+c}{4}\ge2\sqrt{\dfrac{a^2}{b+c}\cdot\dfrac{\left(b+c\right)}{4}}=2\sqrt{\dfrac{a^2}{4}}=a\)

Chứng minh tương tự :

\(\dfrac{b^2}{c+a}+\dfrac{c+a}{4}\ge b;\dfrac{c^2}{a+b}+\dfrac{a+b}{4}\ge c\)

\(\Rightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}+\dfrac{1}{4}\left(2a+2b+2c\right)\ge a+b+c\Rightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge a+b+c-\dfrac{1}{2}\left(a+b+c\right)=\dfrac{a+b+c}{2}\) Dấu= xảy ra \(\Leftrightarrow a=b=c\)

\(\dfrac{a+b}{ab+c^2}=\dfrac{\left(a+b\right)^2}{\left(ab+c^2\right)\left(a+b\right)}=\dfrac{\left(a+b\right)^2}{b\left(a^2+c^2\right)+a\left(b^2+c^2\right)}\le\dfrac{a^2}{b\left(a^2+c^2\right)}+\dfrac{b^2}{a\left(b^2+c^2\right)}\)

Tương tự: 

\(\dfrac{b+c}{bc+a^2}\le\dfrac{b^2}{c\left(a^2+b^2\right)}+\dfrac{c^2}{b\left(a^2+c^2\right)}\) ; \(\dfrac{c+a}{ca+b^2}\le\dfrac{c^2}{a\left(b^2+c^2\right)}+\dfrac{a^2}{c\left(a^2+b^2\right)}\)

Cộng vế:

\(VT\le\dfrac{1}{a}\left(\dfrac{b^2}{b^2+c^2}+\dfrac{c^2}{b^2+c^2}\right)+\dfrac{1}{b}\left(\dfrac{a^2}{a^2+c^2}+\dfrac{c^2}{a^2+c^2}\right)+\dfrac{1}{c}\left(\dfrac{a^2}{a^2+b^2}+\dfrac{b^2}{a^2+b^2}\right)=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)