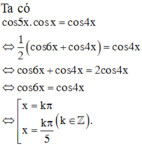a/ \(cos\left(x+15^0\right)=1\Leftrightarrow x+15^0=k360^0\Rightarrow x=-15^0+k360^0\)

b/ \(cos\left(3x+\frac{\pi}{3}\right)=\frac{\sqrt{2}}{2}\Rightarrow\left[{}\begin{matrix}3x+\frac{\pi}{3}=\frac{\pi}{4}+k2\pi\\3x+\frac{\pi}{3}=-\frac{\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{36}+\frac{k2\pi}{3}\\x=-\frac{7\pi}{36}+\frac{k2\pi}{3}\end{matrix}\right.\)

c/ \(cos\left(4x-\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{3}\Rightarrow cos\left(4x-\frac{\pi}{4}\right)=cosa\)

\(\Rightarrow\left[{}\begin{matrix}4x-\frac{\pi}{4}=a+k2\pi\\4x-\frac{\pi}{4}=-a+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{16}+\frac{a}{4}+\frac{k\pi}{2}\\x=\frac{\pi}{16}-\frac{a}{4}+\frac{k\pi}{2}\end{matrix}\right.\)

d/ \(cos4x=cos\left(x+\frac{\pi}{3}\right)\Rightarrow\left[{}\begin{matrix}x+\frac{\pi}{3}=4x+k2\pi\\x+\frac{\pi}{3}=-4x+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{9}+\frac{k2\pi}{3}\\x=-\frac{\pi}{15}+\frac{k2\pi}{5}\end{matrix}\right.\)

e/ \(cos5x=-cos3x=cos\left(\pi-3x\right)\Rightarrow\left[{}\begin{matrix}5x=\pi-3x+k2\pi\\5x=3x-\pi+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{8}+\frac{k\pi}{4}\\x=-\frac{\pi}{2}+k\pi\end{matrix}\right.\)

Đáp án A

Vậy phương trình có nghiệm là

a) \(\left(sinx+cosx\right)^2=sin^2x+2sinxcosx+cos^2x\)\(=1+2sinxcosx\).
b) \(\left(sinx-cosx\right)^2=sin^2x-2sinxcosx+cos^2x\)\(=1-2sinxcosx\).
c) \(sin^4x+cos^4x=\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x\)
\(=1-2sin^2xcos^2x\).

5.

\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=\frac{5}{6}\left[\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\right]\)

\(\Leftrightarrow1-3sin^2x.cos^2x=\frac{5}{6}\left(1-2sin^2x.cos^2x\right)\)

\(\Leftrightarrow1-\frac{3}{4}sin^22x=\frac{5}{6}\left(1-\frac{1}{2}sin^22x\right)\)

\(\Leftrightarrow\frac{1}{3}sin^22x=\frac{1}{6}\)

\(\Leftrightarrow sin^22x=\frac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}sin2x=\frac{\sqrt{2}}{2}\\sin2x=-\frac{\sqrt{2}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{8}+k\pi\\x=\frac{3\pi}{8}+k\pi\\x=-\frac{\pi}{8}+k\pi\\x=\frac{5\pi}{8}+k\pi\end{matrix}\right.\)

6.

\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)+\frac{1}{2}sinx.cosx=0\)

\(\Leftrightarrow1-3sin^2x.cos^2x+\frac{1}{2}sinx.cosx=0\)

\(\Leftrightarrow1-\frac{3}{4}sin^22x+\frac{1}{4}sin2x=0\)

\(\Leftrightarrow-3sin^22x+sin2x+4=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sin2x=-1\\sin2x=\frac{4}{3}>1\left(l\right)\end{matrix}\right.\)

\(\Rightarrow2x=-\frac{\pi}{2}+k2\pi\)

\(\Rightarrow x=-\frac{\pi}{4}+k\pi\)

1.

\(\Rightarrow4cos^3x.cos3x+4sin^3x.sin3x=\sqrt{2}\)

\(\Leftrightarrow\left(3cosx+cos3x\right)cos3x+\left(3sinx-sin3x\right)sin3x=\sqrt{2}\)

\(\Leftrightarrow3\left(cos3x.cosx+sin3x.sinx\right)+cos^23x-sin^23x=\sqrt{2}\)

\(\Leftrightarrow3cos2x+cos6x=\sqrt{2}\)

\(\Leftrightarrow3cos2x+4cos^32x-3cos2x=\sqrt{2}\)

\(\Leftrightarrow4cos^32x=\sqrt{2}\)

\(\Leftrightarrow cos2x=\frac{\sqrt{2}}{2}\)

\(\Rightarrow\left[{}\begin{matrix}2x=\frac{\pi}{4}+k2\pi\\2x=-\frac{\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{8}+k\pi\\x=-\frac{\pi}{8}+k\pi\end{matrix}\right.\)

\(VT=\sin5x-2\sin x\cdot\cos4x-2\sin x\cdot\cos2x\)

\(=\sin5x-\left(\sin5x-\sin3x\right)-\left(\sin3x-\sin x\right)\)

\(=\sin5x-\sin5x+\sin3x-\sin3x+\sin x\)

\(=\sin x=VP\)

a.

Tổng là cấp số nhân lùi vô hạn với \(\left\{{}\begin{matrix}u_1=1\\q=-sin^2x\end{matrix}\right.\)

Do đó: \(S=\dfrac{u_1}{1-q}=\dfrac{1}{1+sin^2x}\)

b. Tương tự, tổng cấp số nhân lùi vô hạn với \(\left\{{}\begin{matrix}u_1=1\\q=cos^2x\end{matrix}\right.\)

\(\Rightarrow S=\dfrac{1}{1-cos^2x}=\dfrac{1}{sin^2x}\)

c. Do \(0< x< \dfrac{\pi}{4}\Rightarrow0< tanx< 1\)

Tổng trên vẫn là tổng cấp số nhân lùi vô hạn với \(\left\{{}\begin{matrix}u_1=1\\q=-tanx\end{matrix}\right.\)

\(\Rightarrow S=\dfrac{1}{1+tanx}\)

a, \(cos^2x-cosx=0\)

\(\Leftrightarrow cosx\left(cosx-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=0\end{matrix}\right.\)

b, \(2sin2x+\sqrt{2}sin4x=0\)

\(\Leftrightarrow2sin2x+2\sqrt{2}sin2x.cos2x=0\)

\(\Leftrightarrow sin2x\left(1+\sqrt{2}cos2x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\1+\sqrt{2}cos2x=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=k\pi\\cos2x=-\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\2x=\dfrac{3\pi}{4}+k2\pi\\2x=\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\x=\dfrac{3\pi}{8}+k\pi\\x=\dfrac{\pi}{8}+k\pi\end{matrix}\right.\)

a, \(cos^2x-cosx=0\)

\(\Leftrightarrow cosx\left(cosx-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=k2\pi\end{matrix}\right.\) (k ∈ Z)

Vậy...

b, \(2sin2x+\sqrt{2}sin4x=0\)

\(\Leftrightarrow2sin2x+2\sqrt{2}sin2x.cos2x=0\)

\(\Leftrightarrow2sin2x\left(1+\sqrt{2}cos2x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\cos2x=\dfrac{-\sqrt{2}}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}2x=k\pi\\2x=\pm\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\x=\pm\dfrac{3\pi}{8}+k\pi\end{matrix}\right.\)

Vậy...

c, \(8cos^2x+2sinx-7=0\)

\(\Leftrightarrow8\left(1-sin^2x\right)+2sinx-7=0\)

\(\Leftrightarrow8sin^2x-2sinx-1=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx=-\dfrac{1}{4}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\\x=arcsin\left(-\dfrac{1}{4}\right)+k2\pi\\x=\pi-arcsin\left(-\dfrac{1}{4}\right)+k2\pi\end{matrix}\right.\)

Vậy...

d, \(4cos^4x+cos^2x-3=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos^2x=\dfrac{3}{4}\\cos^2x=-1\left(loai\right)\end{matrix}\right.\) 

\(\Leftrightarrow\dfrac{cos2x+1}{2}=\dfrac{3}{4}\)

\(\Leftrightarrow cos2x=\dfrac{1}{2}\)

\(\Leftrightarrow2x=\pm\dfrac{\pi}{3}+k2\pi\)

\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+k\pi\)

Vậy...

e, \(\sqrt{3}tanx-6cotx+\left(2\sqrt{3}-3\right)=0\) (ĐK: \(x\ne\dfrac{k\pi}{2}\))

\(\Leftrightarrow\sqrt{3}tanx-\dfrac{6}{tanx}+\left(2\sqrt{3}-3\right)=0\)

\(\Leftrightarrow\sqrt{3}tan^2x+\left(2\sqrt{3}-3\right)tanx-6=0\)

\(\Leftrightarrow\left[{}\begin{matrix}tanx=\sqrt{3}\\tanx=-2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\left(tm\right)\\x=arctan\left(-2\right)+k\pi\end{matrix}\right.\)

Vậy...

c, \(8cos^2x+2sinx-7=0\)

\(\Leftrightarrow-8sin^2x+2sinx+1=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx=-\dfrac{1}{4}\end{matrix}\right.\)

Với \(sinx=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

Với \(sinx=-\dfrac{1}{4}\Leftrightarrow\left[{}\begin{matrix}x=arcsin\left(-\dfrac{1}{4}\right)+k2\pi\\x=\pi-arcsin\left(-\dfrac{1}{4}\right)+k2\pi\end{matrix}\right.\)

d, \(4cos^4x+cos^2x-3=0\)

\(\Leftrightarrow\left(4cos^2x-3\right)\left(cos^2x+1\right)=0\)

\(\Leftrightarrow4cos^2x-3=0\left(\text{Vì }cos^2x+1>0\right)\)

\(\Leftrightarrow cos^2x=\dfrac{3}{4}\)

\(\Leftrightarrow cosx=\pm\dfrac{\sqrt{3}}{2}\)

Với \(cosx=\dfrac{\sqrt{3}}{2}\Leftrightarrow x=\pm\dfrac{\pi}{3}+k2\pi\)

Với \(cosx=-\dfrac{\sqrt{3}}{2}\Leftrightarrow x=\pm\dfrac{5\pi}{6}+k2\pi\)

\(\Leftrightarrow sin4x=-cos5x\)

\(\Leftrightarrow sin4x=sin\left(5x-\frac{\pi}{2}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}5x-\frac{\pi}{2}=4x+k2\pi\\5x-\frac{\pi}{2}=\pi-4x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k2\pi\\x=\frac{\pi}{6}+\frac{k2\pi}{9}\end{matrix}\right.\)

a, \(\dfrac{1+cosx+cos2x+cos3x}{2cos^2x+cosx-1}\)

\(=\dfrac{1+cos2x+cosx+cos3x}{2cos^2x+cosx-1}\)

\(=\dfrac{2cos^2x+2cos2x.cosx}{cos2x+cosx}\)

\(=\dfrac{2cosx\left(cos2x+cosx\right)}{cos2x+cosx}=2cosx\)

b) \(cos\dfrac{5x}{2}.cos\dfrac{3x}{2}+sin\dfrac{7x}{2}.sin\dfrac{x}{2}\)

\(=cos\dfrac{4x+x}{2}.cos\dfrac{4x-x}{2}+sin\dfrac{4x+3x}{2}.sin\dfrac{4x-3x}{2}\)

\(=\dfrac{1}{2}\left(cos4x+cosx\right)-\dfrac{1}{2}\left(cos4x-cos3x\right)\)

\(=\dfrac{1}{2}\left(cosx+cos3x\right)=\dfrac{1}{2}.2cos2x.cos\left(-x\right)\)\(=cosx.cos2x\)