Viết các biểu thức dưới dạng lập phương của một tổng hoặc hiệu:
a) a 3 + 12 a 2 + 48a + 64;
b) – b 3 + 6 b 2 + 12b + 8;
c) ( m – n ) 6 – 6 ( m – n ) 4 + 12 ( m – n ) 2 – 8;
d) 8 27 a 3 − 8 3 a 2 b + 8 b 2 a − 8 b 3 .
Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc 1 hiệu:
a,-x^3/8+3/4x^2-3/2x+1
b,x^6-3/2x^4y+3/4x^2y^2-1/8y^3
`a,-x^3/8 + 3/(4x^2) - 3/(2x) +1`
`=-(x^3/8 - 3/(4x^2) + 3/(2x) - 1)`
`=-(x/2 - 1)^3`
`b,x^6 - 3/(2x^{4} y) + 3/(4x^{2}y^{2}) - 1/(8y^{3})`
`=(x^3 - 1/(2y))^{3}`
Bài 1. Thực hiện phép tính:
a) (3a+1)3 b) (4-2b)3
c) (2c-3d)3 d) (3x/y-2y/x)3
Bài 2. Viết các biểu thức dưới dạng lập phương của một tổng hoặc hiệu:
a) x3+3x2+3x+1 b) m3+9m2n+27mn2+27n3
c) 8u3-48u2v+96uv2(4v)3
BÀI 3. Rút gọn biểu thức:
a) A=(a+b)3-(a-b)3
b) A=(u-v)3+3uv(u+v)
c) C=6(c-d)(c+d)+2(c-d)2-(c-d)3
Bài 4. Tính nhanh:
a) 1013 b) 2993 c) 993
Bài 5: Tìm x, biết:
a) x3-1-(x2+2x)(x-2)=5
b) (x+1)3-(x-1)3-6(x-1)2=-10
Bài 1. Thực hiện phép tính:
a) (3a+1)3 b) (4-2b)3
c) (2c-3d)3 d) (3x/y-2y/x)3
Bài 2. Viết các biểu thức dưới dạng lập phương của một tổng hoặc hiệu:
a) x3+3x2+3x+1 b) m3+9m2n+27mn2+27n3
c) 8u3-48u2v+96uv2(4v)3
Bài 1. Thực hiện phép tính:
b) (4-2b)3 c) (2c-3d)3
d) (3x/y-2y/x)3
Bài 2. Viết các biểu thức dưới dạng lập phương của một tổng hoặc hiệu:
a) x3+3x2+3x+1 b) m3+9m2n+27mn2+27n3
c) 8u3-48u2v+96uv2(4v)3
Bài 3.Tìm x, biết:
b) (x+1)3-(x-1)3-6(x-1)2=-10
Bài 3:
b: Ta có: \(\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-10\)
\(\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6\left(x^2-2x+1\right)+10=0\)
\(\Leftrightarrow6x^2+12-6x^2+12x-6=0\)
hay \(x=-\dfrac{1}{2}\)
Bài 2:
a: \(x^3+3x^2+3x+1=\left(x+1\right)^3\)
b: \(m^3+9m^2n+27mn^2+27n^3=\left(m+3n\right)^3\)
Viết biểu thức sau dưới dạng lập phương của 1 tổng hoặc hiệu:
a) 4x2 + x4 + 4
b) (-x + 2y)2 + 2(2y - x) + 1
c) (2a - 4b)2 + 4a - 8b + 1
a) \(x^4+4x^2+4=\left(x^2+2\right)^2\)
b) \(\left(2y-x\right)^2+2\left(2y-x\right)+1=\left(2y-x+1\right)^2\)
c) \(\left(2a-4b\right)^2+4a-8b+1=\left(2a-4b\right)^2+2\cdot\left(2a-4b\right)\cdot1+1^2=\left(2a-4b+1\right)^2\)
Bài 1. Khai triển các hằng đẳng thức sau:
a) (2x+1)3 b) (x-3)3
c) (-5x-y)3 h) (3y-2x2)3
Bài 2. Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc lập phương của một hiệu.
a) x3+15x2+75x+125
b) 1-15y+75y2+125y3
c) 8x3+4x2y+3/2 xy2+8y3
d) -8x2+36x2-54+27
a) \(\left(2x+1\right)^3\)
\(=\left(2x\right)^3+3.\left(2x\right)^2.1+3.2x.1+1\)
\(=8x^3+12x^2+6x+1\)
b) \(\left(x-3\right)^3\)
\(=x^3-3.x^2.3+3.x.3^2-3^3\)
\(=x^3-9x^2+27x-27\)
Bài 2:
a: \(x^3+15x^2+75x+125=\left(x+5\right)^3\)
b: \(1-15y+75y^2-125y^3=\left(1-5y\right)^3\)
c: \(8x^3+4x^2y+\dfrac{3}{2}xy^2+8y^3=\left(2x+2y\right)^3\)
Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:
a) \({a^2} + 10ab + 25{b^2}\) b) \(1 + 9{a^2} - 6a\)
`a, a^2 + 10ab + 25b^2 = (a+5b)^2`
`b, 1 + 9a^2 - 6a = (3a-1)^2`
a) \(a^2+10ab+25b^2\)
\(=a^2+2\cdot5b\cdot a+\left(5b\right)^2\)
\(=\left(a+5b\right)^2\)
b) \(1+9a^2-6a\)
\(=1-6a+9a^2\)
\(=\left(1+3a\right)^2\)
a) a2 + 10ab + 25b2
= a2 + 2.a.5b + (5b)2
= (a + 5b)2
b) 1 + 9a2 - 6a
= 9a2 - 6a + 1
= (3a)2 - 2.3a.1 + 12
= (3a - 1)2
Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu
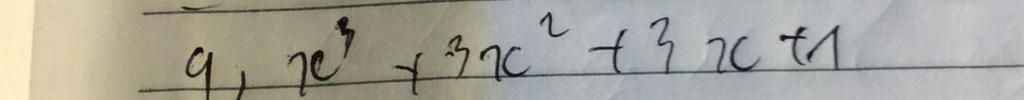
HĐT số 4: \(\left(A+B\right)^3=A^3+3A^2B+3AB^2+B^3\)
__________
\(x^3+3x^2+3x+1\)
\(=x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3\)
\(=\left(x+1\right)^3\)
`x^3 +3x^2+3x+1`
`= x^3 + 3*x^2*1 +3*x*1^2 +1^3`
`=(x+1)^3`
x^3 + 3x^2 + 3x + 1
<=> x^3 + 3x^2.1 + 3x.1^2 + 1^3
<=> (x + 1) ^3
Bài 1. Khai triển các hằng đẳng thức sau:
c) (-5x-y)3 h) (3y-2x2)3
Bài 2. Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc lập phương của một hiệu.
d) -8x2+36x2-54+27
Bài 1:
c: \(\left(-5x-y\right)^3=-125x^3-75x^2y-15xy^2-y^3\)
h: \(\left(3y-2x^2\right)^3=27y^3-54y^2x^2+36yx^4-8x^6\)
Bài 1:
c. (-5x - y)3 = -125x3 - 50x2y - 10xy2 - y3
d. (3y - 2x2)3 = 27y3 - 18x2y2 + 24xy4 - 8x6