Cho E:\(\left(-3;\frac{1}{a}\right)\) , F:(a;\(+\infty\) )
tìm a để E\(\cap\) F \(\ne\phi\)
Cho \(E=\left\{x\in Z|\left|x\right|\le5\right\}\); \(A=\left\{x\in R|x^2+3x-4=0\right\}\);
\(B=\left\{x\in Z|(x-2)(x+1)(2x^2-x-3)=0\right\}\)
a) CM \(A\subset E\),\(B\subset E\)
b) Tìm \(E\backslash\left(A\cap B\right)\),\(E\backslash\left(A\cup B\right)\) rồi tìm quan hệ giữa hai tập hợp này.
\(E=\left\{-5;-4;-3;-2;-1;0;1;2;3;4;5\right\}\)
\(A=\left\{1;-4\right\}\)
\(B=\left\{2;-1\right\}\)
a) Với mọi x thuộc A đều thuộc E \(\Rightarrow A\subset E\)
Với mọi x thuộc B đều thuộc E \(\Rightarrow B\subset E\)
b) \(A\cap B=\varnothing\)
\(\Rightarrow E\backslash\left(A\cap B\right)=\left\{-5;-4;-3;-2;-1;0;1;2;3;4;5\right\}\)
\(A\cup B=\left\{-4;-1;1;2\right\}\)
\(\Rightarrow E\backslash\left(A\cup B\right)=\left\{-5;-3;-2;0;3;4;5\right\}\)
\(\Rightarrow E\backslash\left(A\cup B\right)\subset E\backslash\left(A\cap B\right)\)
Cho a,b>0 thỏa mãn a+b=1.Tìm GTNN của A=\(\left(a^3+\dfrac{1}{b^3}\right)\left(b^3+\dfrac{1}{a^3}\right)\)
MN giúp e với e cần gấp ạ
\(A=a^3b^3+\dfrac{1}{a^3b^3}+2=a^3b^3+\dfrac{1}{2^{12}.a^3b^3}+\dfrac{2^{12}-1}{2^{12}a^3b^3}+2\)
\(A\ge2\sqrt{\dfrac{a^3b^3}{2^{12}.a^3b^3}}+\dfrac{2^{12}-1}{2^{12}.\left(\dfrac{a+b}{2}\right)^6}+2=\dfrac{2}{2^6}+\dfrac{2^{12}-1}{2^6}+2=\dfrac{2^{12}+1}{2^6}+2\) (casio)
Dấu "=" xảy ra khi \(a=b=\dfrac{1}{2}\)
CHO E=\(\left(\frac{x^3}{x^3-4x}+\frac{6}{6-3x}+\frac{1}{2+x}\right):\left(x+2+\frac{10-x^2}{x-2}\right)\)
a) Rut gon E
b) Tim x thuoc Z sao cho E thuoc Z
\(E=\frac{x.\left(1-x\right)^2}{1+x^2}:\left(\left(\frac{1-x^3}{1-x}+x\right)\left(\frac{1+x^3}{1+x}-x\right)\right)\)
a.rút gọn E
b.chứng minh E>0 với mọi giá trị x>0
ai làm đc mình sẽ cho 1 like
1, Cho x+y=1. Tính B=\(4.\left(x^3+y^3\right)-6\left(x^2+y^2\right)\)
Giúp e vs ạ!
Đây nè bạn. Mk chỉ mới nghĩ ra cách này thôi à!!! Bạn nào có cách nào thì bảo mk với nhé!!!
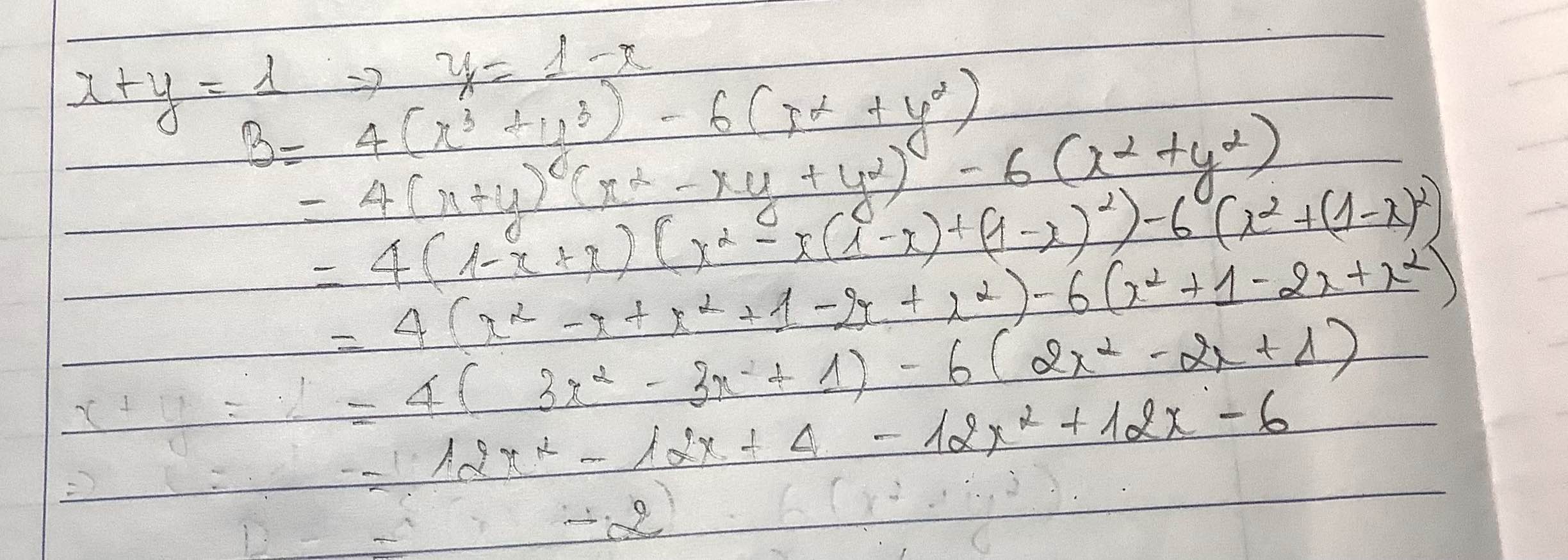
\(B=4\left(x+y\right)\left(x^2+y^2-xy\right)-6\left[\left(x+y\right)^2-2xy\right]\)
\(=4\left[\left(x+y\right)^2-3xy\right]-6\left(1-2xy\right)\)
\(=4-12xy-6+12xy\)
\(=-2\)
Cho E =\(\left(1-\dfrac{1}{1+2}\right)\left(1-\dfrac{1}{1+2+3}\right)...\left(1-\dfrac{1}{1+2+3+...+n}\right)\)
Cho
\(\frac{A+C+E}{3}=40--\left(1\right)\)
\(\frac{A+B+D}{3}=28--\left(2\right)\)
\(\frac{B+C+D+E}{3}=33--\left(3\right)\)
\(A=?\)
Trong mặt phẳng Oxy, cho ba điểm \(D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)\)
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy
b) Tìm tọa độ của các vectơ \(\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF} \).
c) Vẽ và tìm tọa độ hai vectơ đơn vị và \(\overrightarrow j \)lần lượt trên hai trục tọa độ Ox và Oy
a)
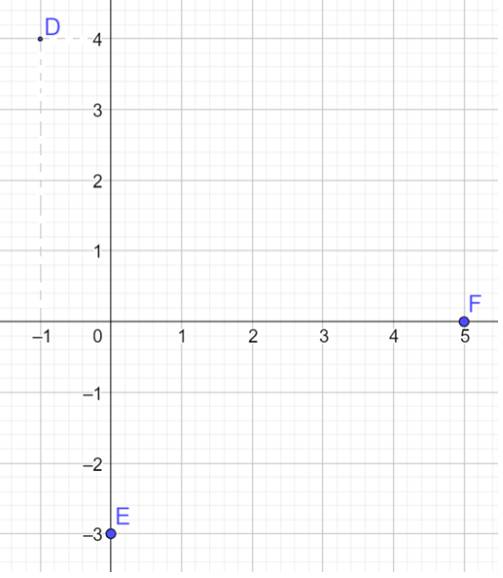
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
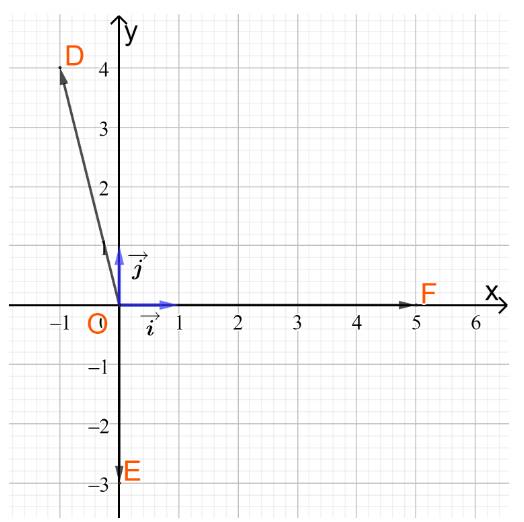
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)
Cho \(\left(x+\sqrt{x^2+3}\right)\left(y+\sqrt{y^2+3}\right)=3\)
Tính E = x + y
Ta có: \(\left(x+\sqrt{x^2+3}\right)\left(\sqrt{x^2+3}-x\right)=3\)
\(\left(y+\sqrt{y^2+3}\right)\left(\sqrt{y^2+3}-y\right)=3\)
Kết hợp với giả thiết ta có:
\(\sqrt{x^2+3}-x=y+\sqrt{y^2+3}\)
\(\sqrt{y^2+3}-y=x+\sqrt{x^2+3}\)
Cộng theo vế ta được: \(-\left(x+y\right)=x+y\)
\(\Rightarrow\)\(E=x+y=0\)
\(\left(x+\sqrt{x^2+3}\right)\left(y+\sqrt{y^2+3}\right)=3\)
\(\Leftrightarrow\left(x+\sqrt{x^2+3}\right)\left(x-\sqrt{x^2+3}\right)\left(y+\sqrt{y^2+3}\right)=3\left(x-\sqrt{x^2+3}\right)\)
\(\Leftrightarrow\left(x^2-x^2-3\right)\left(y+\sqrt{y^2+3}\right)=3\left(x-\sqrt{x^2+3}\right)\)
\(\Leftrightarrow-3\left(y+\sqrt{y^2+3}\right)=3\left(x-\sqrt{x^2+3}\right)\)
\(\Leftrightarrow-y-\sqrt{y^2+3}=x-\sqrt{x^2+3}\)(*)
Tương tự, nhân mỗi vế vs \(y-\sqrt{y^2+3}\), ta được:
\(-x-\sqrt{x^2+3}=y-\sqrt{y^2+3}\)(**)
Cộng (*) và (**) suy ra :
\(-y-x-\sqrt{y^2+3}-\sqrt{x^2+3}=x+y-\sqrt{x^2+3}-\sqrt{y^2+3}\)
\(\Leftrightarrow-y-x=x+y\Leftrightarrow2\left(x+y\right)=0\Leftrightarrow x+y=0\)
Vậy \(E=0.\)
1. Cho tập hợp \(E=\left\{a,b,c,d\right\}\); \(\left\{F=b,c,e,g\right\}\); \(G=\left\{c,d,e,f\right\}\)
CMR: \(E\cap\left(F\cup G\right)=\left(E\cap F\right)\cup\left(E\cap G\right)\)
Mọi người giúp em với ạ. E cảm ơn