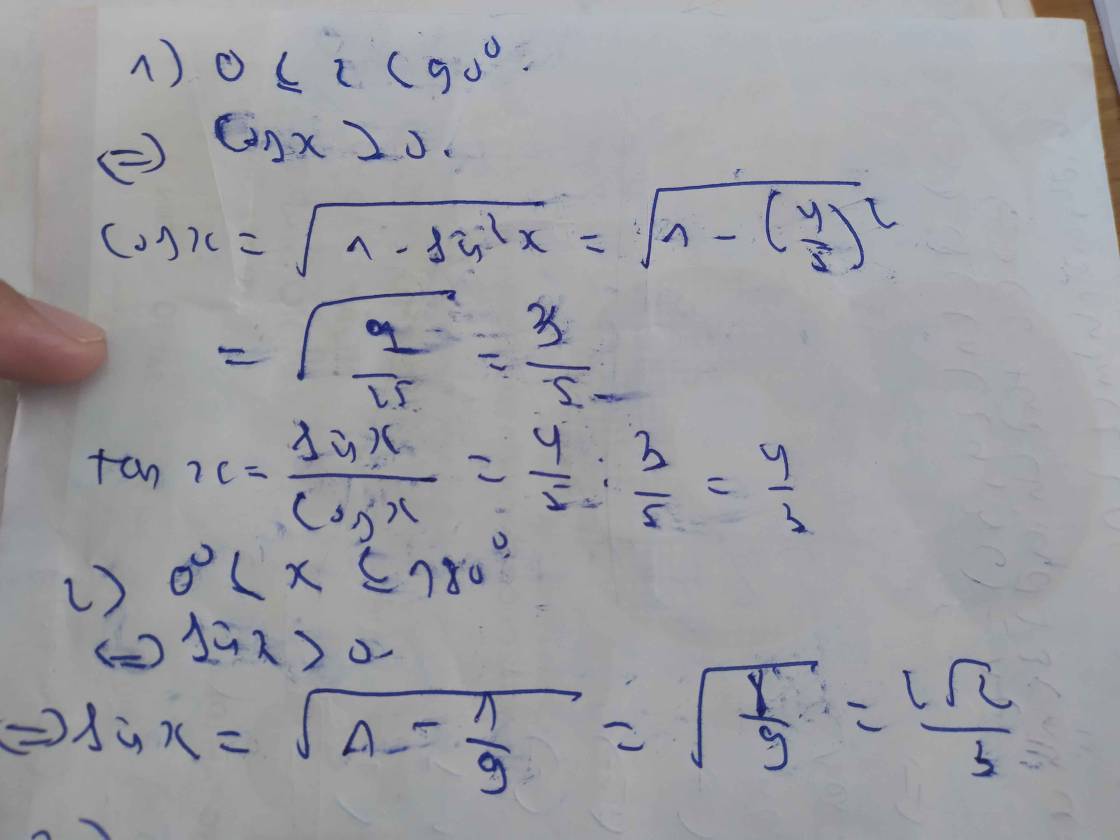Cho 0\(\le\) x \(\le\) \(\dfrac{1}{2}\). Tìm GTLN của f(x)= 3x(1-2x)

Những câu hỏi liên quan
Tìm GTLN của biểu thức :
\(Q=4x^2-3x^3\) với \(0\le x\le\dfrac{4}{3}\)
\(Q=x^2\left(4-3x\right)=\dfrac{4}{9}.\dfrac{3}{2}x.\dfrac{3}{2}x\left(4-3x\right)\)
\(Q\le\dfrac{1}{27}.\dfrac{4}{9}.\left(\dfrac{3x}{2}+\dfrac{3x}{2}+4-3x\right)^3=\dfrac{256}{243}\)
\(Q_{maxx}=\dfrac{256}{243}\) khi \(\dfrac{3x}{2}=4-3x\Leftrightarrow x=\dfrac{8}{9}\)
Đúng 2
Bình luận (0)
TÌM GTNN CỦA HÀM SỐ SAU:
a) y=\(\dfrac{x^2+x+2}{\sqrt{x^2+x+1}}\)
TÌM GTLN CỦA HÀM SỐ SAU:
b)y= \(x^2\sqrt{9-x^2}với-3\le x\le3\)
c)y=\(\left(1-x\right)^3\left(1+3x\right)với\dfrac{-1}{3}\le x\le1\)
\(a,\dfrac{x^2+x+2}{\sqrt{x^2+x+1}}=\dfrac{x^2+x+1+1}{\sqrt{x^2+x+1}}=\sqrt{x^2+x+1}+\dfrac{1}{\sqrt{x^2+x+1}}\left(1\right)\)
Áp dụng BĐT cosi: \(\left(1\right)\ge2\sqrt{\sqrt{x^2+x+1}\cdot\dfrac{1}{\sqrt{x^2+x+1}}}=2\)
Dấu \("="\Leftrightarrow x^2+x+1=1\Leftrightarrow x^2+x=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Đúng 3
Bình luận (0)
\(A=\left(\dfrac{x-1}{x^2-2x}+\dfrac{x+1}{x^2+2x}-\dfrac{4}{x^3-4x}\right)\div\dfrac{2x+4}{x^2-3x}\)
Tìm giátrị x để A \(\le\)0
\(A=\dfrac{x^2+x-2+x^2-x-2-4}{x\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x-3\right)}{2\left(x+2\right)}=\dfrac{2\left(x-2\right)\left(x+2\right)\left(x-3\right)}{2\left(x-2\right)\left(x+2\right)^2}=\dfrac{x-3}{x+2}\\ A\le0\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-3\ge0\\x+2< 0\end{matrix}\right.\\\left\{{}\begin{matrix}x-3\le0\\x+2>0\end{matrix}\right.\end{matrix}\right.\Rightarrow-2< x< 3;x\ne0\left(ĐKXD\right)\)
Đúng 1
Bình luận (0)
Tìm GTLN\(B=3x\left(1-2x\right),0\le x\le\frac{1}{2}\)
\(B=\frac{3}{2}.2x\left(1-2x\right)\le\frac{3}{2}\frac{\left(2x+1-2x\right)^2}{4}=\frac{3}{8}\)
\(\Rightarrow B_{max}=\frac{3}{8}\) khi \(2x=1-2x\Rightarrow x=\frac{1}{4}\)
Đúng 0
Bình luận (0)
cho \(3x^2+2y^2\le\dfrac{6}{35}\). tìm GTLN của \(S=2x+3y\)
Lời giải:
Áp dụng BĐT Bunhiacopxky:
\(S^2=(2x+3y)^2\leq (3x^2+2y^2)\left(\frac{4}{3}+\frac{9}{2}\right)\leq \frac{6}{35}(\frac{4}{3}+\frac{9}{2})=1\)
\(\Rightarrow S\leq 1\)
Vậy $S_{\max}=1$. Giá trị này đạt tại \(\left\{\begin{matrix} 3x^2+2y^2=\frac{6}{35}\\ \frac{3}{2}x=\frac{2}{3}y\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{4}{35}\\ y=\frac{9}{35}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Lời giải:
Áp dụng BĐT Bunhiacopxky:
\(S^2=(2x+3y)^2\leq (3x^2+2y^2)\left(\frac{4}{3}+\frac{9}{2}\right)\leq \frac{6}{35}(\frac{4}{3}+\frac{9}{2})=1\)
\(\Rightarrow S\leq 1\)
Vậy $S_{\max}=1$. Giá trị này đạt tại \(\left\{\begin{matrix} 3x^2+2y^2=\frac{6}{35}\\ \frac{3}{2}x=\frac{2}{3}y\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{4}{35}\\ y=\frac{9}{35}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
1) cho góc x (0 độ le x 90 độ) thỏa mãn sinxdfrac{4}{5} giá trị của tanx là 2) cho góc x (0 độ le x le 180 độ) thỏa mãn cosxdfrac{1}{3} giá trị của sinx là3) cho cosxdfrac{1}{2} tính P3sin^2x+4cos^2x
Đọc tiếp
1) cho góc x (0 độ \(\le\) x < 90 độ) thỏa mãn \(sinx=\dfrac{4}{5}\) giá trị của \(tanx\) là
2) cho góc x (0 độ \(\le\) x \(\le\) 180 độ) thỏa mãn \(cosx=\dfrac{1}{3}\) giá trị của \(sinx\) là
3) cho \(cosx=\dfrac{1}{2}\) tính \(P=3sin^2x+4cos^2x\)
Giải hệ bpt
1) \(-4\le\dfrac{x^2-2x-7}{x^2+1}\le1\)
2) \(\dfrac{1}{13}\le\dfrac{x^2-2x-2}{x^2-5x+7}\le1\)
3) \(-1< \dfrac{10x^2-3x-2}{-x^2+3x-2}< 1\)
1.
\(-4\le\dfrac{x^2-2x-7}{x^2+1}\le1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-2x-7\le x^2+1\\-4x^2-4\le x^2-2x-7\end{matrix}\right.\) (Do \(x^2+1>0\))
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-4\\\left[{}\begin{matrix}x\ge1\\x\le-\dfrac{3}{5}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge1\\-4\le x\le-\dfrac{3}{5}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
2.
\(\dfrac{1}{13}\le\dfrac{x^2-2x-2}{x^2-5x+7}\le1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-5x+7\le13x^2-26x-26\\x^2-2x-2\le x^2-5x+7\end{matrix}\right.\) (Do \(x^2-5x+7>0\))
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge\dfrac{11}{4}\\x\le-1\end{matrix}\right.\\x\le3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{11}{4}\le x\le3\\x\le-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm GTNN của biểu thức sau:
\(N=\dfrac{3x}{2}+\dfrac{1}{x+1}\) với \(x>-1\)
Tìm GTLN của biểu thức:
\(Q=\left(6x+3\right)\left(5-2x\right)\) với\(\dfrac{-1}{2}\le x\le\dfrac{5}{2}\)
a,Cho x,y,z tm \(\left\{{}\begin{matrix}x^2+y^2+z^2=8\\x+y+z=4\end{matrix}\right.\). CM: \(-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)
b, cho \(x^2+3y^2=1\). Tìm GTLN, GTNN của\(P=x-y\)
c, Cho \(P=\dfrac{x^2-\left(x-4y\right)^2}{x^2+4y^2}\left(x^2+y^2>0\right)\)
Tìm GTLN của P
\(c,P=\dfrac{x^2-x^2+8xy-16y^2}{x^2+4y^2}=\dfrac{8\left(\dfrac{x}{y}\right)-16}{\left(\dfrac{x}{y}\right)^2+4}\)
Đặt \(\dfrac{x}{y}=t\)
\(\Leftrightarrow P=\dfrac{8t-16}{t^2+4}\Leftrightarrow Pt^2+4P=8t-16\\ \Leftrightarrow Pt^2-8t+4P+16=0\)
Với \(P=0\Leftrightarrow t=2\)
Với \(P\ne0\Leftrightarrow\Delta'=16-P\left(4P+16\right)\ge0\)
\(\Leftrightarrow-P^2-4P+4\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Vậy \(P_{max}=-2+2\sqrt{2}\Leftrightarrow t=\dfrac{4}{P}=\dfrac{4}{-2+2\sqrt{2}}=2+\sqrt{2}\)
\(\Leftrightarrow\dfrac{x}{y}=2+2\sqrt{2}\)
Đúng 3
Bình luận (2)
Bài a hình như sai đề rồi bạn.
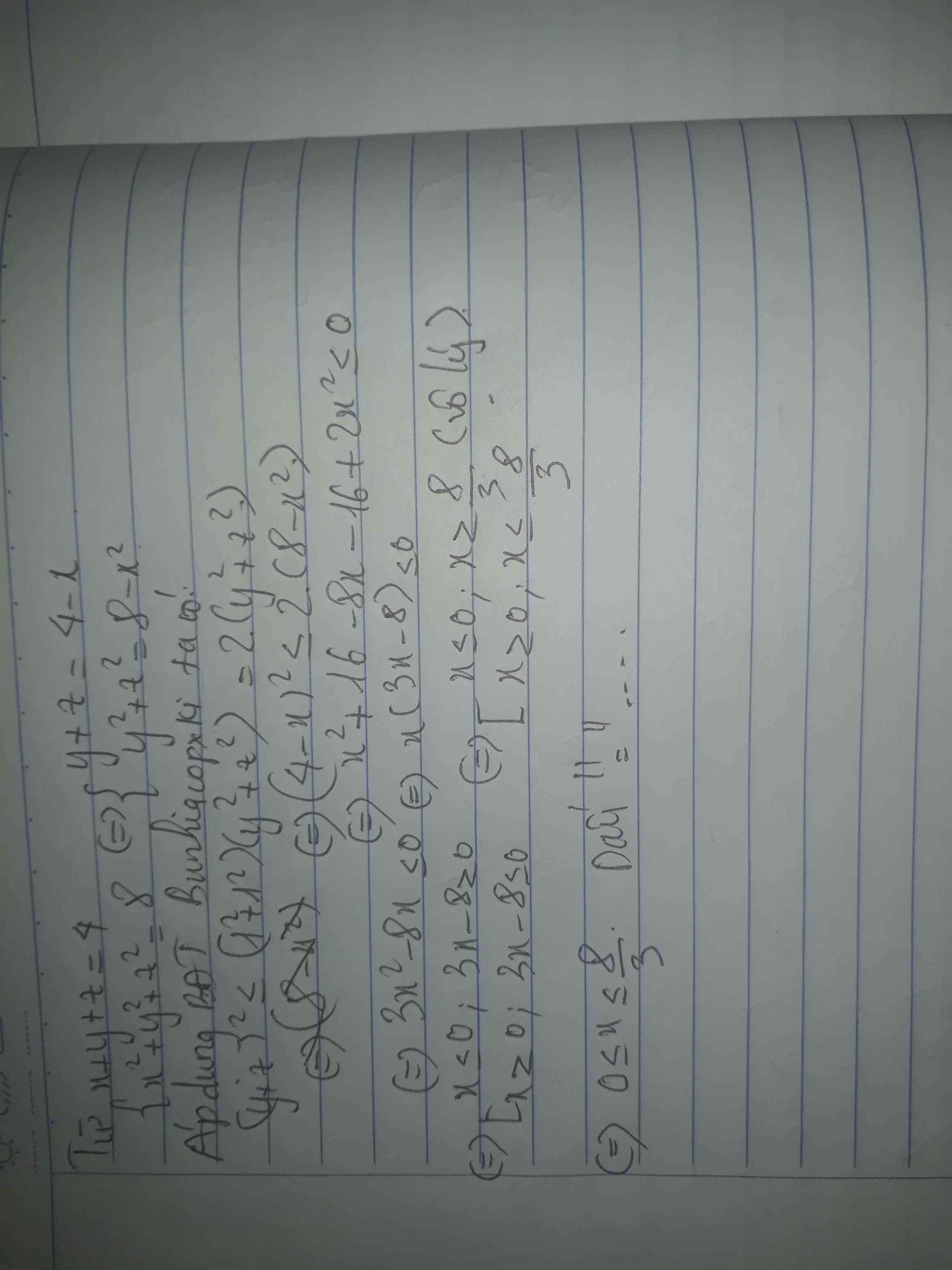
Đúng 3
Bình luận (2)
\(a,\text{Đặt }\left\{{}\begin{matrix}S=y+z\\P=yz\end{matrix}\right.\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\left(y+z\right)^2-2yz+x^2=8\\x\left(y+z\right)+yz=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S^2-2P+x^2=8\\Sx+P=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2-2\left(4-Sx\right)+x^2=8\\P=4-Sx\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2+2Sx+x^2-16=0\left(1\right)\\P=4-Sx\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\left(S+x-4\right)\left(S+x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}S=-x+4\Rightarrow P=\left(x-2\right)^2\\S=-x-4\Rightarrow P=\left(x+2\right)^2\end{matrix}\right.\)
Mà y,z là nghiệm của hệ nên \(S^2-4P\ge0\Leftrightarrow\left[{}\begin{matrix}\left(4-x\right)^2\ge4\left(x-2\right)^2\\\left(-4-x\right)^2\ge4\left(x+2\right)^2\end{matrix}\right.\Leftrightarrow-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời