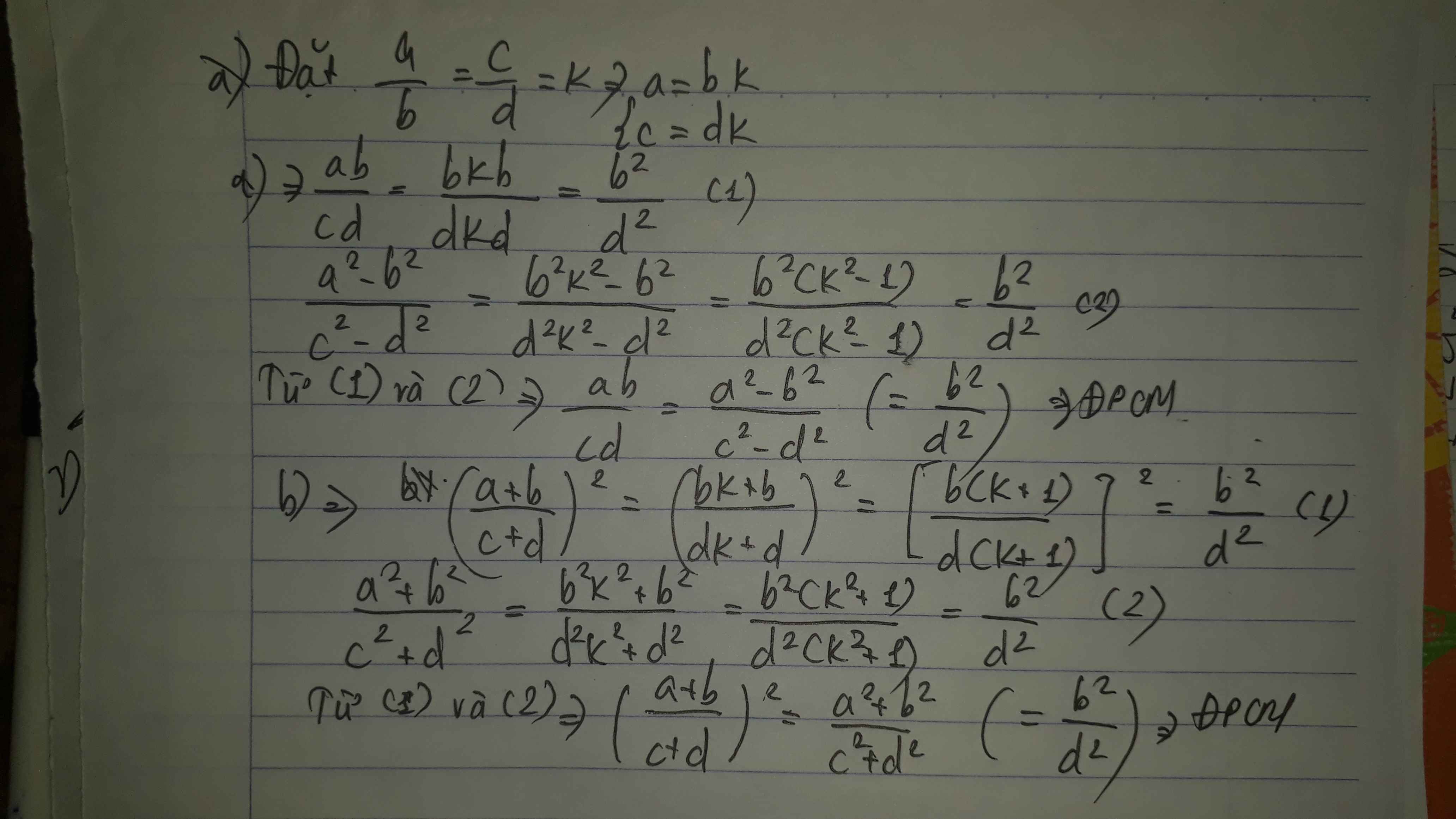Cho tỉ lệ thức \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\).CMR:\(\dfrac{a+b}{a-b}\)=\(\dfrac{c+d}{c-d}\)

Những câu hỏi liên quan
1) Cho tỉ lệ thức dfrac{a}{b}dfrac{c}{d}. CMR(với giả thiết các tỉ số đều có nghĩa)
a)dfrac{a-b}{a+b}dfrac{c-d}{c+d}
b)dfrac{ab}{cd}dfrac{left(a-bright)^2}{left(c-dright)^2}
c)dfrac{2a+5b}{3a-4b}dfrac{2c+5d}{3c-4d}
2) Cho tỉ lệ thức dfrac{a}{b}dfrac{c}{d}. CMR ta có các tỉ lệ thức sau
a)dfrac{a}{a+b}dfrac{c}{c+d}
b)dfrac{7a1^2+5ac}{7a^2-5ac}dfrac{7b^2+5bd}{7b^2-5bd}
3) CMR nếu a^2bc thì dfrac{a+b}{a-b}dfrac{c+a}{c-a}. Đảo lại có đúng không?
4) CMR nếu dfrac{a}{b}dfrac{b}{d} thì dfrac{a^...
Đọc tiếp
1) Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\). CMR(với giả thiết các tỉ số đều có nghĩa)
a)\(\dfrac{a-b}{a+b}=\dfrac{c-d}{c+d}\)
b)\(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
c)\(\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
2) Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\). CMR ta có các tỉ lệ thức sau
a)\(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
b)\(\dfrac{7a1^2+5ac}{7a^2-5ac}=\dfrac{7b^2+5bd}{7b^2-5bd}\)
3) CMR nếu \(a^2=bc\) thì \(\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\). Đảo lại có đúng không?
4) CMR nếu \(\dfrac{a}{b}=\dfrac{b}{d}\) thì \(\dfrac{a^2+b^2}{b^2+d^2}=\dfrac{a}{d}\)
5) Cho tỉ lệ thức \(\dfrac{a^2+b^2}{c^2+d^2}=\dfrac{ab}{cd}.CMR\dfrac{a}{b}=\dfrac{c}{d}\)
các bn giúp bn Heo Mách với nha
Bài 2:
Đặt a/b=c/d=k
=>a=bk; c=dk
a: \(\dfrac{a}{a+b}=\dfrac{bk}{bk+b}=\dfrac{k}{k+1}\)
\(\dfrac{c}{c+d}=\dfrac{dk}{dk+d}=\dfrac{k}{k+1}\)
Do đó: \(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
b: \(\dfrac{7a^2+5ac}{7a^2-5ac}=\dfrac{7\cdot b^2k^2+5\cdot bk\cdot dk}{7\cdot b^2k^2-5\cdot bk\cdot dk}\)
\(=\dfrac{7b^2k^2+5bdk^2}{7b^2k^2-5bdk^2}=\dfrac{7b^2+5bd}{7b^2-5bd}\)(đpcm)
Đúng 0
Bình luận (0)
Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\).CMR (a+2c)(b+d) = (a+c)(b+2d)
Đặt a/b=c/d=k
=>a=bk; c=dk
\(\left(a+2c\right)\left(b+d\right)=\left(bk+2dk\right)\left(b+d\right)=k\left(b+2d\right)\left(b+d\right)\)
\(\left(a+c\right)\left(b+2d\right)=\left(bk+dk\right)\left(b+2d\right)=k\left(b+d\right)\left(b+2d\right)\)
Do đó: VT=VP
Đúng 0
Bình luận (0)
1. Cho tỉ lệ thức dfrac{a}{b} dfrac{c}{d}. CMR:
a) dfrac{3a+5c}{3b+5d} dfrac{a-2c}{b-2d}.
b) dfrac{a^2-b^2}{ab} dfrac{c^2-d^2}{cd}.
c) dfrac{left(a+bright)^2}{a^2+b^2} dfrac{left(c+dright)^2}{c^2+d^2}.
d) left(dfrac{a+b}{c+d}right)^3 dfrac{a^3+b^3}{c^3+d^3}.
Gíup mình với cảm ơn các bạn rất nhiều!!!!!!!!!
Đọc tiếp
1. Cho tỉ lệ thức \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\). CMR:
a) \(\dfrac{3a+5c}{3b+5d}\) = \(\dfrac{a-2c}{b-2d}\).
b) \(\dfrac{a^2-b^2}{ab}\) = \(\dfrac{c^2-d^2}{cd}\).
c) \(\dfrac{\left(a+b\right)^2}{a^2+b^2}\) = \(\dfrac{\left(c+d\right)^2}{c^2+d^2}\).
d) \(\left(\dfrac{a+b}{c+d}\right)^3\) = \(\dfrac{a^3+b^3}{c^3+d^3}\).
Gíup mình với cảm ơn các bạn rất nhiều!!!!!!!!!
Ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
a) \(\dfrac{3a+5c}{3b+5d}=\dfrac{3\cdot bk+5\cdot dk}{3b+5d}=\dfrac{k\left(3b+5d\right)}{3b+5d}=k\) (1)
\(\dfrac{a-2c}{b-2d}=\dfrac{bk-2dk}{b-2d}=\dfrac{k\left(b-2d\right)}{b-2d}=k\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{3a+5c}{3b+5d}=\dfrac{a-2c}{b-2d}\left(dpcm\right)\)
b) \(\dfrac{a^2-b^2}{ab}=\dfrac{\left(bk\right)^2-b^2}{bk\cdot b}=\dfrac{b^2k^2-b^2}{b^2k}=\dfrac{b^2\left(k-1\right)}{b^2k}=\dfrac{k-1}{k}\)(1)
\(\dfrac{c^2-d^2}{cd}=\dfrac{\left(dk\right)^2-d^2}{dk\cdot d}=\dfrac{d^2k^2-d^2}{d^2k}=\dfrac{d^2\left(k-1\right)}{d^2k}=\dfrac{k-1}{k}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{a^2-b^2}{ab}=\dfrac{c^2-d^2}{cd}\left(dpcm\right)\)
c) \(\left(\dfrac{a+b}{c+d}\right)^3=\left(\dfrac{bk+b}{dk+d}\right)^3=\dfrac{b^3\left(k+1\right)^3}{d^3\left(k+1\right)^3}=\dfrac{b^3}{d^3}\) (1)
\(\dfrac{a^3+b^3}{c^3+d^3}=\dfrac{\left(bk\right)^3+b^3}{\left(dk\right)^3+d^3}=\dfrac{b^3k^3+b^3}{d^3k^3+d^3}=\dfrac{b^3\left(k^3+1\right)}{d^3\left(k^3+1\right)}=\dfrac{b^3}{d^3}\) (2)
Từ (1) và (2) \(\Rightarrow\left(\dfrac{a+b}{c+d}\right)^3=\dfrac{a^3+b^3}{c^3+d^3}\left(dpcm\right)\)
Đúng 3
Bình luận (0)
giúp mình câu d) luôn nha phong
cảm ơn phong nha
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\)
CMR:\(\dfrac{a-b}{a+b}=\dfrac{c-d}{c+d}\)
Cách 1 :
Từ a/b = c/d => a/c = b/d ( tính chất tỉ lệ thức )
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
a/c = b/d = a+b/a-b = a-b/c-d => a+b/a-b = c+d/c-d ( tính chất tỉ lệ thức )
Vậy a+b/a-b = c+d/c-d
Cách 2:
Đặt : a/b = c/d = k
a/b = k => a= bk
c/d = k => c=dk
a+b/a-b = bk+b/ bk-b = b(k+1)/b(k-1) = k+1/k-1. (1)
c+d/c-d = dk+d/dk-d = d(k+1)/d(k-1) + k+1/k-1. (2)
Từ (1) và (2) suy ra a+b/a-b = c+d/c-d.
Đúng 0
Bình luận (0)
Ta có:\(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
\(\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
\(=\dfrac{c+d}{a+b}=\dfrac{c-d}{a-b}\)
\(\Rightarrow\dfrac{a-b}{a+b}=\dfrac{c-d}{c+d}\left(dpcm\right)\)
Đúng 0
Bình luận (0)
Chứng minh từ tỉ lệ thức \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\) thì ta suy ra được các tỉ lệ thức sau:\(\dfrac{a+b}{b}\)=\(\dfrac{c+d}{d}\);\(\dfrac{a-b}{b}\)=\(\dfrac{c-d}{d}\) và\(\dfrac{a}{a+b}\)=\(\dfrac{c}{c+d}\).
\(\dfrac{a}{b}=\dfrac{c}{d}=>\dfrac{a}{b}+1=\dfrac{c}{d}+1=>\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
\(\dfrac{a}{b}=\dfrac{c}{d}=>\dfrac{a}{b}-1=\dfrac{c}{d}-1=>\dfrac{a-b}{b}=\dfrac{c-d}{d}\)
\(\dfrac{a}{b}=\dfrac{c}{d}=>ad=cb=>ad+ac=cb+ac\)
\(=>a\left(c+d\right)=c\left(a+b\right)=>\dfrac{a}{c}=\dfrac{a+b}{c+d}=>\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
Đúng 0
Bình luận (0)
a) \(\dfrac{a}{b}=\dfrac{c}{d}\)
nên \(\dfrac{a}{b}+1=\dfrac{c}{d}+1\)
hay \(\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
b) \(\dfrac{a}{b}=\dfrac{c}{d}\)
nên \(\dfrac{a}{b}-1=\dfrac{c}{d}-1\)
hay \(\dfrac{a-b}{b}=\dfrac{c-d}{d}\)
Đúng 0
Bình luận (0)
Chứng minh rằng từ tỉ lệ thức \(\dfrac{a}{b} = \dfrac{c}{d}\) ta suy ra được các tỉ lệ thức sau:
a) \(\dfrac{{a + b}}{b} = \dfrac{{c + d}}{d}\)
b) \(\dfrac{{a - b}}{b} = \dfrac{{c - d}}{d}\)
c) \(\dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\) (các mẫu số phải khác 0)
a) Vì \(\dfrac{a}{b} = \dfrac{c}{d}\) nên \(ad = bc\)
Ta có \(\dfrac{{a + b}}{b} = \dfrac{{c + d}}{d}\)\( \Rightarrow d(a + b) = b(c + d)\)\( \Rightarrow ad + bd = bc + bd\)
\( \Rightarrow ad = bc\) (luôn đúng)
\( \Rightarrow \dfrac{{a + b}}{b} = \dfrac{{c + d}}{d}\)
b) Vì \(\dfrac{a}{b} = \dfrac{c}{d}\) nên \(ad = bc\)
Ta có: \(\dfrac{{a - b}}{b} = \dfrac{{c - d}}{d}\)
\(\begin{array}{l} \Rightarrow d(a - b) = b(c - d)\\ \Leftrightarrow ad - bd = bc - bd\\ \Leftrightarrow ad = bc\end{array}\) ( luôn đúng)
Vậy \(\dfrac{{a - b}}{b} = \dfrac{{c - d}}{d}\)
c) Vì \(\dfrac{a}{b} = \dfrac{c}{d}\) nên \(ad = bc\)
Ta có: \(\dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)
\(\begin{array}{l} \Rightarrow a(c + d) = c(a + b)\\ \Leftrightarrow ac + ad = ac + bc\\ \Leftrightarrow ad = bc\end{array}\) (luôn đúng)
Vậy \(\dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)
Đúng 0
Bình luận (0)
Từ tỉ lệ thức a/bc/d (a,b,c,d khác 0;a khác pm b;cnepm d) hãy suy ra các tỉ lệ thức sau:a,dfrac{a+b}{b} dfrac{c+d}{d}b,dfrac{a-b}{b} dfrac{c-d}{d}c,dfrac{a+b}{a} dfrac{c+d}{c}d,dfrac{a-b}{a} dfrac{c-d}{c}e,dfrac{a}{a+b}dfrac{c}{c+d}f,dfrac{a}{a-b}dfrac{c}{c-d}
Đọc tiếp
Từ tỉ lệ thức a/b=c/d (a,b,c,d khác 0;a khác \(\pm b\);c\(\ne\)\(\pm d\)) hãy suy ra các tỉ lệ thức sau:
a,\(\dfrac{a+b}{b}\) = \(\dfrac{c+d}{d}\)
b,\(\dfrac{a-b}{b}\) = \(\dfrac{c-d}{d}\)
c,\(\dfrac{a+b}{a}\) = \(\dfrac{c+d}{c}\)
d,\(\dfrac{a-b}{a}\) =\(\dfrac{c-d}{c}\)
e,\(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
f,\(\dfrac{a}{a-b}=\dfrac{c}{c-d}\)
a) \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
\(\Rightarrow\dfrac{a+b}{b}=\dfrac{bk+b}{b}=\dfrac{b\left(k+1\right)}{b}=k+1\) và \(\dfrac{c+d}{d}=\dfrac{dk+d}{d}=\dfrac{d\left(k+1\right)}{d}=k+1\)
\(\Rightarrow\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
Đúng 1
Bình luận (0)
b) \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a-b}{b}=\dfrac{b\left(k-1\right)}{b}=k-1\\\dfrac{c-d}{d}=\dfrac{d\left(k-1\right)}{d}=k-1\end{matrix}\right.\)\(\Rightarrow\dfrac{a-b}{b}=\dfrac{c-d}{d}\)
c) \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\Rightarrow\dfrac{a}{c}=\dfrac{a+b}{c+d}\Rightarrow\dfrac{a+b}{a}=\dfrac{c+d}{c}\)
d) \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a}{c}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a-b}{a}=\dfrac{c-d}{c}\)
Đúng 1
Bình luận (0)
e: Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\)
nên \(\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\)
hay \(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
Đúng 1
Bình luận (0)
Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}.CMR:\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\),=> a=bk:c=dk
Ta có : \(\dfrac{ab}{cd}=\dfrac{bkb}{dkd}=\dfrac{kb^2}{kd^2}=\dfrac{b^2}{d^2}\) (1)
\(\dfrac{a^2-b^2}{c^2-d^2}=\dfrac{b^2k^2-b^2}{d^2k^2-d^2}=\dfrac{b^2\left(k^2-1\right)}{d^2\left(k^2-1\right)}=\dfrac{b^2}{d^2}\) (2)
Từ (1) và (2) => \(\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\) (đpcm)
Đúng 0
Bình luận (0)
Từ \(\dfrac{a}{b}=\dfrac{c}{d}\)
=> \(\dfrac{a}{c}=\dfrac{b}{d}\)
=> Ta sẽ có : \(\dfrac{a}{c}\). \(\dfrac{b}{d}\) = \(\dfrac{ab}{cd}\) = \(\dfrac{a^2}{c^2}\) = \(\dfrac{b^2}{d^2}\) (*1)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{a^2}{c^2}=\dfrac{b^2}{d^2}=\dfrac{a^2-b^2}{c^2-d^2}\) (*2)
Từ (1);(2) => \(\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\) (ĐPCM)
Đúng 0
Bình luận (0)
Bài 7: Cho tỉ lệ thức dfrac{a}{b}dfrac{c}{d}. Chứng minh rằng ta có các tỉ lệ thức sau( giả thiết các tỉ lệ thức phải chứng minh đều có nghĩa):a)dfrac{a-b}{a+b}dfrac{c-d}{c+d} b)dfrac{2a+5b}{3a-4b}dfrac{2c+5d}{3c-4d}c)dfrac{ab}{cd}dfrac{left(a-bright)^2}{left(c-dright)^2} d)dfrac{ac}{bd}dfrac{a^2+c^2}{b^2+d^2}ai hộ mik vs
Đọc tiếp
Bài 7: Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\). Chứng minh rằng ta có các tỉ lệ thức sau( giả thiết các tỉ lệ thức phải chứng minh đều có nghĩa):
a)\(\dfrac{a-b}{a+b}=\dfrac{c-d}{c+d}\) b)\(\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
c)\(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\) d)\(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)
ai hộ mik vs
a, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
b, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{2a}{2c}=\dfrac{5b}{5d}=\dfrac{3a}{4c}=\dfrac{4b}{4d}=\dfrac{2a+5b}{2c+5d}=\dfrac{3a-4b}{3c-4d}\Rightarrow\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
Đúng 3
Bình luận (0)
c, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2k}{d^2k}=\dfrac{b^2}{d^2}\)
\(\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}=\dfrac{\left(bk-b\right)^2}{\left(dk-d\right)^2}=\dfrac{b^2\left(k-1\right)^2}{d^2\left(k-1\right)^2}=\dfrac{b^2}{d^2}\)
Do đó \(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
d, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\)
\(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\)
Do đó \(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)
Đúng 2
Bình luận (0)
Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) . Chứng minh rằng ta có các tỉ lệ thức sau (giả thiết các tỉ lệ thức là có nghĩa ) :
a) \(\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\)
b) \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\)