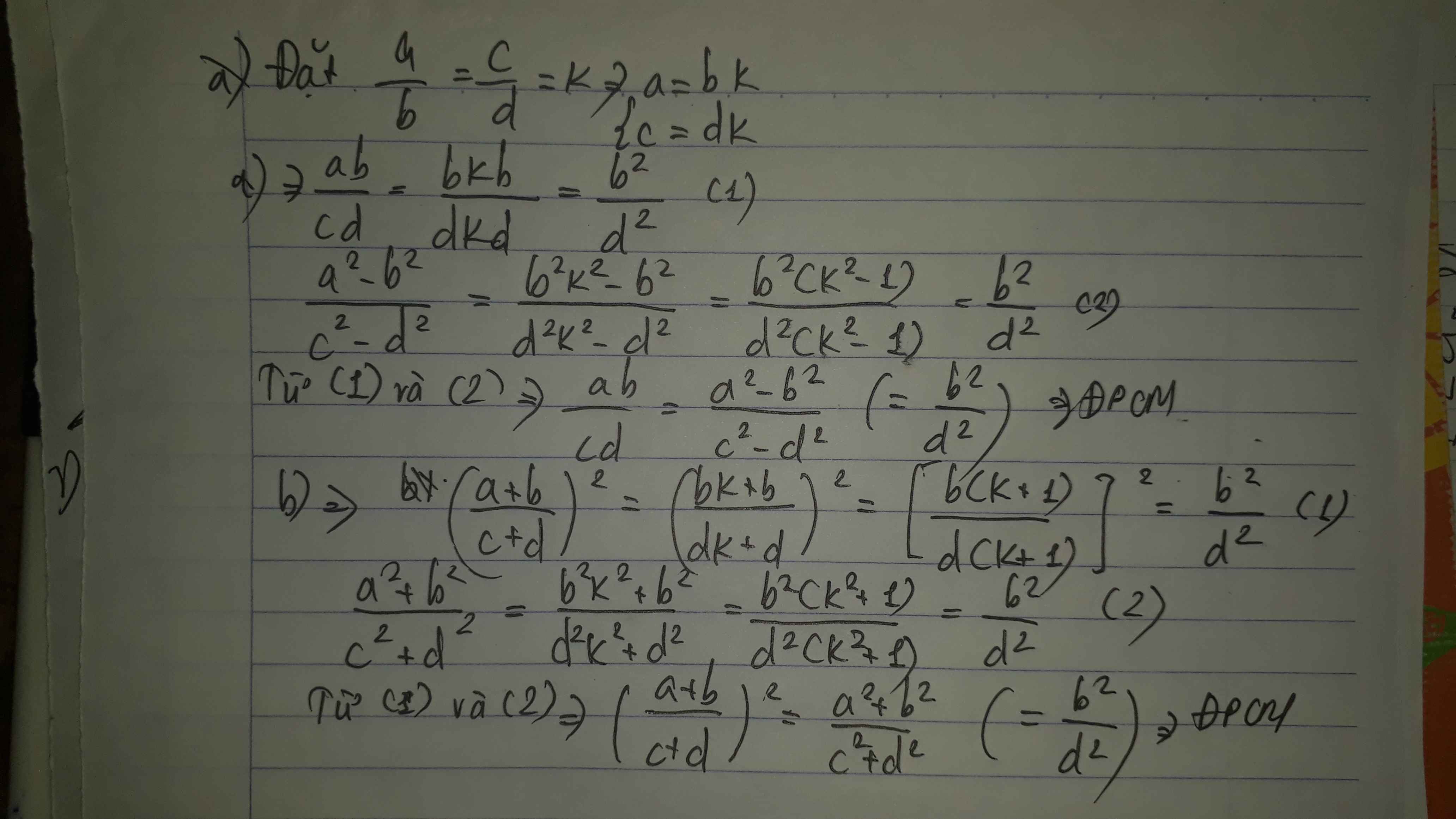9 tháng 8 2021 lúc 16:44
Violympic toán 7
Các câu hỏi tương tự
cho \(\dfrac{a}{b}=\dfrac{c}{d}\) chứng minh rằng tacos tỉ lệ thức sau (giả thiết các tỉ lệ thức đều có nghĩa ) \(\left(\dfrac{a+b}{c+d}\right)^3=\dfrac{a^3+b^3}{c^3+d^3}\)
Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\)
Chứng minh rằng \(\dfrac{a}{a-b}=\dfrac{c}{c-d}\)
bằng 3 các(giả thiết a khác b;c khác d và mỗi số a,b,c,d khác 0)
Cho tỉ lệ thức \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\) . CM các tỉ lệ thức sau :
a. \(\dfrac{a^2-b^2}{ab}\) = \(\dfrac{c^2-d^2}{cd}\)
b. \(\dfrac{(a+b)^2}{a^2+b^2}\) =\(\dfrac{(c+d)^2}{c^2+d^2}\)
Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}.CMR:\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\)
Cho \(\dfrac{a}{b}=\dfrac{c}{d}\). Chứng minh rằng \(\dfrac{ab}{cd}=\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}\) ( với giả thiết các tỉ số đều có nghĩa )
Cho tỉ lệ thức \(\dfrac{a}{a+b}=\dfrac{c}{c+d}\). Chứng minh rằng \(\dfrac{a}{b}=\dfrac{c}{d}\) (giả thiết các tỉ số đều có nghĩa)
Giúp với ạ ...
20 tháng 12 2017 lúc 20:19
Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}.CMR\)
a, \(\dfrac{a-b}{a+b}=\dfrac{c-d}{c+d}\)
b, \(\dfrac{7a-4b}{3a+5b}=\dfrac{7c-4d}{3c+5d}\)
c, \(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(c-a\right)^2}{\left(d-b\right)^2}\)
Cho \(\dfrac{a}{b}=\dfrac{c}{d}\). Chứng minh rằng \(\dfrac{ac}{bd}=\dfrac{a^2-c^2}{b^2-d^2}\) ( với giả thiết các tỉ số đều có nghĩa )
chứng minh tỉ lệ thức
\(\dfrac{a.b}{c.d}\)=\(\dfrac{a^2-b^2}{c^2-d^2}\)