tìm k để 3 đường thẳng sau đồng quy trong mặt phẳng tọa độ (d1):y=x+2,(d2):y=-2 và (d3):y=(k+1)x+k

Những câu hỏi liên quan
Cho 3 đường thẳng :
x + y = 1 (d1)
x - y =1 (d2)
(k+1)x + (k-1)y = k +1 với k 1 (d3)
Tìm các giá trị của k để:
a) (d1) và (d3) vuông góc với nhau
b) (d1),(d2),(d3) đồng quy tại 1 điểm trong mặt phẳng tọa độ Oxy
c) CMR: Đường thẳng (d3) luôn luôn đi qua 1 điểm cố định trong mặt phẳng tọa độ Oxy
\(\left(d_1\right):y=-x+1\)
\(\left(d_2\right):y=x-1\)
\(\left(d_3\right):y=\dfrac{k+1}{1-k}x+\dfrac{k+1}{k-1}\)
a) Để (d1) và (d3) vuông góc với nhau:
\(\Leftrightarrow\left(-1\right)\left(\dfrac{k+1}{1-k}\right)=-1\)\(\Leftrightarrow k=0\)(thỏa)
Vậy k=0
b)Giao điểm của (d1) và (d2) là nghiệm của hệ \(\left\{{}\begin{matrix}y=-x+1\\y=x-1\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}y=0\\x=1\end{matrix}\right.\)
Để (d1);(d2);(d3) đồng quy\(\Leftrightarrow\) (d3) đi qua điểm (1;0)
\(\Rightarrow0=\dfrac{k+1}{1-k}.1+\dfrac{k+1}{k-1}\)\(\Leftrightarrow0=0\)(lđ)
Vậy với mọi k thì (d1);d2);(d3) luôn cắt nhau tại một điểm
c)Gỉa sử \(M\left(x_0;y_0\right)\) là điểm cố định mà (d3) luôn đi qua
Khi đó \(\left(k+1\right)x_0+\left(k-1\right)y_0=k+1\) luôn đúng với mọi k
\(\Leftrightarrow k\left(x_0+y_0-1\right)+x_0-y_0-1=0\) luôn đúng với mọi k
\(\Leftrightarrow\left\{{}\begin{matrix}x_0+y_0-1=0\\x_0-y_0-1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=1\end{matrix}\right.\)
Vậy \(M\left(2;1\right)\) là điểm cố định mà (d3) luôn đi qua.
Đúng 3
Bình luận (0)
Trong mặt phẳng tọa độ Oxy xét ba đường thẳng có phương trình:
(d1): x-5y+k=0; (d2): (2k-3)x+k(y-1)=0; (d3): (k+1)x-y+1
Tìm các giá trị của tham số k để ba đường thẳng đó đồng quy
Tìm giá trị của k để 3 đường thẳng sau đồng quy tại một điểm trong mặt phẳng toạ độ:
a) y = 2x - 7 (d1); y = -x + 5 (d2); y = kx + 5 (d3)
b) y = kx - 7 (d1); y = 3x - 5 (d2); y = x - 1 (d3)
c) y = x - 7 (d1); y = kx - 3 (d2); y = 3x - 1 (d3)
a, ta có
(d1)=(d2)
2x-7=-x+5
\(\Leftrightarrow\)3x=12
\(\Leftrightarrow\)x=4
ta có
(d1)=(d3)
2x-7=kx+5
\(\Leftrightarrow\)2.4-7=k4+5
\(\Leftrightarrow\)k=-1
b, ta có
(d3)=(d2)
x-1=3x-5
\(\Leftrightarrow\)x=2
ta có
(d1)=(d3)
kx-7=x-1
\(\Leftrightarrow\)k2-7=2-1
\(\Leftrightarrow\)k=4
c, ta có
(d1)=(d3)
x-7=3x-1
\(\Leftrightarrow\)x=-3
ta có
(d1)=(d2)
x-7= kx-3
\(\Leftrightarrow\)-3-7=-3k-3
\(\Leftrightarrow\)k=\(\frac{7}{3}\)
Cho hàm số y=-x có đồ thị (D1) và hàm số y=2x-3 có đồ thị (D2)
a)Vẽ (D1), (D2) trên cùng một hệ trục tọa độ. Tìm tọa độ giao điểm của (D1), (D2) bằng phép toán
b)Cho (D3):y=(2k-1)x+3-k. Tìm k để (D1), (D2) và (D3) đồng quy
Cho 3 đường thẳng :
x + y 1 (d1)
x - y 1 (d2)
(k+1)x + (k-1)y k +1 với k ≠1 (d3)
Tìm các giá trị của k để:
a) (d1) và (d3) vuông góc với nhau
b) (d1),(d2),(d3) đồng quy tại 1 điểm trong mặt phẳng tọa độ Oxy
c) CMR: Đường thẳng (d3) luôn luôn đi qua 1 điểm cố định trong mặt phẳng tọa độ Oxy
Đọc tiếp
Cho 3 đường thẳng :
x + y = 1 (d1)
x - y =1 (d2)
(k+1)x + (k-1)y = k +1 với k ≠1 (d3)
Tìm các giá trị của k để:
a) (d1) và (d3) vuông góc với nhau
b) (d1),(d2),(d3) đồng quy tại 1 điểm trong mặt phẳng tọa độ Oxy
c) CMR: Đường thẳng (d3) luôn luôn đi qua 1 điểm cố định trong mặt phẳng tọa độ Oxy
a, (d1) y = -x + 1
(d3) y = \(\dfrac{k+1}{1-k}\) x -\(\dfrac{k+1}{1-k}\) ĐK k \(\ne\) 1
Để d1 \(\perp\) d3 \(\Leftrightarrow\) -1.\(\dfrac{k+1}{1-k}\) = -1 \(\Rightarrow\)k+1=1-k
\(\Rightarrow\) k = 0 (TM)
b, Xét pt hoành độ giao điểm của d1 và d2
x-1 = 1-x \(\Leftrightarrow\) x= 1 \(\Rightarrow\) y = 0
vậy A(1;0)
Để d1 , d2 và d3 đồng quy \(\Leftrightarrow\) A thuộc d3
thay A(1;0) vào d3 đc
0 = 0.k
Vậy vs mọi k\(\ne\) 1 thì d1,d2,d3 .....
c, Gọi B(xB;yB) là điểm cố định d3 luôn đi qua với mọi k khác 1
Ta có
k.xB+xB+k.yB-yB-k-1=0 đúng với mọi k\(\ne\)1
\(\Leftrightarrow\)k(xB+yB-1)+(xB-yB-1) =0 đúng với ...
\(\Rightarrow\left\{{}\begin{matrix}x_B+y_B=1\\x_B-y_B=1\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}x_B=1\\y_B=0\end{matrix}\right.\)
=> B(1;0) ...
Đúng 0
Bình luận (0)
Nguyễn Việt Lâm, Phùng Khánh Linh, Thiên Hàn, Khánh Như Trương Ngọc, Trần Trung Nguyên, Bonking, Nguyễn Thị Thảo Vy, KHUÊ VŨ, Phạm Tiến, Nigou Nguyễn , Mysterious Person, Mashiro Shiina, Nguyễn Thanh Hằng, Aki Tsuki, ...
Đúng 0
Bình luận (0)
Giúp mk với!!! Mình cần gấp lắm các pạn à!!!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1:Xác định m để ba đường thẳng sau: 1: y -2x, d2: y -x +1, d3 : y -(m +3)x - 2m +1 đồng quy.Bài 2: Trên cùng một mặt phẳng tọa độ cho hàm số d1 : y -2x và d2 : y x+3. a) Tìm tọa độ giao điểm của hai đường thẳng d1 và d2 bằng hai cách.b) Viết phương trình đường thẳng d3 biết đường thẳng này song song với d1 và cắt d2 tại điểm có hoành độ bằng 1.Bài 3 :Xác định các hệ số a, b biết đường thẳng d: y ax +b song song với đường thẳng d1 : y 3.x và cắt trục hoành tại điểm có hoành độ bằng 2/3
Đọc tiếp
Bài 1:Xác định m để ba đường thẳng sau:
1: y= -2x, d2: y = -x +1, d3 : y = -(m +3)x - 2m +1 đồng quy.
Bài 2: Trên cùng một mặt phẳng tọa độ cho hàm số d1 : y = -2x và d2 : y = x+3. a) Tìm tọa độ giao điểm của hai đường thẳng d1 và d2 bằng hai cách.
b) Viết phương trình đường thẳng d3 biết đường thẳng này song song với d1 và cắt d2 tại điểm có hoành độ bằng 1.
Bài 3 :Xác định các hệ số a, b biết đường thẳng d: y ax +b song song với đường thẳng d1 : y = 3.x và cắt trục hoành tại điểm có hoành độ bằng 2/3
Bài 3:
Vì (d)//(d1) nên a=3
Vậy: (d): y=3x+b
Thay \(x=\dfrac{2}{3}\) và y=0 vào (d), ta được:
\(b+2=0\)
hay b=-2
Đúng 0
Bình luận (1)
trên mặt phẳng tọa độ Oxy, cho 3 đường thẳng có phương trình:
(d1) : y=4x+4
(d2) : y=2x+2
(d3) : y=(3m+5)x+m-1 (m là tham số)
xác định m để 3 đường thẳng (d1),(d2),(d3) đồng quy
\(PT\text{ hoành độ giao điểm }\left(d_1\right);\left(d_2\right)\\ 4x+4=2x+2\Leftrightarrow x=-1\Leftrightarrow y=0\Leftrightarrow A\left(-1;0\right)\\ \text{Đồng quy }\Leftrightarrow A\left(-1;0\right)\in\left(d_3\right)\Leftrightarrow-3m-5+m-1=0\Leftrightarrow-2m-6=0\Leftrightarrow m=-3\)
Đúng 1
Bình luận (0)
Cho ( d1): y = x – 2 , ( d2): y = - 2x + 4
a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ. b) Tìm m và k của (d3) y = (m + 2)x + 2k - 7 biết (d3) // (d1)
c) Tìm m và k của (d4) y = (4 - 2m)x + k +1 biết (d4) cắt (d1) tại một điểm trên trục tung
d) Tìm m và k của (d5) y = (3m - 1)x + 4k - 3 biết (d5) trùng (d1)
c: Vì (d4) cắt (d1) tại một điểm trên trục tung nên k+1=-2
hay k=-3
Đúng 2
Bình luận (0)
Câu 2. Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d1):y=2x và đường thẳng (d2):y=-x+2. a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ. b) Cho đường thẳng (d3):y=ax+b Xác định a,b biết rằng đường thẳng (d3) song song với đường thẳng (d2) đồng thời cắt đường thẳng (d1) tại điểm có hoành độ bằng 1.
a: 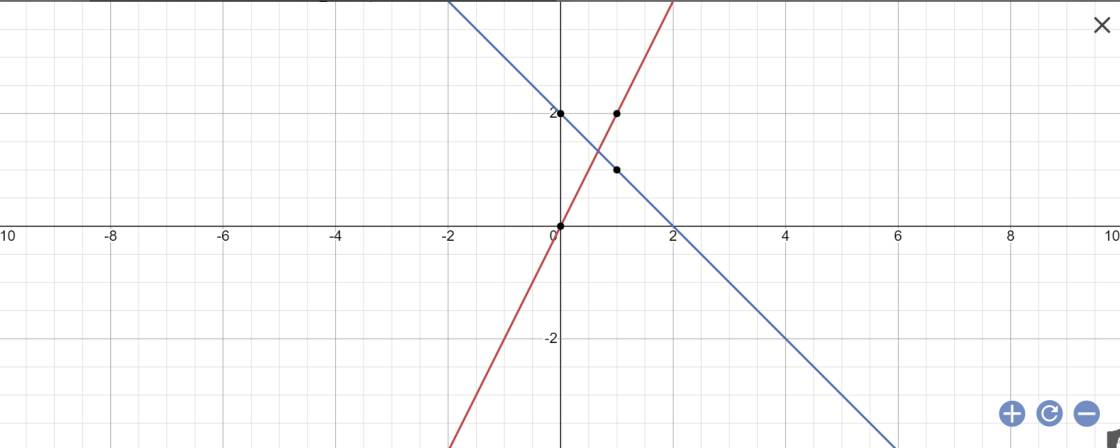
b: Vì (d3)//(d2) nên \(\left\{{}\begin{matrix}a=-1\\b\ne2\end{matrix}\right.\)
Vậy: (d3): y=-x+b
Thay x=1 vào (d1), ta được:
\(y=2\cdot1=2\)
Thay x=1 và y=2 vào y=-x+b, ta được:
\(b-1=2\)
=>b=2+1=3
Đúng 0
Bình luận (0)

















