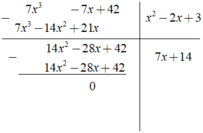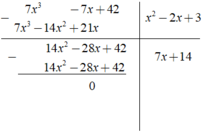x.( 7x - 42 ) + 10. ( 7x - 42 ) = 0

=> ( 7x - 42 ). ( x + 10 ) = 0

=> \(\orbr{\begin{cases}x+10=0\\7x-42=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=-10\\x=6\end{cases}}\)

Ta có: 7x=3y=2z

nên \(\dfrac{x}{\dfrac{1}{7}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{2}}\)

hay \(\dfrac{7x}{1}=\dfrac{3y}{1}=\dfrac{4z}{2}\)

mà 7x-3y+4z=42

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{7x}{1}=\dfrac{3y}{1}=\dfrac{4z}{2}=\dfrac{7x-3y+4z}{1-1+2}=\dfrac{42}{2}=21\)

Do đó:x=3; y=7; z=10,5

\(\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{49x^2+7x-42}=181-14x\) ( ĐK : \(\frac{6}{7}\le x\le\frac{181}{14}\))

\(\Leftrightarrow\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{\left(7x+7\right)\left(7x-6\right)}=-\left(7x+7\right)-\left(7x-6\right)+182\)

Đặt \(\left\{{}\begin{matrix}\sqrt{7x+7}=a\left(a\ge0\right)\\\sqrt{7x-6}=b\left(b\ge0\right)\end{matrix}\right.\)

\(\Leftrightarrow a+b+2ab=-a^2-b^2+182\)

\(\Leftrightarrow\left(a+b\right)^2+\left(a+b\right)-182=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a+b=13\left(N\right)\\a+b=-14\left(L\right)\end{matrix}\right.\)

\(\Rightarrow\sqrt{7x+7}+\sqrt{7x-6}=13\)

\(\Leftrightarrow\sqrt{49x^2+7x-42}=84-7x\)

\(\Leftrightarrow49x^2+7x-42=49x^2-1176x+7056\)

\(\Leftrightarrow1183x=7098\)

\(\Leftrightarrow x=6\left(TM\right)\)

Vậy S={6}

\(\sqrt{7x+7}+\sqrt{7x-6}=t\ge0\)

\(bpt\Leftrightarrow t+t^2< 182\Leftrightarrow-14< t< 13\Leftrightarrow t< 13\Leftrightarrow\sqrt{7x+7}+\sqrt{7x-6}< 13\left(đk:x\ge\dfrac{6}{7}\right)\Leftrightarrow14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 169\Leftrightarrow2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 168-14x\Leftrightarrow\left\{{}\begin{matrix}\left(7x+7\right)\left(7x-6\right)\ge0\\168-14x\ge0\\4\left(7x+7\right)\left(7x-6\right)< \left(168-14x\right)^2\end{matrix}\right.\)

\(giảibpt\Rightarrowđáp\) \(số\)

Có: \(-7x=14y\)

=> \(\frac{14}{x}=\frac{-7}{y}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\frac{14}{x}=\frac{-7}{y}=\frac{2\cdot14-7}{2x+y}=\frac{21}{42}=\frac{1}{2}\)

\(\Rightarrow\begin{cases}\frac{14}{x}=\frac{1}{2}\\-\frac{7}{y}=\frac{1}{2}\end{cases}\)\(\Leftrightarrow\begin{cases}x=28\\y=-14\end{cases}\)

Giải:

Ta có: \(-7x=14y\Rightarrow\frac{x}{14}=\frac{y}{-7}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\frac{x}{14}=\frac{y}{-7}=\frac{2x}{28}=\frac{y}{-7}=\frac{2x+y}{28+\left(-7\right)}=\frac{42}{21}=2\)

+) \(\frac{x}{14}=2\Rightarrow x=28\)

+) \(\frac{y}{-7}=2\Rightarrow y=-14\)

Vậy cặp số \(\left(x,y\right)\) là \(\left(28,-14\right)\)

7x + 14 = 42

7x         = 42 - 14

7x         = 28

  x         = 28 : 7

  x         = 4

Vậy x = 4

7x = 42 - 14 

7x = 28

x = 28 : 7

x = 4

7x=42-14

7x=28

x=28:7

x=4

Ta có phép chia

Chọn đáp án B.

Ta có phép chia

Chọn đáp án B.

\(a,\Rightarrow x=150-23=127\\ b,\Rightarrow300:x=42+18=60\\ \Rightarrow x=300:60=5\\ c,\Rightarrow7^{x+3}=7^{23+8}=7^{31}\\ \Rightarrow x+3=31\Rightarrow x=28 \)

a) \(\Rightarrow x=150-23\)

\(\Rightarrow x=127\)

b) \(\Rightarrow300:x=60\)

\(\Rightarrow x=5\)

c) \(\Rightarrow7^{x+3}=7^{31}\)

\(\Rightarrow x+3=31\Rightarrow x=28\)

a.x=127

b x=5

c x=7^28

\(7x^2-35x+42\)

Đặt \(7x^2-35x+42=0\)

\(\Leftrightarrow7.\left(x^2-5x+6\right)=0\)

\(\Leftrightarrow7.\left(x^2-2x-3x+6\right)=0\)

\(\Leftrightarrow7.\left[\left(x^2-2x\right)-\left(3x-6\right)\right]=0\)

\(\Leftrightarrow7.\left[x.\left(x-2\right)-3.\left(x-2\right)\right]=0\)

\(\Leftrightarrow7.\left(x-2\right).\left(x-3\right)=0\)

Vì \(7\ne0.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0+2\\x=0+3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)

Vậy \(x=2\) và \(x=3\) đều là nghiệm của đa thức \(7x^2-35x+42.\)

Chúc em học tốt!

Thiếu dữ kiện nhé!

7x2−35x+42=07x2−35x+42=0

⇔7(x2−5x+6)=0⇔7(x2−5x+6)=0

⇔7(x2−2x−3x+6)⇔7(x2−2x−3x+6)

⇔7[x(x−2)−3(x−2)]⇔7[x(x−2)−3(x−2)]

⇔7(x−3)(x−2)=0⇔7(x−3)(x−2)=0

⇔⎡⎣⎢7=0x−3=0x−2=0

⇔7=0 , x-3=0; x-2=0

⇔⎡⎣⎢x∈∅x=3x=2⇔[x∈∅x=3x=2

Vậy x = 3 hoặc x = 2