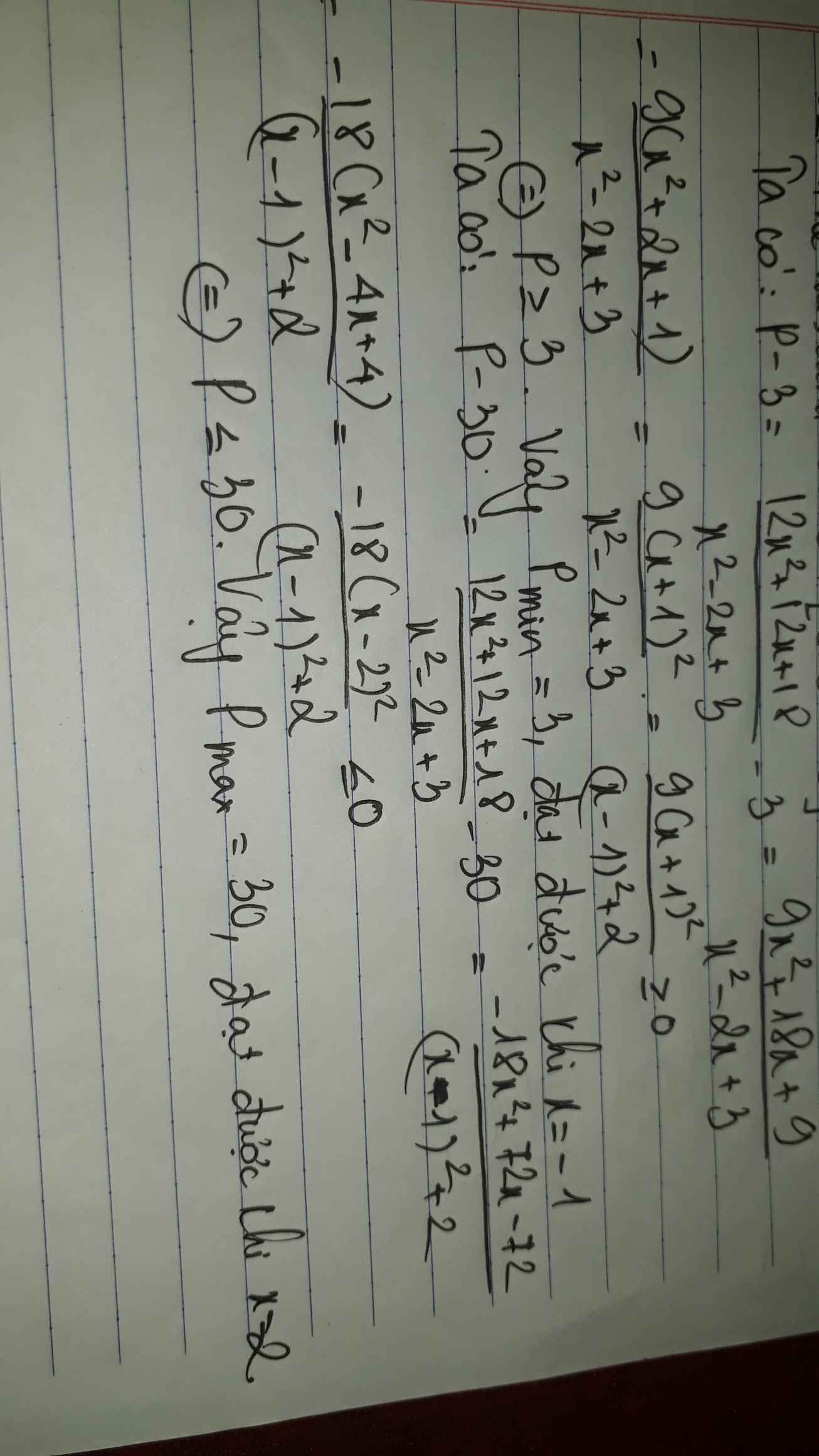\(A=\dfrac{27-12x}{x^2+9}=\dfrac{x^2-12x+36-\left(x^2+9\right)}{x^2+9}=\dfrac{\left(x-6\right)^2}{x^2+9}-1\ge-1\)

\(A_{min}=-1\Leftrightarrow x=6\)

\(A=\dfrac{27-12x}{x^2+9}=\dfrac{4\left(x^2+9\right)-\left(4x^2+12x+9\right)}{x^2+9}=4-\dfrac{\left(2x+3\right)^2}{x^2+9}\le4\)

\(A_{max}=4\Leftrightarrow x=\dfrac{-3}{2}\)

\(A=\dfrac{27-12x}{x^2+9}=\dfrac{x^2+9+27-12x}{x^2+9}-1=\dfrac{x^2-12x+36}{x^2+9}-1=\dfrac{\left(x-6\right)^2}{x^2+9}-1\ge-1\)

Dấu = xảy ra khi x = 6

Vậy:...

A= \(\dfrac{27-12x}{x^2-9}\)

= \(\dfrac{x^2-12x+36-x^2-9}{x^2-9}\)

= \(\dfrac{\left(x-6\right)^2-\left(x^2+9\right)}{x^2+9}\)

= \(\dfrac{\left(x-6\right)^2}{x^2+9}-1\)

Ta có \(\dfrac{\left(x-6\right)^2}{x^2+9}\) ≥ 0 ∀ x

⇒ \(\dfrac{\left(x-6\right)^2}{x^2+9}-1\) ≥ -1 ∀ x

Vậy A_Min= -1 tại x=6

1) Xét rằng x > 7 <=> A < 0

Lại xét x < 7 thì mẫu là một số nguyên dương. P/s A có tử và mẫu đều là số dương, mà tử lại bất biến

A(max) <=> mẫu 7 - x nhỏ nhất <=> 7 - x = 1 => x = 7 - 1 = 6 <=> A = 1

Từ những điều trên thì A sẽ có GTLN khi và chỉ khi x = 6

a, \(A=-x^2-2x+3=-\left(x^2+2x-3\right)=-\left(x^2+2x+1-4\right)\)

\(=-\left(x+1\right)^2+4\le4\)

Dấu ''='' xảy ra khi x = -1 

Vậy GTLN là 4 khi x = -1 

b, \(B=-4x^2+4x-3=-\left(4x^2-4x+3\right)=-\left(4x^2-4x+1+2\right)\)

\(=-\left(2x-1\right)^2-2\le-2\)

Dấu ''='' xảy ra khi x = 1/2 

Vậy GTLN B là -2 khi x = 1/2 

c, \(C=-x^2+6x-15=-\left(x^2-2x+15\right)=-\left(x^2-2x+1+14\right)\)

\(=-\left(x-1\right)^2-14\le-14\)

Vâỵ GTLN C là -14 khi x = 1

Bài 8 : 

b, \(B=x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\)

Dấu ''='' xảy ra khi x = 3

Vậy GTNN B là 2 khi x = 3 

c, \(x^2-x+1=x^2-x+\dfrac{1}{4}+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)

Dấu ''='' xảy ra khi x = 1/2 

Vậy ...

c, \(x^2-12x+2=x^2-12x+36-34=\left(x-6\right)^2-34\ge-34\)

Dấu ''='' xảy ra khi x = 6

Vậy ...

Ai lm đc câu nào thì giúp mk với , cảm ơn !!

\(A=\left|\dfrac{3}{5}-x\right|+\dfrac{1}{9}\ge\dfrac{1}{9}\\ A_{min}=\dfrac{1}{9}\Leftrightarrow x=\dfrac{3}{5}\\ B=\dfrac{2009}{2008}-\left|x-\dfrac{3}{5}\right|\le\dfrac{2009}{2008}\\ B_{max}=\dfrac{2009}{2008}\Leftrightarrow x=\dfrac{3}{5}\\ C=-2\left|\dfrac{1}{3}x+4\right|+1\dfrac{2}{3}\le1\dfrac{2}{3}\\ C_{max}=1\dfrac{2}{3}\Leftrightarrow\dfrac{1}{3}x=-4\Leftrightarrow x=-12\)

a: \(A=\left|\dfrac{3}{5}-x\right|+\dfrac{1}{9}\ge\dfrac{1}{9}\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{3}{5}\)

Lời giải:

$y=\frac{x^2+3}{x^2-x+2}$
$\Leftrightarrow y(x^2-x+2)=x^2+3$

$\Leftrightarrow x^2(y-1)-xy+(2y-3)=0(*)$

Coi đây là pt bậc 2 ẩn $x$. Vì $y$ tồn tại nên $(*)$ luôn có nghiệm

$\Rightarrow \Delta=y^2-4(y-1)(2y-3)\geq 0$

$\Leftrightarrow -7y^2+20y-12\geq 0$

$\Leftrightarrow (7y-6)(2-y)\geq 0$

$\Leftrightarrow \frac{6}{7}\leq y\leq 2$

Vậy $y_{\min}=\frac{6}{7}; y_{\max}=2$