Cho \(1\le x;y;z\le\frac{4}{3}\)
chứng minh rằng \(xy\sqrt{4-3z}+yz\sqrt{4-3x}+xz\sqrt{4-3y}\le x^3+y^3+z^3\)
Những câu hỏi liên quan
cho cặp số (x,y) thỏa mãn các điều kiện :
-1≤x+y≤1,-1≤xy+x+y ≤1
cmr : |x|≤2 , |y|≤2
a)cho 1 ≤a ≤ 2 . c/m a+\(\frac{2}{a}\le3\)
b) cho x,y,z thỏa mãn 1 ≤ x ≤ y ≤ z ≤ 2
c/m (x+y+z) \(\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\le\frac{81}{8}\)
a)Cho hai số không âm x, y thỏa x,y \(\le\)1.CMR:
\(\frac{1}{1+x}+\frac{1}{1+y}\le\frac{2}{1+\sqrt{xy}}\)
b) Cho x,y,z,t thỏa 0\(\le x\le y\le z\le t\)và yt\(\le\)1.Chưng minh rằng:
\(\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}+\frac{1}{1+t}\le\frac{4}{1+\sqrt[4]{xyzt}}\)
a/ \(\frac{1}{1+x}+\frac{1}{1+y}\le\frac{2}{1+\sqrt{xy}}\)
\(\Leftrightarrow\left(1+x\right)\left(1+\sqrt{xy}\right)+\left(1+y\right)\left(1+\sqrt{xy}\right)-2\left(1+x\right)\left(1+y\right)\le0\)
\(\Leftrightarrow x\sqrt{xy}+2\sqrt{xy}+y\sqrt{xy}-x-y-2xy\le0\)
\(\Leftrightarrow\sqrt{xy}\left(x-2\sqrt{xy}+y\right)-\left(x-2\sqrt{xy}+y\right)\le0\)
\(\Leftrightarrow\left(\sqrt{x}-\sqrt{y}\right)^2\left(\sqrt{xy}-1\right)\le0\) đúng vì \(x,y\le1\)
b/ Vì \(\hept{\begin{cases}0\le x\le y\le z\le t\\yt\le1\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}xz\le1\\yt\le1\end{cases}}\)
Áp dụng câu a ta được
\(\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}+\frac{1}{1+t}\le\frac{2}{1+\sqrt{xz}}+\frac{2}{1+\sqrt{yt}}\le\frac{4}{1+\sqrt[4]{xyzt}}\)
Đúng 0
Bình luận (0)
[1] Cho các tập hợp A [ -5; dfrac{1}{2} ]; B ( -3; +infty ). Khi đó tập hợp Acap B bằng:A. { x ∈ R | -3 le xledfrac{1}{2} } B. { x ∈ R | - 3 x ledfrac{1}{2} } C. { x ∈ R | -5 x ledfrac{1}{2} } D. { x ∈ R | -3 le x dfrac{1}{2}}
Đọc tiếp
[1] Cho các tập hợp A = [ -5; \(\dfrac{1}{2}\) ]; B = ( -3; \(+\infty\) ). Khi đó tập hợp \(A\cap B\) bằng:
A. { x ∈ R | -3 \(\le x\le\dfrac{1}{2}\) } B. { x ∈ R | - 3 < x \(\le\dfrac{1}{2}\) } C. { x ∈ R | -5 < x \(\le\dfrac{1}{2}\) } D. { x ∈ R | -3 \(\le x< \dfrac{1}{2}\)}
Ta có:
Tập hợp A:
\(A=\left[-5;\dfrac{1}{2}\right]\)
Tập hợp B:
\(B=\left(-3;+\infty\right)\)
Mà: \(A\cap B\)
\(\Rightarrow\left\{x\in R|-3\le x\le\dfrac{1}{2}\right\}\)
⇒ Chọn A
Đúng 2
Bình luận (0)
cho hàm số y=f(x)= -x2 với -2≤x≤-1 thì -4≤f(x)≤1
Giúp e với ak
cho 3 số nguyên dương 0 ≤ x ≤ y ≤ z ≤1 chứng minh:
\(\dfrac{x}{yz+1}+\dfrac{y}{xz+1}+\dfrac{z}{xy+1}\)≤2
Cho số thực x thỏa mãn 0≤x≤1. Chứng minh x2≤x
Xét hiệu:
\(x^2-x=x\left(x-1\right)\)
Mà \(0\le x\le1\Rightarrow x\ge0;x-1\le0\)
\(\Rightarrow x\left(x-1\right)\le0\)
\(\Rightarrow x^2-x\le0\Leftrightarrow x^2\le x\)
Giải mục 1 trang 80, 81 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 13:57
Cho hàm số y fleft( x right) left{ {begin{array}{*{20}{c}}1&{khi,,0 le x le 1}{1 + x}&{khi,,1 x le 2}{5 - x}&{khi,,2 x le 3}end{array}} right. có đồ thị như Hình 1.Tại mỗi điểm {x_0} 1 và {x_0} 2, có tồn tại giới hạn mathop {lim }limits_{x to {x_0}} fleft( x right) không? Nếu có, giới hạn đó có bằng fleft( {{x_0}} right) không?
Đọc tiếp
Cho hàm số \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}1&{khi\,\,0 \le x \le 1}\\{1 + x}&{khi\,\,1 < x \le 2}\\{5 - x}&{khi\,\,2 < x \le 3}\end{array}} \right.\) có đồ thị như Hình 1.
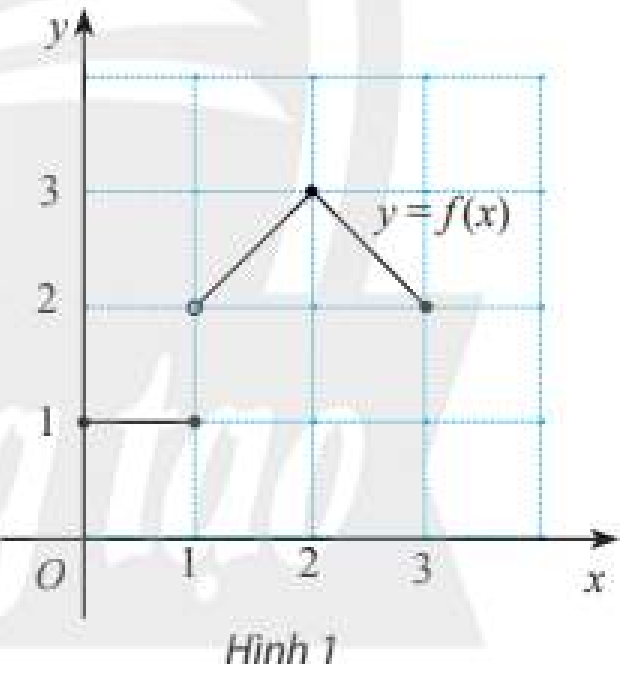
Tại mỗi điểm \({x_0} = 1\) và \({x_0} = 2\), có tồn tại giới hạn \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) không? Nếu có, giới hạn đó có bằng \(f\left( {{x_0}} \right)\) không?
• \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {1 + x} \right) = 1 + 1 = 2\).
\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} 1 = 1\).
Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).
• \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {5 - x} \right) = 5 - 2 = 3\).
\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {1 + x} \right) = 1 + 2 = 3\).
Vì \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} {\rm{ }}f\left( x \right) = 3\) nên \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 3\).
Ta có: \(f\left( 2 \right) = 1 + 2 = 3\).
Vậy \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = f\left( 2 \right)\).
Đúng 0
Bình luận (0)
Cho 3 số dương 0\(\le x\le y\le z\le\)1. Chứng minh rằng:
\(\frac{x}{yz+1}+\frac{y}{xz+1}+\frac{z}{xy+1}\le2\)
Câu hỏi của Kaitou Kid(Kid-sama) - Toán lớp 7 . Bạn check thử cái cách "Bài này lớp 7 dư sức giải..." nhé! Mình đọc nhiều đề thi hsg để tự luyện thấy lời giải của họ như vậy (không có chỗ dấu "=" xảy ra nha,cái chỗ này mình tự thêm) .Không biết đúng hay sai.Còn mấy cách kia là mình tự làm nhé!
Đúng 0
Bình luận (0)
1) cho góc x (0 độ le x 90 độ) thỏa mãn sinxdfrac{4}{5} giá trị của tanx là 2) cho góc x (0 độ le x le 180 độ) thỏa mãn cosxdfrac{1}{3} giá trị của sinx là3) cho cosxdfrac{1}{2} tính P3sin^2x+4cos^2x
Đọc tiếp
1) cho góc x (0 độ \(\le\) x < 90 độ) thỏa mãn \(sinx=\dfrac{4}{5}\) giá trị của \(tanx\) là
2) cho góc x (0 độ \(\le\) x \(\le\) 180 độ) thỏa mãn \(cosx=\dfrac{1}{3}\) giá trị của \(sinx\) là
3) cho \(cosx=\dfrac{1}{2}\) tính \(P=3sin^2x+4cos^2x\)
