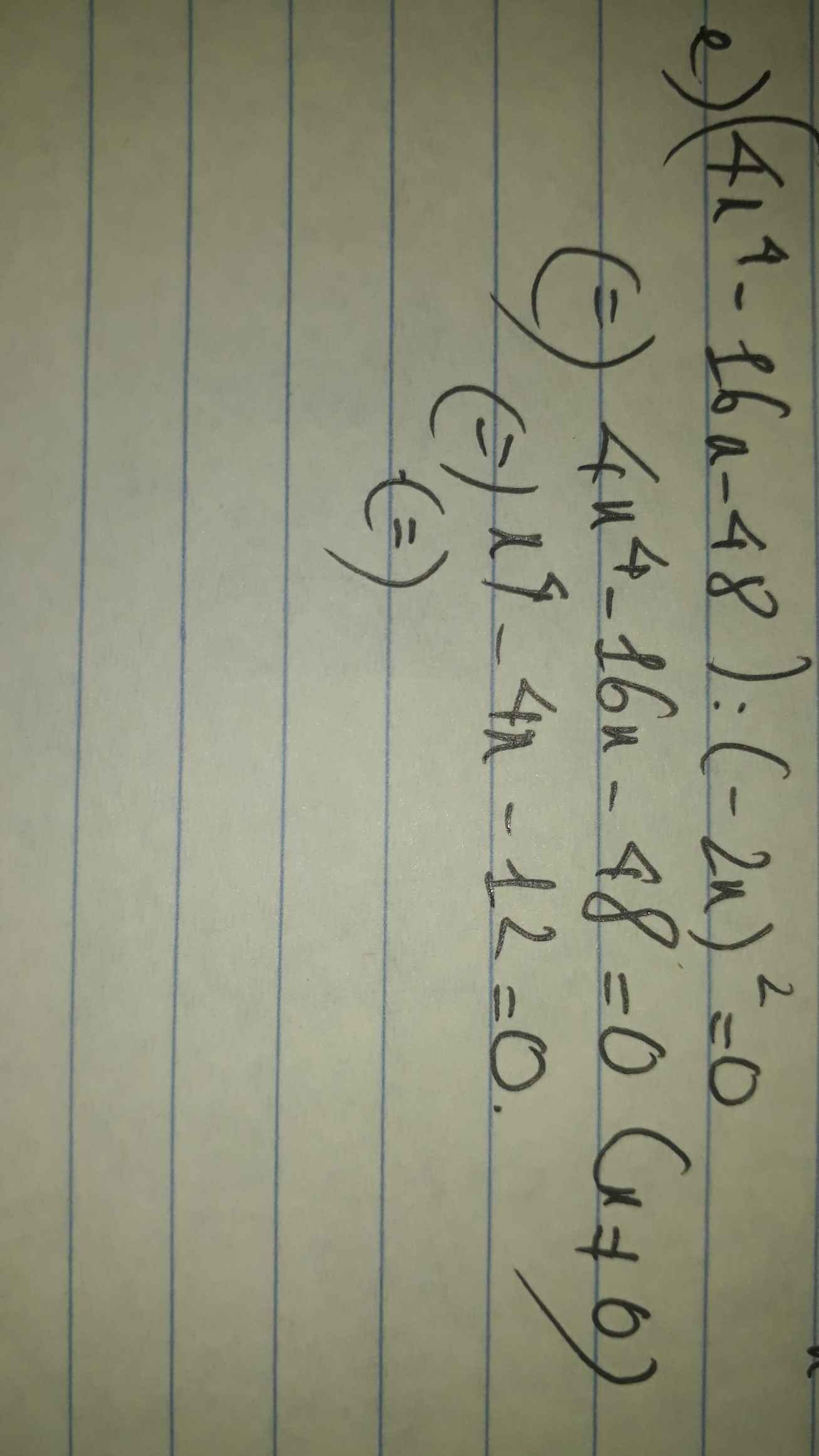1. a) \(7x^2\left(2x^3+3x^5\right)=7x^2\cdot2x^3+7x^2\cdot3x^5=14x^5+21x^7\)

b) \(\left(x^3-x^2+x-1\right):\left(x-1\right)=\dfrac{x^3-x^2+x-1}{x-1}\)

\(=\dfrac{x^2\left(x-1\right)+\left(x-1\right)}{x-1}=\dfrac{\left(x-1\right)\left(x^2+1\right)}{x-1}=x^2+1\)

2: \(x^2-8x+7=0\)

=>\(x^2-x-7x+7=0\)

=>\(x\left(x-1\right)-7\left(x-1\right)=0\)

=>\(\left(x-1\right)\left(x-7\right)=0\)

=>\(\left[{}\begin{matrix}x-1=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=7\end{matrix}\right.\)

1:

a: \(7x^2\left(2x^3+3x^5\right)=7x^2\cdot2x^3+7x^2\cdot3x^5=21x^7+14x^5\)

b: \(\dfrac{x^3-x^2+x-1}{x-1}=\dfrac{x^2\left(x-1\right)+\left(x-1\right)}{\left(x-1\right)}\)

\(=x^2+1\)

1)

\(a,7x^2\cdot(2x^3+3x^5)\\=7x^2\cdot2x^3+7x^2\cdot3x^5\\=14x^5+21x^7\\---\\b,(x^3-x^2+x-1):(x-1)(dkxd:x\ne 1)\\=[x^2(x-1)+(x-1)]:(x-1)\\=(x-1)(x^2+1):(x-1)\\=x^2+1\)

2)

\(x^2-8x+7=0\\\Leftrightarrow x^2-x-7x+7=0\\\Leftrightarrow x(x-1)-7(x-1)=0\\\Leftrightarrow (x-1)(x-7)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=7\end{matrix}\right.\)

\(\text{#}Toru\)

a: Ta có: \(x\left(2-x\right)+\left(x^2+x\right)=7\)

\(\Leftrightarrow2x-x^2+x^2+x=7\)

\(\Leftrightarrow3x=7\)

hay \(x=\dfrac{7}{3}\)

b: Ta có: \(\left(2x+1\right)^2-x\left(4-5x\right)=17\)

\(\Leftrightarrow4x^2+4x+1-4x+5x^2=17\)

\(\Leftrightarrow9x^2=16\)

\(\Leftrightarrow x^2=\dfrac{16}{9}\)

hay \(x\in\left\{\dfrac{4}{3};-\dfrac{4}{3}\right\}\)

c: Ta có: \(\left(x-4\right)^2-\left(2x+1\right)^2=0\)

\(\Leftrightarrow\left(x-4-2x-1\right)\left(x-4+2x+1\right)=0\)

\(\Leftrightarrow\left(x+5\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)

d: ta có: \(\dfrac{2x^3-8x^2+10x}{2x}=0\)

\(\Leftrightarrow x^2-4x+5=0\)

\(\Leftrightarrow\left(x-2\right)^2+1=0\)(vô lý)

Câu 9: D

Câu 10: A

f'(x)=2*3x^2+3*2*(a+2)*x+6a^2

=6x^2+6x(a+2)+6a^2

Δ=(6a+12)^2-4*6*6a^2

=36a^2+144a+144-144a^2

=-108a^2+144a+144

f'(x)>0 với mọi x

=>-108a^2+144a+144<0

=>a<-2/3; a>2

f'(-1)=6

=>6*(-1)^2+6*(-1)*(a+2)+6a^2=6

=>6a^2+6-6a-12=6

=>6a^2-6a-12=0

=>a^2-a-2=0

=>a=2(loại) hoặc a=-1(nhận)

b: 4x^2-20x+25=(x-3)^2

=>(2x-5)^2=(x-3)^2

=>(2x-5)^2-(x-3)^2=0

=>(2x-5-x+3)(2x-5+x-3)=0

=>(3x-8)(x-2)=0

=>x=8/3 hoặc x=2

c: x+x^2-x^3-x^4=0

=>x(x+1)-x^3(x+1)=0

=>(x+1)(x-x^3)=0

=>(x^3-x)(x+1)=0

=>x(x-1)(x+1)^2=0

=>\(x\in\left\{0;1;-1\right\}\)

d: 2x^3+3x^2+2x+3=0

=>x^2(2x+3)+(2x+3)=0

=>(2x+3)(x^2+1)=0

=>2x+3=0

=>x=-3/2

a: =>x^2(5x-7)-3(5x-7)=0

=>(5x-7)(x^2-3)=0

=>\(x\in\left\{\dfrac{7}{5};\sqrt{3};-\sqrt{3}\right\}\)

a) Ta có: \(2-x=2\left(x-2\right)^3\)

\(\Leftrightarrow-\left(x-2\right)-2\left(x-2\right)^3=0\)

\(\Leftrightarrow\left(x-2\right)\left[1+2\left(x-2\right)^2\right]=0\)

\(\Leftrightarrow x-2=0\)

hay x=2

b) Ta có: \(8x^3-72x=0\)

\(\Leftrightarrow8x\left(x^2-9\right)=0\)

\(\Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)

Vậy: S={0;3;-3}

c) Ta có: \(\left(x-1.5\right)^6+2\left(1.5-x\right)^2=0\)

\(\Leftrightarrow\left(x-1.5\right)^2\left[\left(x-1.5\right)^4+2\right]=0\)

\(\Leftrightarrow x-1.5=0\)

hay x=1,5

d) Ta có: \(2x^3+3x^2+3+2x=0\)

\(\Leftrightarrow x^2\left(2x+3\right)+\left(2x+3\right)=0\)

\(\Leftrightarrow2x+3=0\)

\(\Leftrightarrow2x=-3\)

hay \(x=-\dfrac{3}{2}\)

e) Ta có: \(x^2\left(x+1\right)-x\left(x+1\right)+x\left(x-1\right)=0\)

\(\Leftrightarrow x\left(x+1\right)\left(x-1\right)+x\left(x-1\right)=0\)

\(\Leftrightarrow x\left(x-1\right)\left(x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)

Vậy: S={0;1;-2}

f) Ta có: \(x^3-4x-14x\left(x-2\right)=0\)

\(\Leftrightarrow x\left(x-2\right)\left(x+2\right)-14x\left(x-2\right)=0\)

\(\Leftrightarrow x\left(x-2\right)\left(x-12\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=12\end{matrix}\right.\)

Vậy: S={0;2;12}

ĐKXĐ: \(x\ge0\)

\(\left(x^2-x-m\right)\sqrt{x}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-x-m=0\left(1\right)\end{matrix}\right.\)

Giả sử (1) có nghiệm thì theo Viet ta có \(x_1+x_2=1>0\Rightarrow\left(1\right)\) luôn có ít nhất 1 nghiệm dương nếu có nghiệm

Do đó:

a. Để pt có 1 nghiệm \(\Leftrightarrow\left(1\right)\) vô nghiệm 

\(\Leftrightarrow\Delta=1+4m< 0\Leftrightarrow m< -\dfrac{1}{4}\)

b. Để pt có 2 nghiệm pb 

TH1: (1) có 1 nghiệm dương và 1 nghiệm bằng 0

\(\Leftrightarrow m=0\)

TH2: (1) có 2 nghiệm trái dấu

\(\Leftrightarrow x_1x_2=-m< 0\Leftrightarrow m>0\)

\(\Rightarrow m\ge0\)

c. Để pt có 3 nghiệm pb \(\Leftrightarrow\) (1) có 2 nghiệm dương pb

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=1+4m>0\\x_1x_2=-m>0\\\end{matrix}\right.\) \(\Leftrightarrow-\dfrac{1}{4}< m< 0\)

\(A-\left(x^2+y^2-4xy\right)=x^2+4xy+3x^2\)

\(\Leftrightarrow A=x^2+4xy+3x^2+x^2+y^2-4xy\)

\(\Leftrightarrow A=5x^2+y^2\)

\(B+\left(-x^4+x^2-2x^3-\dfrac{1}{3}\right)=3x^2-2x^3+x-\dfrac{2}{3}\)

\(\Leftrightarrow B=3x^2-2x^3+x-\dfrac{2}{3}+x^4-x^2+2x^3+\dfrac{1}{3}\)

\(\Leftrightarrow B=x^4+2x^2+x-\dfrac{1}{3}\)

A=5x²+y².

B=x⁴+2x²+x-1/3.

a: (2x+1)(3-x)(4-2x)=0

=>(2x+1)(x-3)(x-2)=0

hay \(x\in\left\{-\dfrac{1}{2};3;2\right\}\)

b: 2x(x-3)+5(x-3)=0

=>(x-3)(2x+5)=0

=>x=3 hoặc x=-5/2

c: =>(x-2)(x+2)+(x-2)(2x-3)=0

=>(x-2)(x+2+2x-3)=0

=>(x-2)(3x-1)=0

=>x=2 hoặc x=1/3

d: =>(x-2)(x-3)=0

=>x=2 hoặc x=3

e: =>(2x+5+x+2)(2x+5-x-2)=0

=>(3x+7)(x+3)=0

=>x=-7/3 hoặc x=-3

f: \(\Leftrightarrow2x^3+5x^2-3x=0\)

\(\Leftrightarrow x\left(2x^2+5x-3\right)=0\)

\(\Leftrightarrow x\left(x+3\right)\left(2x-1\right)=0\)

hay \(x\in\left\{0;-3;\dfrac{1}{2}\right\}\)

d: Ta có: \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)=24\)

\(\Leftrightarrow\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24=0\)

\(\Leftrightarrow x\left(x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)