Tìm GTNN của A = \(\dfrac{\left|x+2002\right|}{2003}\)

Những câu hỏi liên quan
Tính giá trị lớn nhất của:
A=\(\dfrac{2002}{\left|x\right|+2002}\)
B=\(\dfrac{\left|x\right|+2002}{-2003}\)
ĐK: \(x\in Z\)
a) Giải:
Để \(A\) đạt giá trị lớn nhất
\(\Leftrightarrow\dfrac{2002}{\left|x\right|+2002}\) đạt giá trị lớn nhất
\(\Leftrightarrow\left|x\right|+2002\) phải nhỏ nhất \(\Leftrightarrow\left|x\right|=0\)
\(\Rightarrow A_{Max}=\dfrac{2002}{0+2002}=\dfrac{2002}{2002}=1\)
Vậy giá trị lớn nhất của \(A\) là \(1\)
b) Để \(B\) đạt giá trị lớn nhất
\(\Leftrightarrow\dfrac{\left|x\right|+2002}{-2003}\) phải lớn nhất
Vì \(\left\{{}\begin{matrix}\left|x\right|+2002>0\\-2003< 0\end{matrix}\right.\)\(\Rightarrow\dfrac{\left|x\right|+2002}{-2003}< 0\)
Mà \(\forall-a< 0\) nếu muốn \(-a\) lớn nhất \(\Leftrightarrow a\) nhỏ nhất
\(\Leftrightarrow\left|x\right|+2002\) phải nhỏ nhất \(\Leftrightarrow\left|x\right|=0\)
\(\Rightarrow B_{Max}=\dfrac{0+2002}{-2003}=\dfrac{2002}{-2003}\)
Vậy giá trị lớn nhất của \(B\) là \(\dfrac{2002}{-2003}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm GTNN của biểu thức :
\(P\left(x\right)=\dfrac{2002x+2003\sqrt{1-x^2}+2004}{\sqrt{1-x^2}}\)
Tìm giá trị lớn nhất của A= \(\dfrac{2002}{\left|x\right|+2003}\)
\(\dfrac{2002}{\left|x\right|+2003}\) lớn nhất khi \(\left|x\right|+2003\) bé nhất
Mà \(\left|x\right|+2003\ge2003\Leftrightarrow x=0\)
Vậy \(A_{max}=\dfrac{2002}{2003}\Leftrightarrow x=0\)
Đúng 0
Bình luận (5)
Bài 1
\(a)A=\dfrac{\left|x\right|+2002}{2003}\)
\(b)B=\dfrac{-10}{\left|x\right|+16}\)
ak đề bài là tìm giá trị nhỏ nhất của các biểu thức
Đúng 0
Bình luận (0)
Tìm x:
a) \(\dfrac{\left(x+1\right)}{10}+\dfrac{\left(x+1\right)}{11}+\dfrac{\left(x+1\right)}{12}=\dfrac{x+1}{13}+\dfrac{x+1}{14}\)
b) \(\dfrac{x+4}{2000}+\dfrac{x+3}{2001}=\dfrac{x+2}{2002}+\dfrac{x+1}{2003}\)
a. \(\dfrac{\left(x+1\right)}{10}+\dfrac{\left(x+1\right)}{11}+\dfrac{\left(x+1\right)}{12}=\dfrac{x+1}{13}+\dfrac{x+1}{14}\)
\(\dfrac{x+1}{10}+\dfrac{x+1}{11}+\dfrac{x+1}{12}-\dfrac{x+1}{13}-\dfrac{x+1}{14}=0\)
\(\left(x+1\right)\left(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\right)=0\)
Vì \(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\ne0\)
\(\Rightarrow x+1=0\)
\(x=-1\)
b, \(\dfrac{x+4}{2000}+\dfrac{x+3}{2001}=\dfrac{x+2}{2002}+\dfrac{x+1}{2003}\\ \left(\dfrac{x+4}{2000}+1\right)+\left(\dfrac{x+3}{2001}+1\right)=\left(\dfrac{x+2}{2002}+1\right)+\left(\dfrac{x+1}{2003}+1\right)\\ \dfrac{x+2004}{2000}+\dfrac{x+2004}{2001}-\dfrac{x+2004}{2002}-\dfrac{x+2004}{2003}=0\\ x+2004\left(\dfrac{1}{2000}+\dfrac{1}{2001}-\dfrac{1}{2002}-\dfrac{1}{2003}\right)\)
vì \(\dfrac{1}{2000}+\dfrac{1}{2001}-\dfrac{1}{2002}-\dfrac{1}{2003}\ne0\\ \Rightarrow x+2004=0\\ x=-2004\)
Đúng 0
Bình luận (0)
a, \(\dfrac{x+1}{10}+\dfrac{x+1}{11}+\dfrac{x+1}{12}=\dfrac{x+1}{13}+\dfrac{x+1}{14}\)
\(\Rightarrow\dfrac{x+1}{10}+\dfrac{x+1}{11}+\dfrac{x+1}{12}-\dfrac{x+1}{13}-\dfrac{x+1}{14}=0\)
\(\Rightarrow\left(x+1\right)\left(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\right)=0\)
Vì \(10< 11< 12< 13< 14\) nên \(\dfrac{1}{10}>\dfrac{1}{11}>\dfrac{1}{12}>\dfrac{1}{13}>\dfrac{1}{14}\)
\(\Rightarrow\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}>0\)
\(\Rightarrow x+1=0\Rightarrow x=-1\)
Vậy.................
b, \(\dfrac{x+4}{2000}+\dfrac{x+3}{2001}=\dfrac{x+2}{2002}+\dfrac{x+1}{2003}\)
\(\Rightarrow\left(\dfrac{x+4}{2000}+1\right)+\left(\dfrac{x+3}{2001}+1\right)=\left(\dfrac{x+2}{2002}+1\right)+\left(\dfrac{x+1}{2003}+1\right)\)
\(\Rightarrow\dfrac{x+2004}{2000}+\dfrac{x+2004}{2001}=\dfrac{x+2004}{2002}+\dfrac{x+2004}{2003}\)
\(\Rightarrow\dfrac{x+2004}{2000}+\dfrac{x+2004}{2001}-\dfrac{x+2004}{2002}-\dfrac{x+2004}{2003}=0\)
\(\Rightarrow\left(x+2004\right)\left(\dfrac{1}{2000}+\dfrac{1}{2001}-\dfrac{1}{2002}-\dfrac{1}{2003}\right)=0\)
Vì \(2000< 2001< 2002< 2003\) nên \(\dfrac{1}{2000}>\dfrac{1}{2001}>\dfrac{1}{2002}>\dfrac{1}{2003}\)
\(\Rightarrow\dfrac{1}{2000}+\dfrac{1}{2001}-\dfrac{1}{2002}-\dfrac{1}{2003}>0\)
\(\Rightarrow x+2004=0\Rightarrow x=-2004\)
Vậy.................
Chúc bạn học tốt!!!
Đúng 0
Bình luận (0)
1.\(\left\{{}\begin{matrix}a,b>0\\2a+3b=4\end{matrix}\right.\)Tìm GTNN của
M=\(\dfrac{2002}{a}+\dfrac{2017}{b}+2096a-5501b\)
Bài này mình làm lâu rồi á bann sửa dấu `2a+3b<=4` thành `2a+3b=4` nhé!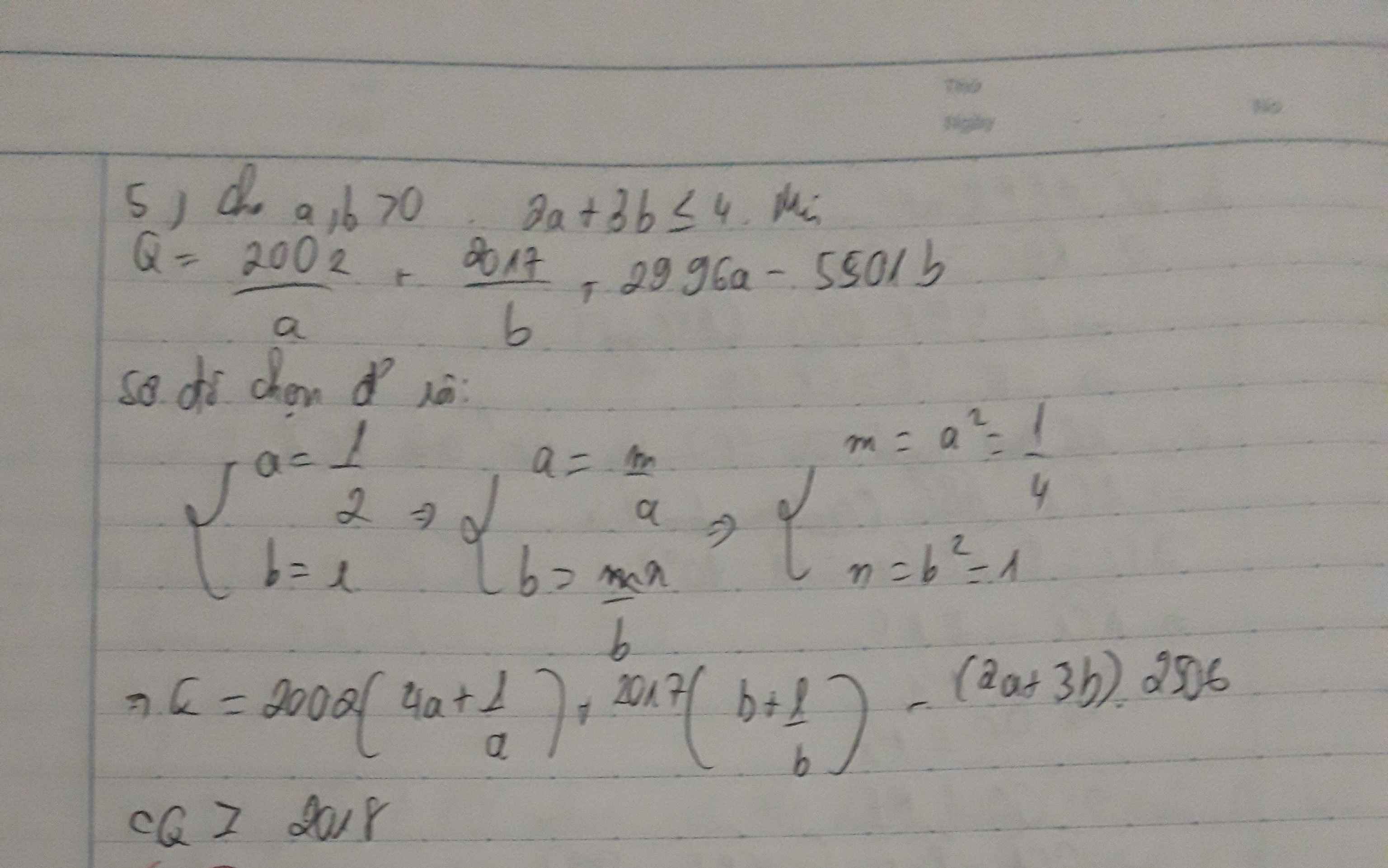
Đúng 0
Bình luận (1)
a. Tìm GTNN của các biểu thức sau
A=|x-2013|+|2014-x|
B=|x-123|+|x-456|
C=|x-1|+|x-2|+|x-3|
D=|x-1|+|x-2|+|x-3|+|x-4
b. Tìm GTLN của biểu thức
A=\(\frac{2003}{\left|x\right|+2004}\)
B=\(\frac{\left|x\right|+2003}{\left|x\right|+2002}\)
a)
\(A=\left|x-2013\right|+\left|2014-x\right|\)
Áp dụng bất đẳng thức \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta có:
\(A=\left|x-2013\right|+\left|2014-x\right|\ge\left|x-2013+2014-x\right|\)
\(\Rightarrow A\ge\left|1\right|\)
\(\Rightarrow A\ge1.\)
Dấu '' = '' xảy ra khi:
\(\left\{{}\begin{matrix}x-2013\ge0\\2014-x\le0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge2013\\x\le2014\end{matrix}\right.\Rightarrow2013\le x\le2014.\)
Vậy \(MIN_A=1\) khi \(2013\le x\le2014.\)
Chúc bạn học tốt!
Tính giá trị của các biểu thức sau 1) A1+2+2^2+...+2^{2015} 2) Bleft(dfrac{1}{4}-1right)cdotleft(dfrac{1}{9}-1right)cdotleft(dfrac{1}{16}-1right)cdotcdotcdotcdotcdotleft(dfrac{1}{400}-1right) 3) Cleft(dfrac{1}{4cdot9}+dfrac{1}{9cdot14}+dfrac{1}{14cdot19}+...+dfrac{1}{44cdot49}right)cdotdfrac{1-3-5-7-...-49}{89} 4) Ddfrac{2^{12}cdot3^5-4^6cdot9^2}{left(2^2cdot3right)^6+8^4cdot3^5}-dfrac{5^{10}cdot7^3-25^5cdot49^2}{left(125cdot7right)^3+5^9cdot14^3} 5) Edfrac{dfrac{1}{2003}+dfrac{1}{2004}-dfrac{1}...
Đọc tiếp
Tính giá trị của các biểu thức sau 1) \(A=1+2+2^2+...+2^{2015}\) 2) \(B=\left(\dfrac{1}{4}-1\right)\cdot\left(\dfrac{1}{9}-1\right)\cdot\left(\dfrac{1}{16}-1\right)\cdot\cdot\cdot\cdot\cdot\left(\dfrac{1}{400}-1\right)\) 3) \(C=\left(\dfrac{1}{4\cdot9}+\dfrac{1}{9\cdot14}+\dfrac{1}{14\cdot19}+...+\dfrac{1}{44\cdot49}\right)\cdot\dfrac{1-3-5-7-...-49}{89}\) 4) \(D=\dfrac{2^{12}\cdot3^5-4^6\cdot9^2}{\left(2^2\cdot3\right)^6+8^4\cdot3^5}-\dfrac{5^{10}\cdot7^3-25^5\cdot49^2}{\left(125\cdot7\right)^3+5^9\cdot14^3}\) 5) \(E=\dfrac{\dfrac{1}{2003}+\dfrac{1}{2004}-\dfrac{1}{2005}}{\dfrac{5}{2003}+\dfrac{5}{2004}-\dfrac{5}{2005}}-\dfrac{\dfrac{2}{2002}+\dfrac{2}{2003}-\dfrac{2}{2004}}{\dfrac{3}{2002}+\dfrac{3}{2003}-\dfrac{3}{2004}}\) 6) Cho 13+23+...+103=3025 Tính S= 23+43+63+...+203
MỌI NGƯỜI GIÚP EM VỚIBài 1: tìm xa)left|3x-5right|4b)dfrac{x+1}{10}+dfrac{x+1}{11}+dfrac{x+1}{12}dfrac{x+1}{13}+dfrac{x+1}{14}c)dfrac{x+4}{2000}+dfrac{x+3}{2001}dfrac{x+2}{2002}+dfrac{x+1}{2003}Bài 2: Tínha)dfrac{dfrac{1}{9}-dfrac{1}{7}-dfrac{1}{11}}{dfrac{4}{9}-dfrac{4}{7}-dfrac{4}{11}}+dfrac{dfrac{3}{5}-dfrac{3}{25}-dfrac{3}{125}-dfrac{3}{625}}{dfrac{4}{5}-dfrac{4}{25}-dfrac{4}{125}-dfrac{4}{625}}b)dfrac{1}{100.99}-dfrac{1}{99.98}-dfrac{1}{98.97}-...-dfrac{1}{3.2}-dfrac{1}{2.1}c)dfrac{left(dfr...
Đọc tiếp
MỌI NGƯỜI GIÚP EM VỚI
Bài 1: tìm x
a)\(\left|3x-5\right|=4\)
b)\(\dfrac{x+1}{10}+\dfrac{x+1}{11}+\dfrac{x+1}{12}=\dfrac{x+1}{13}+\dfrac{x+1}{14}\)
c)\(\dfrac{x+4}{2000}+\dfrac{x+3}{2001}=\dfrac{x+2}{2002}+\dfrac{x+1}{2003}\)
Bài 2: Tính
a)\(\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{\dfrac{4}{9}-\dfrac{4}{7}-\dfrac{4}{11}}+\dfrac{\dfrac{3}{5}-\dfrac{3}{25}-\dfrac{3}{125}-\dfrac{3}{625}}{\dfrac{4}{5}-\dfrac{4}{25}-\dfrac{4}{125}-\dfrac{4}{625}}\)
b)\(\dfrac{1}{100.99}-\dfrac{1}{99.98}-\dfrac{1}{98.97}-...-\dfrac{1}{3.2}-\dfrac{1}{2.1}\)
c)\(\dfrac{\left(\dfrac{3}{10}-\dfrac{4}{15}-\dfrac{7}{20}\right).\dfrac{5}{19}}{\left(\dfrac{1}{14}+\dfrac{1}{7}-\dfrac{-3}{35}\right).\dfrac{-4}{3}}\)
Bài 1:
a) \(\left|3x-5\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-5=4\\3x-5=-4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{3}\end{matrix}\right.\)
c) \(\dfrac{x+4}{2000}+\dfrac{x+3}{2001}=\dfrac{x+2}{2002}+\dfrac{x+1}{2003}\)
\(\Leftrightarrow\dfrac{x+2004}{2000}+\dfrac{x+2004}{2001}-\dfrac{x+2004}{2002}-\dfrac{x+2004}{2003}=0\)
\(\Leftrightarrow\left(x+2004\right)\left(\dfrac{1}{2000}+\dfrac{1}{2001}-\dfrac{1}{2002}-\dfrac{1}{2003}\right)=0\)
\(\Leftrightarrow x=-2004\)( do \(\dfrac{1}{2000}+\dfrac{1}{2001}-\dfrac{1}{2002}-\dfrac{1}{2003}\ne0\))
Bài 2:
a) \(=\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{4\left(\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}\right)}+\dfrac{3\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}{4\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}\)
\(=\dfrac{1}{4}+\dfrac{3}{4}=1\)
b) \(=-\left(\dfrac{1}{99.100}+\dfrac{1}{98.99}+\dfrac{1}{97.98}+...+\dfrac{1}{2.3}+\dfrac{1}{1.2}\right)\)
\(=-\left(\dfrac{1}{99}-\dfrac{1}{100}+\dfrac{1}{98}-\dfrac{1}{99}+...+1-\dfrac{1}{2}\right)\)
\(=-\left(1-\dfrac{1}{100}\right)=-\dfrac{99}{100}\)
Đúng 1
Bình luận (4)
Bài 1:
a) \(\left|3x-5\right|=4\) (1)
\(\Leftrightarrow\left[{}\begin{matrix}3x-5=4\\3x-5=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=9\\3x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{3}\end{matrix}\right.\)
b) \(\dfrac{x+1}{10}+\dfrac{x+1}{11}+\dfrac{x+1}{12}=\dfrac{x+1}{13}+\dfrac{x+1}{14}\)
\(\Leftrightarrow\left(x+1\right)\left(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\right)=0\)
\(\Leftrightarrow x+1=0\) \(\left(do\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\ne0\right)\)
\(\Leftrightarrow x=-1\)
c) \(\dfrac{x+4}{2000}+\dfrac{x+3}{2001}=\dfrac{x+2}{2002}+\dfrac{x+1}{2003}\)
\(\Leftrightarrow\left(\dfrac{x+4}{2000}+1\right)+\left(\dfrac{x+3}{2001}+1\right)=\left(\dfrac{x+2}{2002}+1\right)+\left(\dfrac{x+1}{2003}+1\right)\)
\(\Leftrightarrow\dfrac{x+2004}{2000}+\dfrac{x+2004}{2001}-\dfrac{x+2004}{2002}-\dfrac{x+2004}{2003}=0\)
\(\Leftrightarrow\left(x+2004\right)\left(\dfrac{1}{2000}+\dfrac{1}{2001}-\dfrac{1}{2002}-\dfrac{1}{2003}\right)=0\)
\(\Leftrightarrow x+2004=0\) \(\left(do\dfrac{1}{2000}+\dfrac{1}{2001}-\dfrac{1}{2002}-\dfrac{1}{2003}\ne0\right)\)
\(\Leftrightarrow x=-2004\)
Đúng 1
Bình luận (0)


























