Tìm x, y thỏa mãn |x-2|+ |y^20+9|=9
Bài 2: Căn thức bậc hai và hằng đẳng thức căn bậc hai của bình phương
Ta có: \(\left\{{}\begin{matrix}\left|x-2\right|\ge0;\forall x\\y^{20}\ge0;\forall y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|x-2\right|\ge0\\\left|y^{20}+9\right|\ge9\end{matrix}\right.\) ;\(\forall x;y\)
\(\Rightarrow\left|x-2\right|+\left|y^{20}+9\right|\ge9\) ;\(\forall x;y\)
Đăngt thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}\left|x-2\right|=0\\y^{20}=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho đường tròn tâm O có đ/kính AB. Trên cùng nửa mặt phẳng có bờ là đường thẳng AB, vẽ các tiếp tuyến Ax, By của đường tròn tâm O và một điểm c thuộc (O), (C khác A,B). Tiếp tuyến tại C của (O) cắt Ax và By lần lượt tại D,E. OE cắt (O) lần lượt tại V, K và cắt BC tại L
a. CM: LO. LE = LV. LK
b. CM: 1/VL-1/VE=2/KV
a: 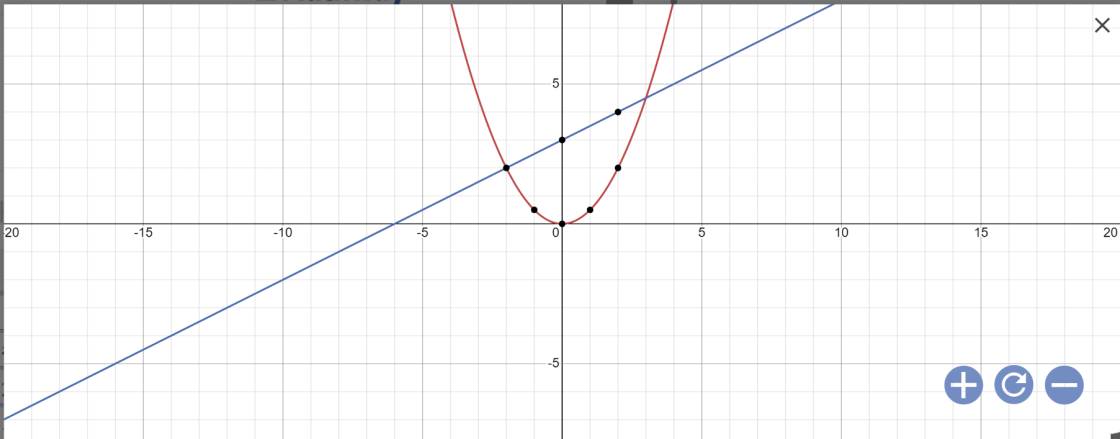
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=\dfrac{1}{2}x+3\)
=>\(x^2=x+6\)
=>\(x^2-x-6=0\)
=>(x-3)(x+2)=0
=>\(\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Thay x=3 vào (d), ta được:
\(y=\dfrac{1}{2}\cdot3+3=3+\dfrac{3}{2}=\dfrac{9}{2}\)
Thay x=-2 vào (d), ta được:
\(y=\dfrac{1}{2}\left(-2\right)+3=3-1=2\)
vậy: (d) cắt (P) tại \(A\left(3;\dfrac{9}{2}\right);B\left(-2;2\right)\)
Đúng 0
Bình luận (0)
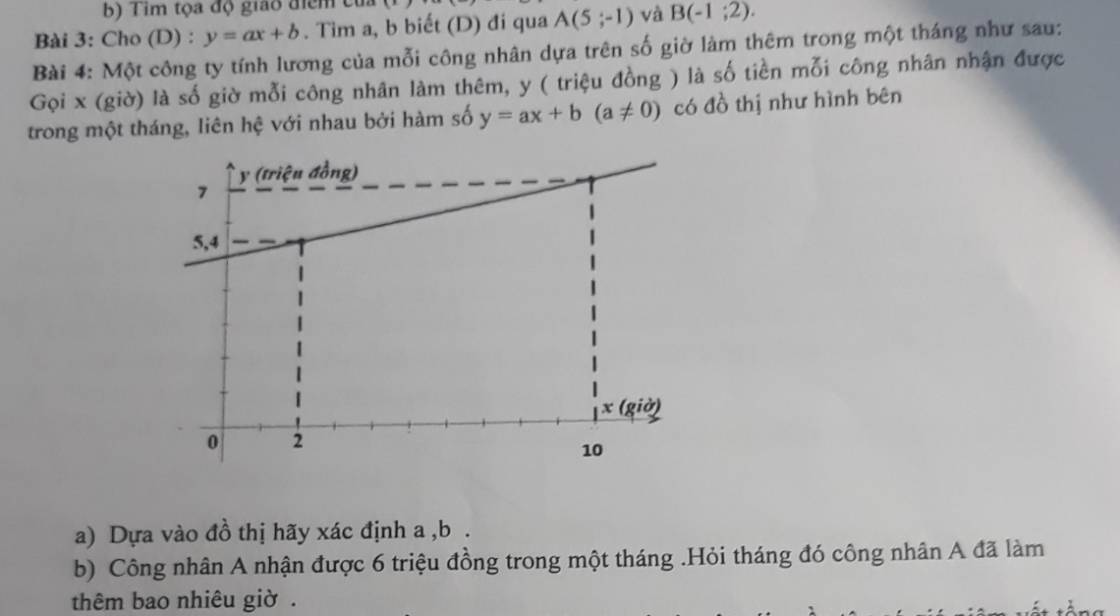
a: Số tiền cô Mai phải trả là:
\(50000\cdot4\cdot\left(1-15\%\right)=170000\left(đồng\right)\)
b: Số tiền chị Lan phải trả kể từ món hàng thứ 5 là:
348500-170000=178500(đồng)
Gọi số món hàng chị Lan đã mua là x(món)
(Điều kiện: \(x\in Z^+\))
Giá của 1 món hàng kể từ món hàng thứ 5 là:
\(50000\left(1-15\%\right)\cdot70\%=35000\cdot0,85=29750\left(đồng\right)\)
Số tiền phải trả cho x-4 món hàng là 29750(x-4)(đồng)
Do đó, ta có:
29750(x-4)=178500
=>x-4=6
=>x=10(nhận)
Vậy: Số hàng mà chị Lan đã mua là 10 món
Đúng 1
Bình luận (0)
Lời giải:
a. Lấy PT(1) x 2+ PT(2) x 3 ta được:
$2(-3x+y)+3(2x+7y)=(-9).2+3.52$
$\Leftrightarrow 23y=138$
$\Leftrightarrow y=6$
$x=\frac{-9-y}{-3}=\frac{-9-6}{-3}=5$
b.
$6x(x-1)=x+3$
$\Leftrightarrow 6x^2-7x-3=0$
$\Leftrightarrow (6x^2-9x)+(2x-3)=0$
$\Leftrightarrow 3x(2x-3)+(2x-3)=0$
$\Leftrightarrow (2x-3)(3x+1)=0$
$\Leftrightarrow 2x-3=0$ hoặc $3x+1=0$
$\Leftrightarrow x=\frac{3}{2}$ hoặc $x=\frac{-1}{3}$
Đúng 2
Bình luận (0)