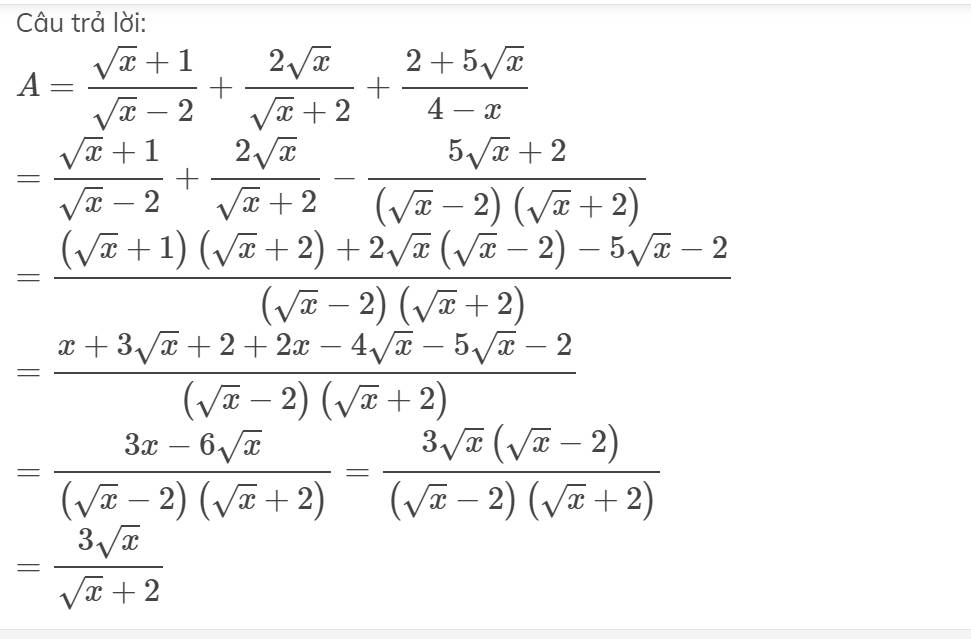Rút gọn biểu thức\(\dfrac{2+\sqrt x}{2-\sqrt x} - \dfrac{2-\sqrt x}{2+\sqrt x} -\dfrac{4}{x-4} \)

Những câu hỏi liên quan
1. Cho biểu thức: A=\(\left(\sqrt{x}+\dfrac{4\sqrt{x}}{\sqrt{x}-2}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}+\dfrac{4}{2\sqrt{x}-x}\right)\)
Rút gọn biểu thức trên
\(A=\left(\sqrt{x}+\dfrac{4\sqrt{x}}{\sqrt{x}-2}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}+\dfrac{4}{2\sqrt{x}-x}\right)\)ĐK : x > 0 ; x \(\ne\)4
\(=\left(\dfrac{x+2\sqrt{x}}{\sqrt{x}-2}\right):\left(\dfrac{x-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\right)=\dfrac{x\left(x-4\right)}{\left(\sqrt{x}-2\right)\left(x-4\right)}\)
\(=\dfrac{x}{\sqrt{x}-2}\)
Đúng 1
Bình luận (1)
Ta có: \(A=\left(\sqrt{x}+\dfrac{4\sqrt{x}}{\sqrt{x}-2}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}+\dfrac{4}{2\sqrt{x}-x}\right)\)
\(=\dfrac{x-2\sqrt{x}+4\sqrt{x}}{\sqrt{x}-2}:\dfrac{x-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x}{\sqrt{x}-2}\)
Đúng 0
Bình luận (0)
1.cho biểu thức A=\(\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{5}{x+\sqrt{x}-6}-\dfrac{1}{\sqrt{x}-2}\)với(x≥0;x≠4)
a)rút gọn A
b)tính A khi x=6+4\(\sqrt{2}\)
2.cho biểu thức P=\(\left(\dfrac{4\sqrt{x}}{\sqrt{x}+2}-\dfrac{8x}{x-4}\right):\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-2}+3\right)\)với x≥0;x≠1;x≠4
a)rút gọn P
b)tìm x để P=-4
Rút gọn biểu thức:
\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{2+5\sqrt{x}}{4-x}\)
\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{2+5\sqrt{x}}{4-x}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)+2\sqrt{x}\left(\sqrt{x}-2\right)-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
Đúng 1
Bình luận (2)
Ta có: \(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{5\sqrt{x}+2}{4-x}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
Đúng 0
Bình luận (1)
Cho biểu thức \(A=\dfrac{2}{2+\sqrt{x}}+\dfrac{2\sqrt{x}}{2-\sqrt{x}}-\dfrac{2x}{4-x}\) (x ≥ 0 ; x = 4)
Rút gọn biểu thức A
\(\dfrac{2\left(2-\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}+\dfrac{2\sqrt{x}\left(2+\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}-\dfrac{2x}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{4-2\sqrt{x}+4\sqrt{x}+2x-2x}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{4-2\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{2\left(2-\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{2}{2+\sqrt{x}}\)
Đúng 1
Bình luận (0)
\(\dfrac{2}{2+\sqrt{x}}\)+\(\dfrac{1}{2-\sqrt{x}}\)+\(\dfrac{2\sqrt{x}}{x-4}\)
rút gọn biểu thức
\(\dfrac{2}{2+\sqrt{x}}+\dfrac{1}{2-\sqrt{x}}+\dfrac{2\sqrt{x}}{x-4}\left(dkxd:x\ne4,x\ge0\right)\)
\(=\dfrac{2}{2+\sqrt{x}}+\dfrac{1}{2-\sqrt{x}}-\dfrac{2\sqrt{x}}{4-x}\)
\(=\dfrac{2}{2+\sqrt{x}}+\dfrac{1}{2-\sqrt{x}}-\dfrac{2\sqrt{x}}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\)
\(=\dfrac{2\left(2-\sqrt{x}\right)+2+\sqrt{x}-2\sqrt{x}}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\)
\(=\dfrac{4-2\sqrt{x}+2-\sqrt{x}}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\)
\(=\dfrac{6-3\sqrt{x}}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\)
\(=\dfrac{3\left(2-\sqrt{x}\right)}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\)
\(=\dfrac{3}{2+\sqrt{x}}\)
Đúng 4
Bình luận (1)
\(\dfrac{2}{2+\sqrt{x}}+\dfrac{1}{2-\sqrt{x}}+\dfrac{2\sqrt{x}}{x-4}\)
\(=\dfrac{2\left(2-\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}+\dfrac{2+\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}+\dfrac{2\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
\(=\dfrac{2\left(2-\sqrt{x}\right)+2+\sqrt{x}+2\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
\(=\dfrac{4-2\sqrt{x}+2+\sqrt{x}+2\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
\(=\dfrac{\sqrt{x}+6}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
Đúng 0
Bình luận (2)
1) Rút gọn biểu thức : A=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\) + \(\dfrac{2\sqrt{x}}{\sqrt{x}+2}\) + \(\dfrac{2+5\sqrt{x}}{4-x}\) với x≥0 ; x≠4
Cho biểu thức \(D=\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-\dfrac{\sqrt{x}}{\sqrt{x}+2}-\dfrac{5\sqrt{x}+5}{x-4}\right).\dfrac{x-4}{\sqrt{x}}\)
a. Tìm điều kiện để D được xác định
b. Rút gọn biểu thức
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne4\end{matrix}\right.\)
b: Ta có: \(D=\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-\dfrac{\sqrt{x}}{\sqrt{x}+2}-\dfrac{5\sqrt{x}+5}{x-4}\right)\cdot\dfrac{x-4}{\sqrt{x}}\)
\(=\dfrac{x+4\sqrt{x}+4-x+4\sqrt{x}-5\sqrt{x}-5}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{x-4}{\sqrt{x}}\)
\(=\dfrac{3\sqrt{x}-1}{\sqrt{x}}\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức
\(\left(\dfrac{\sqrt{x}}{x-4}+\dfrac{2}{2-\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right):\left(\sqrt{x}-2+\dfrac{10-x}{\sqrt{x}+2}\right)\)
\(\left(\dfrac{\sqrt{x}}{x-4}+\dfrac{2}{2-\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right):\left(\sqrt{x}-2+\dfrac{10-x}{\sqrt{x}+2}\right)\) (ĐK: x ≥ 0, x ≠ 4)
\(=\left[\dfrac{\sqrt{x}-2\left(\sqrt{x}+2\right)+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right]:\left[\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)+10-x}{\sqrt{x}+2}\right]\)
\(=\left(\dfrac{-6}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right):\dfrac{6}{\sqrt{x}+2}\)
\(=\dfrac{\left(-6\right)\left(\sqrt{x}+2\right)}{6\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{-1}{\sqrt{x}-2}\)
Vậy...
Đúng 2
Bình luận (0)
\(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{\sqrt{x}+4}{4-x}\)
rút gọn biểu thức. Mình cần gấp lắm rồi
đk : x >= 0, x khác 4
\(=\dfrac{x+2\sqrt{x}-\left(x-\sqrt{x}-2\right)-\sqrt{x}-4}{x-4}\)
\(=\dfrac{2\sqrt{x}-2}{x-4}=\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
Đúng 0
Bình luận (0)
1 a..Rút gọn biểu thức A = \(\dfrac{\text{ x 2 − 4 x + 4}}{\text{x 3 − 2 x 2 − ( 4 x − 8 ) }}\)
b. Rút gọn biểu thức B = \(\left(\dfrac{x+2}{\text{x }\sqrt{\text{x }}+1}-\dfrac{1}{\sqrt{\text{x}}+1}\right).\dfrac{\text{4 }\sqrt{x}}{3}\)
a.\(A=\dfrac{x^2-4x+4}{x^3-2x^2-\left(4x-8\right)}=\dfrac{\left(x-2\right)^2}{x^2\left(x-2\right)-4\left(x-2\right)}=\dfrac{\left(x-2\right)^2}{\left(x^2-4\right)\left(x-2\right)}=\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x+2}\)
Đúng 3
Bình luận (0)
\(A=\dfrac{\left(x-2\right)^2}{x^2\left(x-2\right)-4\left(x-2\right)}\left(x\ne\pm2\right)\\ A=\dfrac{\left(x-2\right)^2}{\left(x-2\right)^2\left(x+2\right)}=\dfrac{1}{x+2}\\ B=\dfrac{x+2-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\cdot\dfrac{4\sqrt{x}}{3}\left(x>0\right)\\ B=\dfrac{4\sqrt{x}\left(\sqrt{x}+1\right)}{3\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}=\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}\)
Đúng 2
Bình luận (0)