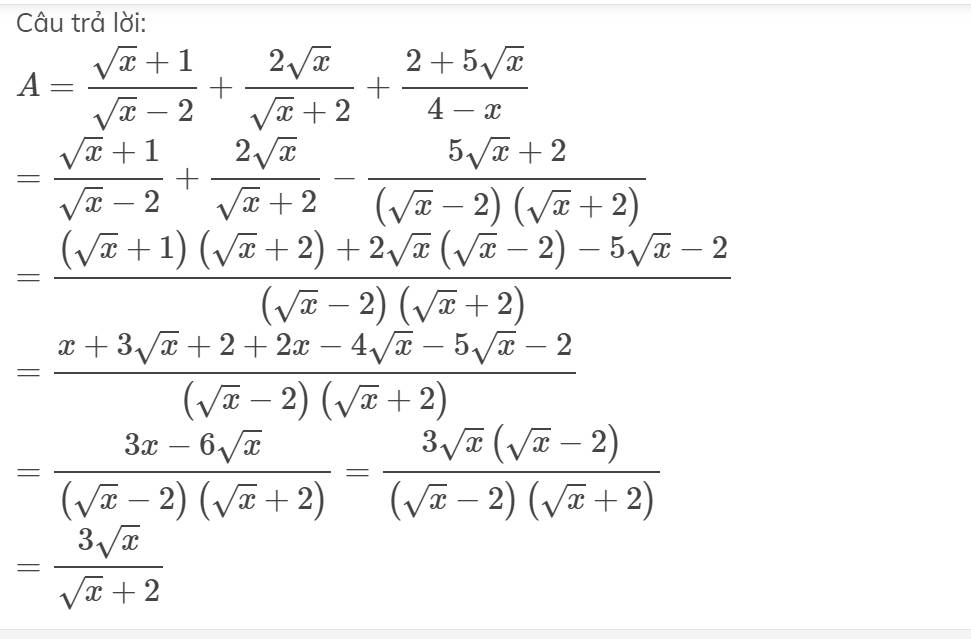18 tháng 12 2023 lúc 14:53
Các câu hỏi tương tự
6 tháng 8 2021 lúc 16:56
Rút gọn biểu thức dạng chữ:Qleft(dfrac{sqrt{x}+2}{x+2sqrt{x}+1}-dfrac{sqrt{x}-2}{x-1}right).left(x+sqrt{x}right) với x ≥0, x ≠1A Aleft(dfrac{1}{sqrt{x}-2}-dfrac{1}{sqrt{x}+2}+dfrac{4sqrt{x}}{4-x}right):dfrac{sqrt{x}+1}{x-4} với x ≥0, x ≠ 4Aleft(dfrac{sqrt{x}}{sqrt{x}+3}+dfrac{2sqrt{x}}{sqrt{x}-3}-dfrac{3x+9}{x-9}right):dfrac{1}{x+6sqrt{x}+9} với x ≥ 0, x ≠ 9Hộ vs ạ
Đọc tiếp
Rút gọn biểu thức dạng chữ:
Q=\(\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right).\left(x+\sqrt{x}\right)\) với x ≥0, x ≠1
A= \(A=\left(\dfrac{1}{\sqrt{x}-2}-\dfrac{1}{\sqrt{x}+2}+\dfrac{4\sqrt{x}}{4-x}\right):\dfrac{\sqrt{x}+1}{x-4}\) với x ≥0, x ≠ 4
\(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\right):\dfrac{1}{x+6\sqrt{x}+9}\) với x ≥ 0, x ≠ 9
Hộ vs ạ
Cho các biểu thức A = \(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{\sqrt{x}+2}{3-\sqrt{x}}+\dfrac{2\sqrt{x}-1}{x-5\sqrt{x}-6};B=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\) với x ≥ 0;x ≠ 4;x ≠ 9
a, Tính giá trị của biểu thức B khi x = 25
b, Rút gọn biểu thức A
c, Tìm các giá trị nguyên của x để A > B
22 tháng 5 2023 lúc 20:52
Rút gọn biểu thức A= (1-\(\dfrac{4}{x}\))(\(\dfrac{x-1}{x+3\sqrt{x}+2}\)-\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)) với x≥0 ; x≠4
Rút gọn biểu thức: A = \(\dfrac{10\sqrt{x}}{x+3\sqrt{x}-4}\) - \(\dfrac{2\sqrt{x}-3}{\sqrt{x}+4}\) + \(\dfrac{\sqrt{x}+1}{1-\sqrt{x}}\) ( Với x \(\ge\) 0, x \(\ne\) 1)
3 tháng 7 2023 lúc 21:57
34. Cho biểu thức A= \(\left(\dfrac{x+4\sqrt{x}+4}{x+\sqrt{x}-2}+\dfrac{x+\sqrt{x}}{1-x}\right):\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{1}{1-\sqrt{x}}\right)\)
a. Rút gọn A
c. Tính A với x thỏa mãn \(2x-3\sqrt{x}-5=0\)
rút gọn biểu thức \(P=\left(\dfrac{4\sqrt{x}}{2+\sqrt{x}}+\dfrac{8x}{4-x}\right):\left(\dfrac{\sqrt{x}-1}{x-2\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\) với x>0; x≠4; x≠9
Rút gọn biểu thức sau :
Bleft(dfrac{sqrt{x}}{sqrt{x}+4}+dfrac{4}{sqrt{x}-4}right):dfrac{x+16}{sqrt{x}+2} ( x ≥ 0 ; x ≠ 16 )
Pdfrac{x}{x-1}+dfrac{3}{x+1}-dfrac{6x-4}{x^2-1}
Adfrac{1}{x+sqrt{x}}+dfrac{2sqrt{x}}{x-1}-dfrac{1}{x-sqrt{x}}
Bleft(2-sqrt{3}right)sqrt{26+15sqrt{3}-left(2+sqrt{3}right)sqrt{26-15sqrt{3}}}
Aleft(sqrt{10}-sqrt{2}right)sqrt{3+sqrt{5}}
Đọc tiếp
Rút gọn biểu thức sau :
\(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}+4}+\dfrac{4}{\sqrt{x}-4}\right):\dfrac{x+16}{\sqrt{x}+2}\) ( x ≥ 0 ; x ≠ 16 )
\(P=\dfrac{x}{x-1}+\dfrac{3}{x+1}-\dfrac{6x-4}{x^2-1}\)
\(A=\dfrac{1}{x+\sqrt{x}}+\dfrac{2\sqrt{x}}{x-1}-\dfrac{1}{x-\sqrt{x}}\)
\(B=\left(2-\sqrt{3}\right)\sqrt{26+15\sqrt{3}-\left(2+\sqrt{3}\right)\sqrt{26-15\sqrt{3}}}\)
\(A=\left(\sqrt{10}-\sqrt{2}\right)\sqrt{3+\sqrt{5}}\)
Rút gọn biểu thức
a) A=\(2\sqrt{\left(2-\sqrt{5}\right)^2}-\dfrac{8}{3-\sqrt{5}}\)
b) B= \(\left(\dfrac{2\sqrt{x}}{x-4}-\dfrac{1}{\sqrt{x}+2}\right):\left(1+\dfrac{2}{\sqrt{x}-2}\right)\) Với x>0, x khác 4
cho biểu thức p=\(\left(\dfrac{4\sqrt{x}}{2+\sqrt{x}}+\dfrac{8x}{4-x}\right):\left(\dfrac{\sqrt{x}-1}{x-2\sqrt{x}}-\dfrac{1}{2\sqrt{x}}\right)\)với x>0;x khác 4,x khác 9 .rút gọn p