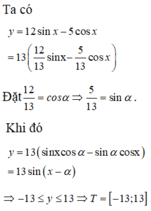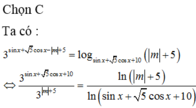tìm TGT : y=12sinx -5cosx

Những câu hỏi liên quan
Tìm tập giá trị T của hàm số y=12sinx-5cosx?
A. T=[-1;1]
B. T=[-7;7]
C. T=[-13;13]
D.T=[-17;17]
Tìm GTLN, GTNN của hàm số sau
a) y = 12sinx - 5cosx
b) y = 3cosx-4sinx+5
a) Ta có : -\(\sqrt{a^2+b^2}< =asinx+bcosx< =\sqrt{a^2+b^2}\)
=> \(-\sqrt{12^2+\left(-5\right)^2}< =y< =\sqrt{12^2+\left(-5\right)^2}\)
<=> \(-\sqrt{13}< =y< =\sqrt{13}\)
Vậy min=\(-\sqrt{13}\) ,max=\(\sqrt{13}\)
b) \(-\sqrt{9+16}< =3cosx-4sinx< =\sqrt{9+16}\)
<=> -5 <=3cos x -4sinx <= 5
<=> 0<= y <= 10
Vậy min=0 max=10
Đúng 0
Bình luận (0)
Tập xác định của hàm số \(\dfrac{1}{sinx-cosx}\)
Gía trị lớn nhất, giá trị nhỏ nhất của y= 12sinx - 5cosx
1/ \(y=\dfrac{1}{sinx-cosx}\)
Hàm số xác định khi
\(sinx-cosx\ne0\Rightarrow sinx\ne cosx\Rightarrow x\ne\dfrac{\pi}{4}+k\pi\)
2/
\(y=12sinx-5cosx=13\left(\dfrac{12}{13}sinx-\dfrac{5}{13}cosx\right)=13.sin\left(x-a\right)\)
Với góc a được xác định sao cho \(cosa=\dfrac{12}{13};sina=\dfrac{5}{13}\)
Do \(-1\le sin\left(x-a\right)\le1\Rightarrow-13\le13sin\left(x-a\right)\le13\)
\(\Rightarrow\left\{{}\begin{matrix}y_{min}=-13\\y_{max}=13\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm các giá trị m để phương trình
3
sin
x
+
5
cos
x
-
m
+
5
log
sin
x
+
5
cos
x...
Đọc tiếp
Tìm các giá trị m để phương trình 3 sin x + 5 cos x - m + 5 = log sin x + 5 cos x + 10 m + 5 có nghiệm
![]()
![]()
![]()
![]()
1. Tìm TXĐ, TGT của hàm số: y=\(\sqrt{x+2}+\sqrt{2-x}\)
`@` H/s xác định `<=>{(x+2 >= 0),(2-x >= 0):}<=>{(x >= -2),(x <= 2):}<=>-2 <= x <= 2`
`=>TXĐ: D=[-2;2]`
`@-2 <= x <= 2`
`<=>{(0 <= x+2 <= 4),(2 >= -x >= -2):}`
`<=>{(0 <= x+2 <= 4),(4 >= 2-x >= 0):}`
`<=>{(0 <= \sqrt{x+2} <= 2),(2 >= \sqrt{2-x} >= 0):}`
`=>TGT` là `[0;2]`
Đúng 3
Bình luận (0)
\(y=\sqrt{x+2}+\sqrt{2-x}\)
y có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x+2>0\\2-x>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>-2\\x>2\end{matrix}\right.\)
TXD D = \(\left(2;+\infty\right)\)
Đúng 0
Bình luận (1)
\(đk\left\{{}\begin{matrix}x+2\ge0\\2-x\ge0\end{matrix}\right.=>\left\{{}\begin{matrix}x\ge-2\\x\le2\end{matrix}\right.\)
\(=>TXĐ:\left[-2;2\right]\)
Đúng 2
Bình luận (1)
Tìm tất cả các giá trị thực của tham số m để phương trình
y
5
cos
x
−
m
sin
x
m
+
1
có nghiệm A.
m
≤
12
B.
m
≤
−
13
C.
m
≤
24
D.
m
≥
24
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình y = 5 cos x − m sin x = m + 1 có nghiệm
A. m ≤ 12
B. m ≤ − 13
C. m ≤ 24
D. m ≥ 24
Tìm TXD và TGT của hàm số
1. y=\(\dfrac{-x+5}{2x+3}\)
2. y=\(\dfrac{3x+2}{2x-1}\)
1: ĐKXĐ: \(x\ne-\dfrac{3}{2}\)
2: ĐKXĐ: \(x\ne\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Tìm số nghiệm của phương trình
sin
2
x
+
sin
x
-
1
2
sin
x
-
1
sin
2
x
2
c
o
t
2
x
trong khoảng ...
Đọc tiếp
Tìm số nghiệm của phương trình sin 2 x + sin x - 1 2 sin x - 1 sin 2 x = 2 c o t 2 x trong khoảng 0 ; π
A. 2
B. 3
C.4
D. 5
Tìm tất cả các tham số m để y = \(\sqrt{\dfrac{2sinx+5cosx-13}{2m.sinx+\left(m-1\right)cosx-m-2}}\) xác định với mọi R
\(2sinx+5cosx-13< 0;\forall x\)
\(\Rightarrow\) Hàm xác định trên R khi và chỉ khi:
\(2m.sinx+\left(2m-1\right)cosx-m< 0\) ;\(\forall x\)
\(\Leftrightarrow2m.sinx+\left(2m-1\right).cosx< m\); \(\forall x\)
\(\Rightarrow\dfrac{m}{\sqrt{\left(2m\right)^2+\left(2m-1\right)^2}}>1\)
\(\Rightarrow m\in\varnothing\)
Đúng 2
Bình luận (6)