Cho \(\Delta ABC\) , \(\widehat{B}-\widehat{C}\) = 900. Kẻ \(BD\perp AB\left(D\in AC\right),AH\perp BC\) tại H.
a) CMR: \(\widehat{HAB}=\widehat{ACB}=\widehat{DBC}\)
b) So sánh \(\widehat{ABH}=\widehat{CAH}\)
Những câu hỏi liên quan
Cho ΔABC vuông tại A (AB < AC)
Kẻ \(AH\perp BC\) tại H
a) Chứng minh \(\widehat{ABC}\) = \(\widehat{HAC}\)
b) Chứng minh \(\widehat{ACB}\) = \(\widehat{HAB}\)
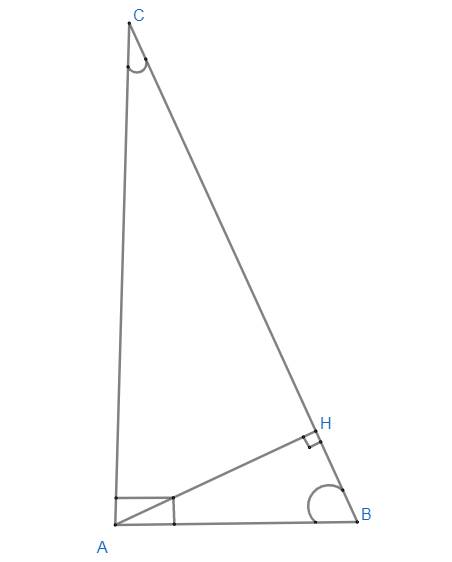
a)
Xét 2 tam giác vuông ABC và HAC có:
\(\widehat{C}\) chung
=> tg ABC \(\sim\) td HAC (g.g)
=> \(\widehat{ABC}=\widehat{HAC}\)
b)
Xét 2 tg vuông ACB và HAB có:
\(\widehat{B}\) chung
=> tg ACB \(\sim\) tg HAB (g.g)
=> \(\widehat{ACB}=\widehat{HAB}\)
Đúng 2
Bình luận (2)
Cho Delta ABCcó widehat{A}90^okẻ AHperp BCleft(Hin BCright),kẻ HDperp ABleft(Din ABright),kẻ HEperp HDleft(Ein ACright)a) C/m HD//AC,HEperp ACb) C/m widehat{BAH}widehat{ACH}c) Từ C kẻ đg thg perpvới tia pgiác của widehat{BAH}tại K. C/m CK là tia pgiác của widehat{ACB}
Đọc tiếp
Cho \(\Delta ABC\)có \(\widehat{A}=90^o\)kẻ \(AH\perp BC\left(H\in BC\right)\),kẻ \(HD\perp AB\left(D\in AB\right)\),kẻ \(HE\perp HD\left(E\in AC\right)\)
a) C/m \(HD//AC,HE\perp AC\)
b) C/m \(\widehat{BAH}=\widehat{ACH}\)
c) Từ C kẻ đg thg \(\perp\)với tia pgiác của \(\widehat{BAH}\)tại K. C/m CK là tia pgiác của \(\widehat{ACB}\)
Câu 1: Cho Delta ABC;widehat{A}100^0;widehat{B}40^0. Vẽ tia đối của AB là tia Ax. Vẽ tia AI là tia phân giác của widehat{xAC}
a) Chứng minh Ay // BC
b) Tính widehat{ACB}
Câu 2: Cho Delta ABC có widehat{A}90^0. Kẻ AHperp BCleft(Hin BCright). Kẻ HEperp ACleft(Ein ACright)
a) Chứng minh AB // HE
b) Biết widehat{B}60^0. Tính widehat{AHE};widehat{BAH}
Đọc tiếp
Câu 1: Cho \(\Delta ABC;\widehat{A}=100^0;\widehat{B}=40^0\). Vẽ tia đối của AB là tia Ax. Vẽ tia AI là tia phân giác của \(\widehat{xAC}\)
a) Chứng minh Ay // BC
b) Tính \(\widehat{ACB}\)
Câu 2: Cho \(\Delta ABC\) có \(\widehat{A}=90^0\). Kẻ \(AH\perp BC\left(H\in BC\right).\) Kẻ \(HE\perp AC\left(E\in AC\right)\)
a) Chứng minh AB // HE
b) Biết \(\widehat{B}=60^0.\) Tính \(\widehat{AHE};\widehat{BAH}\)
Câu 1
a.
Xét \(\Delta ABC\) có :
\(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^o\) ( định lý tổng 3 góc của 1 \(\Delta\) )
\(\Rightarrow\widehat{BCA}=40^o\) (1)
Ta có Ax là tia đối của AB
suy ra \(\widehat{BAC}+\widehat{CAx}=180^o\)
\(\widehat{CAx}=80^o\)
lại có Ay là tia phân giác \(\widehat{CAx}\)
\(\Rightarrow\widehat{xAy}=\widehat{yAc}=\dfrac{\widehat{CAx}}{2}=\dfrac{80^o}{2}=40^o\) (2)
Từ (1)(2) suy ra \(\widehat{yAc}=\widehat{ACB}=40^o\)
mà chúng ở vị trí so le trong
\(\Rightarrow\) Ay//BC
Bài 2
Rảnh làm sau , đến giờ học rồi .
Đúng 0
Bình luận (0)
cho \(\Delta ABC\left(\widehat{A}=90^o\right)\) , kẻ \(AH\perp BC\left(H\in BC\right)\) trên đường thẳng \(\perp BC\) tại B , lấy D khong cùng nửa mặt phẳng bờ BC đối với A
a) \(\Delta AHB=\Delta DBH\)
b) DB//DH
c) tính \(\widehat{ACB}\) biết \(\widehat{BAH}=35^o\)
a)
Xét tam giác AHB và tam giác DBH có:
AH = DB (gt)
AHB = DBH (= 900)
BH chung
=> Tam giác AHB = Tam giác DBH (c.g.c)
b)
DB _I_ BC (gt)
AH _I_ BC (gt)
=> DB // AH
c)
Tam giác HAB vuông tại H có:
HAB + HBA = 900
350 + HBA = 900
HBA = 900 - 350
HBA = 550
Tam giác ABC vuông tại A có:
ABC + ACB = 900
550 + ACB = 900
ACB = 900 - 550
ACB = 350
Đúng 0
Bình luận (0)
Cho △ ABC có \(\widehat{ABC}=45^o\) ; \(\widehat{ACB}=30^o\) . Kẻ AH ⊥ BC
a. Cmr : △ HAB vuông cân
b. Tính AB theo AH
c. Tính HC ; BC theo AH
d. Cmr : AB : BC : AC = \(\sqrt{2}:\left(1+\sqrt{3}\right):2\)
a: Xét ΔHAB vuông tại H có \(\widehat{ABH}=45^0\)
nên ΔHAB vuông cân tại H
b: \(AB=\sqrt{AH^2+HB^2}=AH\sqrt{2}\)
Đúng 0
Bình luận (0)
1.Cho Delta ABC vuông tại A có đường p/giác widehat{ABC} cắt AC tại E kẻ EHperp BC tại Hleft(Hin BCright)
C/m: a)Delta ABEDelta HBE
b)BE là trung trực AH
c)EC AE
2.Cho Delta ABC vuông tại A đường cao AH. Trên cạnh BC lấy D sao cho BDBA
a)C/m:widehat{BAD}widehat{BDA}
b)C/m:widehat{HAD}+widehat{BDA}widehat{DAC}+widehat{DAB}
Từ đó suy ra: AD là tia p/giác widehat{HAC}
c)Vẽ DKperp AC .C/m:AKAH...
Đọc tiếp
1.Cho \(\Delta ABC\) vuông tại A có đường p/giác \(\widehat{ABC}\) cắt AC tại E kẻ \(EH\perp BC\) tại H\(\left(H\in BC\right)\)
C/m: a)\(\Delta ABE=\Delta HBE\)
b)BE là trung trực AH
c)EC > AE
2.Cho \(\Delta ABC\) vuông tại A đường cao AH. Trên cạnh BC lấy D sao cho BD=BA
a)C/m:\(\widehat{BAD}=\widehat{BDA}\)
b)C/m:\(\widehat{HAD}+\widehat{BDA}=\widehat{DAC}+\widehat{DAB}\)
Từ đó suy ra: AD là tia p/giác \(\widehat{HAC}\)
c)Vẽ \(DK\perp AC\) .C/m:AK=AH
d)C/m:AB+AC < BC+AH
3.Cho \(\Delta ABC\) vuông tại A đường cao AH . Biết AH=4 cm; HB=2 cm; HC=8 cm
a)Tính AB; AC
b)C/m:\(\widehat{B}>\widehat{C}\)
Câu 1:
a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
góc ABE=góc HBE
Do đo: ΔABE=ΔHBE
b: Ta có:BA=BH
EA=EH
Do đó:BE là đường trung trực của AH
c: Ta có: EA=EH
mà EH<EC
nên EA<EC
Đúng 0
Bình luận (0)
Cho △ABC vuông tại A. Kẻ AH⊥BC. Trên BC lấy K sao cho BK= BA. Trên tia AC lấy I sao cho AI= AH. Chứng minh:
a) △ABC cân
b) \(\widehat{BAH}=\widehat{ACB};\widehat{HAK}=\widehat{KAI}\)
c) AC⊥KI
d) BC - AB > AC - AH
giúp với, cần gấp lắm, mai nộp òi
Đúng 0
Bình luận (3)
Cho ΔABC có AC > AB. Lấy điểm M à trung điểm của BC. Qua M kẻ đường thẳng d ⊥ BC, đường thẳng d cắt AC tại D.
a, CM: BD = DC
b, Kẻ AH ⊥ d tại H và cắt BC kéo dài tại I, CM: \(\widehat{CAH}=\widehat{DBC}\)
c, CM: ΔABC = ΔICB
d, Biết AB và CI cắt nhau tại N
CM: M, H, N thẳng hàng
Sửa đề: b: Cắt BD kéo dài tại I
a: Xét ΔDBC có
DM vừa là đường cao, vừa là trung tuyến
nên ΔDBC cân tại D
b: AH vuông góc với DM
DM vuông góc với BC
Do đó: AH//BC
=>góc DAI=góc DCB
=>góc CAH=góc DBC
c: Xét ΔDAI có góc DAI=góc DIA
nên ΔDAI cân tại D
=>DA=DI
=>AC=BI
Xét ΔABC và ΔICB có
AB=IC
BC chung
AC=IB
DO đó: ΔABC=ΔICB
Đúng 0
Bình luận (0)
Cho Delta ABCcân tại A, kẻ BDperp ACtại D, kẻ CEperp ABttext{ại}E, BD cắt CE tại Ia, Chứng minh: widehat{DBC}widehat{ECB}b, So sánh widehat{IBE}vtext{à}widehat{ICD}c, đường thẳng AI cắt Bc tại H. Chứng minh AIperp BCttext{ại}Hgiúp mik nhe các bn, nhaaaaaaa, cảm ơn trc nek
Đọc tiếp
Cho \(\Delta ABC\)cân tại A, kẻ \(BD\perp AC\)tại D, kẻ \(CE\perp ABt\text{ại}E\), BD cắt CE tại I
a, Chứng minh: \(\widehat{DBC}=\widehat{ECB}\)
b, So sánh \(\widehat{IBE}v\text{à}\widehat{ICD}\)
c, đường thẳng AI cắt Bc tại H. Chứng minh \(AI\perp BCt\text{ại}H\)
giúp mik nhe các bn, nhaaaaaaa, cảm ơn trc nek
pppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppp
Đúng 0
Bình luận (0)