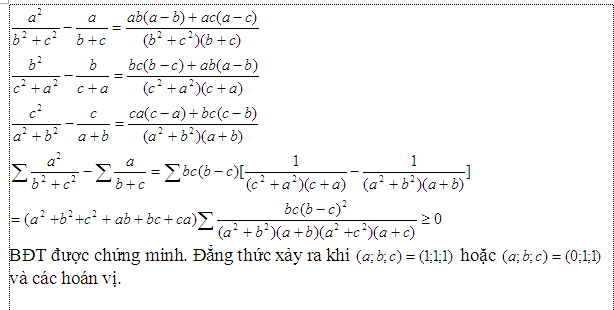Cho a+b+c=0. Tính \(A=\dfrac{a^2}{a^2-b^2-c^2}+\dfrac{b^2}{b^2-c^2-a^2}+\dfrac{c^2}{c^2-a^2-b^2}\)

Những câu hỏi liên quan
Cho a, b, c \(\ne0\) và a+b+c=0. Tính :
A= \(\dfrac{a^2}{a^2-b^2-c^2}+\dfrac{b^2}{b^2-c^2-a^2}+\dfrac{c^2}{c^2-a^2-b^2}\)
Ta có: \(a+b+c=0\Rightarrow a^2=\left(b+c\right)^2\Rightarrow a^2-2bc=b^2+c^2\)
\(\Rightarrow a^2-b^2-c^2=a^2-a^2+2bc=2bc\)
Tương tự: \(b^2-c^2-a^2=2ca;c^2-a^2-b^2=2ab\)
\(A=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ca}+\dfrac{c^2}{2ab}=\dfrac{a^3+b^3+c^3}{2abc}\)
Lại có: \(a+b+c=0\Rightarrow-a=b+c\)
\(\Rightarrow-a^3=b^3+c^3+3bc\left(b+c\right)\)
\(\Rightarrow a^3+b^3+c^3=-3bc\left(b+c\right)=3abc\left(b+c=-a\right)\)
=> \(A=\dfrac{3abc}{2abc}=\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
1)cho a,b,c 0. cmr:dfrac{1}{a^2+bc}+dfrac{1}{b^2+ca}+dfrac{1}{c^2+ab}ledfrac{a+b+c}{2abc}
2) cho a,b,c0 và a+b+c1. cmr:left(1+dfrac{1}{a}right)left(1+dfrac{1}{b}right)left(1+dfrac{1}{c}right)ge64
3) cho a,b,c0. cme:dfrac{a^2}{b^2}+dfrac{b^2}{c^2}+dfrac{c^2}{a^2}gedfrac{a}{b}+dfrac{b}{c}+dfrac{c}{a}
4) cho a,b,c0 .cmr:dfrac{a^3}{b^3}+dfrac{b^3}{c^3}+dfrac{c^3}{a^3}gedfrac{a^2}{b^2}+dfrac{b^2}{c^2}+dfrac{c^2}{a^2}
5)cho a,b,c0. cmr: dfrac{1}{aleft(a+bright)}+dfrac{1}{bleft(b+cright)}+dfrac{1}...
Đọc tiếp
1)cho a,b,c >0. \(cmr:\dfrac{1}{a^2+bc}+\dfrac{1}{b^2+ca}+\dfrac{1}{c^2+ab}\le\dfrac{a+b+c}{2abc}\)
2) cho a,b,c>0 và a+b+c=1. \(cmr:\left(1+\dfrac{1}{a}\right)\left(1+\dfrac{1}{b}\right)\left(1+\dfrac{1}{c}\right)\ge64\)
3) cho a,b,c>0. \(cme:\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\)
4) cho a,b,c>0 .\(cmr:\dfrac{a^3}{b^3}+\dfrac{b^3}{c^3}+\dfrac{c^3}{a^3}\ge\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\)
5)cho a,b,c>0. cmr: \(\dfrac{1}{a\left(a+b\right)}+\dfrac{1}{b\left(b+c\right)}+\dfrac{1}{c\left(c+a\right)}\ge\dfrac{27}{2\left(a+b+c\right)^2}\)
3/ Áp dụng bất đẳng thức AM-GM, ta có :
\(\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}\ge2\sqrt{\dfrac{\left(ab\right)^2}{\left(bc\right)^2}}=\dfrac{2a}{c}\)
\(\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge2\sqrt{\dfrac{\left(bc\right)^2}{\left(ac\right)^2}}=\dfrac{2b}{a}\)
\(\dfrac{c^2}{a^2}+\dfrac{a^2}{b^2}\ge2\sqrt{\dfrac{\left(ac\right)^2}{\left(ab\right)^2}}=\dfrac{2c}{b}\)
Cộng 3 vế của BĐT trên ta có :
\(2\left(\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\right)\ge2\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)\)
\(\Leftrightarrow\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\left(\text{đpcm}\right)\)
Đúng 0
Bình luận (1)
Bài 1:
Áp dụng BĐT AM-GM ta có:
\(\frac{1}{a^2+bc}+\frac{1}{b^2+ac}+\frac{1}{c^2+ab}\leq \frac{1}{2\sqrt{a^2.bc}}+\frac{1}{2\sqrt{b^2.ac}}+\frac{1}{2\sqrt{c^2.ab}}=\frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}{2abc}\)
Tiếp tục áp dụng BĐT AM-GM:
\(\sqrt{bc}+\sqrt{ac}+\sqrt{ab}\leq \frac{b+c}{2}+\frac{c+a}{2}+\frac{a+b}{2}=a+b+c\)
Do đó:
\(\frac{1}{a^2+bc}+\frac{1}{b^2+ac}+\frac{1}{c^2+ab}\leq \frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}{2abc}\leq \frac{a+b+c}{2abc}\) (đpcm)
Dấu "=" xảy ra khi $a=b=c$
Đúng 1
Bình luận (0)
Bài 2:
Thay $1=a+b+c$ và áp dụng BĐT AM-GM ta có:
\(\left(1+\frac{1}{a}\right)\left(1+\frac{1}{b}\right)\left(1+\frac{1}{c}\right)=\frac{(a+1)(b+1)(c+1)}{abc}\)
\(=\frac{(a+a+b+c)(b+a+b+c)(c+a+b+c)}{abc}\)
\(\geq \frac{4\sqrt[4]{a.a.b.c}.4\sqrt[4]{b.a.b.c}.4\sqrt[4]{c.a.b.c}}{abc}=\frac{64abc}{abc}=64\)
Ta có đpcm
Dấu "=" xảy ra khi $a=b=c=\frac{1}{3}$
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
cho a+b+c=0 và abc≠0 tính giá trị biểu thức
\(P=\dfrac{1}{b^2+c^2-a^2}+\dfrac{1}{a^2+c^2-b^2}+\dfrac{1}{a^2+b^2-c^2}\)
Xét b2+c2-a2=(b+c)2-a2-2bc=(a+b+c)(b+c-a)-2bc=-2bc
cmtt=>P=\(\dfrac{1}{-2bc}\)+\(\dfrac{1}{-2ab}\)+\(\dfrac{1}{-2ac}\)=\(\dfrac{a+b+c}{-2abc}\)=0
Đúng 0
Bình luận (0)
Cho a,b,c đôi một khác nhau và a+b+c=0. Tính
P= \(\dfrac{ab^{2}}{a^{2}+b^{2}-c^{2}}\)+\(\dfrac{bc^{2}}{b^{2}+c^{2}-a^{2}}\)+\(\dfrac{ca^{2}}{c^{2}+a^{2}-b^{2}}\)
Ta có: a+b+c=0
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=-c\\b+c=-a\\a+c=-b\end{matrix}\right.\)
Ta có: \(P=\dfrac{ab^2}{a^2+b^2-c^2}+\dfrac{bc^2}{b^2+c^2-a^2}+\dfrac{ca^2}{c^2+a^2-b^2}\)
\(=\dfrac{ab^2}{\left(a+b\right)^2-c^2-2ab}+\dfrac{bc^2}{\left(b+c\right)^2-a^2-2bc}+\dfrac{ca^2}{\left(c+a\right)^2-b^2-2ac}\)
\(=\dfrac{ab^2}{\left(a+b+c\right)\left(a+b-c\right)-2ab}+\dfrac{bc^2}{\left(b+c+a\right)\left(b+c-a\right)-2bc}+\dfrac{ca^2}{\left(c+a+b\right)\left(c+a-b\right)-2ac}\)
\(=\dfrac{ab^2}{-2ab}+\dfrac{bc^2}{-2bc}+\dfrac{ca^2}{-2ac}\)
\(=\dfrac{-ab\cdot b}{2ab}+\dfrac{-bc^2}{2bc}+\dfrac{-ca^2}{2ac}\)
\(=\dfrac{-b}{2}+\dfrac{-c}{2}+\dfrac{-a}{2}=\dfrac{-\left(a+b+c\right)}{2}=\dfrac{0}{2}=0\)
Đúng 2
Bình luận (0)
1. Cho a,b,c không đồng thời bằng 0 và a+b+c=0. Rút gọn:
\(N=\dfrac{a^2}{a^2-b^2-c^2}+\dfrac{b^2}{b^2-c^2-a^2}+\dfrac{c^2}{c^2-a^2-b^2}\)
2. CMR: Nếu a+b+c=2x thì:
\(\dfrac{1}{x-a}+\dfrac{1}{x-b}+\dfrac{1}{x-c}-\dfrac{1}{x}=\dfrac{abc}{x\left(x-a\right)\left(x-b\right)\left(x-c\right)}\)
\(1,a+b+c=0\Leftrightarrow a=-b-c\Leftrightarrow a^2=b^2+2bc+c^2\Leftrightarrow b^2+c^2=a^2-2bc\)
Tương tự: \(\left\{{}\begin{matrix}a^2+b^2=c^2-2ab\\c^2+a^2=b^2-2ac\end{matrix}\right.\)
\(\Leftrightarrow N=\dfrac{a^2}{a^2-a^2+2bc}+\dfrac{b^2}{b^2-b^2+2ca}+\dfrac{c^2}{c^2-c^2+2ac}\\ \Leftrightarrow N=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2bc}=\dfrac{a^3+b^3+c^3}{2abc}=\dfrac{a^3+b^3+c^3-3abc+3abc}{2abc}\\ \Leftrightarrow N=\dfrac{\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)+3abc}{2abc}\\ \Leftrightarrow N=\dfrac{3abc}{2abc}=\dfrac{3}{2}\)
Đúng 2
Bình luận (0)
Cho a, b, c > 0. Chứng minh \(\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\)
Hình như thế này mới đúng chứ \(\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge\dfrac{b}{a}+\dfrac{c}{b}+\dfrac{a}{c}\)
Áp dụng BĐT Cosi:
\(\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}\ge2.\dfrac{a}{c};\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge2.\dfrac{b}{a};\dfrac{c^2}{a^2}+\dfrac{a^2}{b^2}\ge2.\dfrac{c}{b}\)
\(\Rightarrow2\left(\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\right)\ge2\left(\dfrac{b}{a}+\dfrac{c}{b}+\dfrac{a}{c}\right)\)
\(\Leftrightarrow\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge\dfrac{b}{a}+\dfrac{c}{b}+\dfrac{a}{c}\)
Đẳng thức xảy ra khi \(a=b=c>0\)
Đúng 2
Bình luận (0)
cho \(\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}=0\) và \(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\), tính A \(=\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}\)
Từ giả thiết : \(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\)
\(\Rightarrow\left(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}\right)^2=1\)
\(\Rightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2.\left(\dfrac{xy}{ab}+\dfrac{yz}{bc}+\dfrac{zx}{ca}\right)=1\)
\(\Rightarrow A+2.\left(\dfrac{xyc+yza+xzb}{abc}\right)=1\left(1\right)\)
Mà theo gt : \(\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}=0\)
\(\Rightarrow\dfrac{ayz+bxz+cxy}{xyz}=0\)
\(\Rightarrow ayz+bzx+cxy=0\)
Do đó : \(\left(1\right)=A=1\)
Đúng 1
Bình luận (0)
Cho a+b+c=0 và abc khác 0,tính giá trị của biểu thức:
P= \(\dfrac{1}{b^2+c^2-a^2}+\dfrac{1}{a^2+c^2-b^2}+\dfrac{1}{a^2+b^2-c^2}\)
P= \(\dfrac{1}{b^2+c^2-a^2}+\dfrac{1}{a^2+c^2-b^2}+\dfrac{1}{a^2+b^2-c^2}\)
=
\(\dfrac{a+b+c}{\left(b^2+c^2-a^2\right)\left(a+b+c\right)}+\dfrac{a+b+c}{\left(a^2+c^2-b^2\right)\left(a+b+c\right)}+\dfrac{a+b+c}{\left(a^2+b^2-c^2\right)\left(a+b+c\right)}\)
= 0+0+0 = 0
Vậy P= 0
Ngu vãi ko bt đúng không nx
\(P=\dfrac{1}{b^2+c^2-a^2}+\dfrac{1}{a^2+c^2-b^2}+\dfrac{1}{a^2+b^2-c^2}\)
\(=\dfrac{1}{b^2+c^2-\left(-b-c\right)^2}+\dfrac{1}{a^2+c^2-\left(-c-a\right)^2}+\dfrac{1}{a^2+b^2-\left(-a-b\right)^2}\)
\(=\dfrac{1}{b^2+c^2-\left(b+c\right)^2}+\dfrac{1}{a^2+c^2-\left(c+a\right)^2}+\dfrac{1}{a^2+b^2-\left(a+b\right)^2}\)
\(=\dfrac{1}{b^2+c^2-b^2-2bc-c^2}+\dfrac{1}{a^2+c^2-a^2-2ac-c^2}+\dfrac{1}{a^2+b^2-a^2-2ab-b^2}\)
\(=\dfrac{1}{-2bc}+\dfrac{1}{-2ac}+\dfrac{1}{-2ab}\)
\(=\dfrac{a}{-2bca}+\dfrac{b}{-2acb}+\dfrac{c}{-2abc}\)
\(=\dfrac{a+b+c}{-2abc}=\dfrac{0}{-2abc}=0\)
Đúng 1
Bình luận (1)
Cho a,b,c >0. CMR: \(\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\ge\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\)
cho \(a+b+c=0\) cmr : \(A=\dfrac{a^2}{a^2-b^2-c^2}+\dfrac{b^2}{b^2-c^2-a^2}+\dfrac{c^2}{c^2-a^2-b^2}=\dfrac{3}{2}\)
\(Từ:gt\) \(a+b+c=0\)
\(\Rightarrow b+c=-a\Rightarrow b^2+2bc+c^2=a^2\Rightarrow a^2-b^2-c^2=2bc\)
cmt tương tự với :
\(b^2-a^2-c^2=2ac\)
\(c^2-a^2-b^2=2ab\)
\(\Rightarrow A=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}\)
\(\Rightarrow A=\dfrac{a^3}{2abc}+\dfrac{b^3}{2abc}+\dfrac{c^3}{2abc}\)
\(\Rightarrow A=\dfrac{1}{2abc}\left(a^3+b^3+c^3\right)\)
\(\Rightarrow A=\dfrac{3abc}{2abc}\)
\(\Rightarrow A=\dfrac{3}{2}\)
Đúng 1
Bình luận (0)