Mn giúp em bài 28 và bài 31 với ạ

Những câu hỏi liên quan
Mn giúp em bài 28 và bài 31 với ạ
Mn giúp e bài 28 vs ạ . Em thanks trước
Xem chi tiết
bài 28 ý hả bn! bn nêu đề ra nha!
mk dùng sách vnen nên ko có mấy cái đó.
Đúng 0
Bình luận (0)
Mn giúp mình với ạ!Mình cảm ơn!!!
Bài 1:Chứng minh rằng B = 2 + 22 + 23 + 24 + ........ + 299 + 2100 chia hết cho 31.
Mình cảm ơn mn ạ!Giúp mình với tối nay 20:00 mình phải nộp bài rồi!!!
![]()
\(B=2+2^2+2^3+2^4+...+2^{99}+2^{100}=2\left(1+2^2+2^3+2^4\right)+...+2^{96}\left(1+2^2+2^3+2^4\right)=2.31+2^6.31+...+2^{96}.31=31\left(2+2^6+...+2^{96}\right)⋮31\)
Đúng 5
Bình luận (1)
B=2+22+23+24+...+299+2100=2(1+22+23+24)+...+296(1+22+23+24)=2.31+26.31+...+296.31=31(2+26+...+296)⋮31
Đúng 1
Bình luận (0)
Mn ơi giúp em làm bài 3 và bài 4 với ạ,mai đi học rồi mà em ko bt Làm:((
3)
a)vì góc E=F=40 mà 2 góc có vị trí đồng vị
b)vì góc F=M=40 mà 2 góc có vị trí so le ngoài
b//c mà b//a suy ra a//c
Đúng 0
Bình luận (0)
4)
a)vì góc A1=B1 mà 2 góc có vị trí đồng vị
b)B4=B1, A3=A1
vì B1+B2=180 suy ra B2=110=B3 đối đỉnh
A2=A4=110
Đúng 0
Bình luận (0)
Bài 3: (gọi tạm hai góc có trong hình là E1 và F1)
a/ Ta có: \(\hat{E_1}=\hat{F_1}=40\text{°}\)
- Hai góc ở vị trí đồng vị. Vậy:\(a\text{ // }b\)
-------------------
b/ Gọi góc đối đỉnh F1 là F2
- \(F_1=F_2=40\text{°}\) (đối đỉnh)
- \(F_2=M_1=40\text{°}\). Mà F2 và M1 là hai góc đồng vị
⇒\(b\text{ // }c\)
- \(a\text{ // }b\); \(b\text{ // }c\)
Vậy: \(a\text{ // }c\)
==========
Bài 4:
a/ \(A_1=B_1=70\text{°}\text{ }\)
- Mà A1 và B1 là hai góc đồng vị. Vậy: \(a\text{ // }b\)
--------------------
b/ \(\hat{A_2}=180\text{}\text{°}-\hat{A_1}=130\text{°}\) (kề bù)
\(\hat{A_3}=\hat{A_1}=70\text{°}\)(đối đỉnh)
\(\hat{A_4}=\hat{A_2}=130\text{°}\) (đối đỉnh)
\(\hat{B_2}=180\text{°}-\hat{A_1}=130\text{°}\) (trong cùng phía)
\(\hat{B_3}=\hat{B_2}=130\text{°}\) (đối đỉnh)
\(\hat{B_4}=\hat{A_1}=70\text{°}\) (so le trong)
Chúc bạn học tốt
Đúng 0
Bình luận (0)
Chỉ giúp em với ạ bài 31
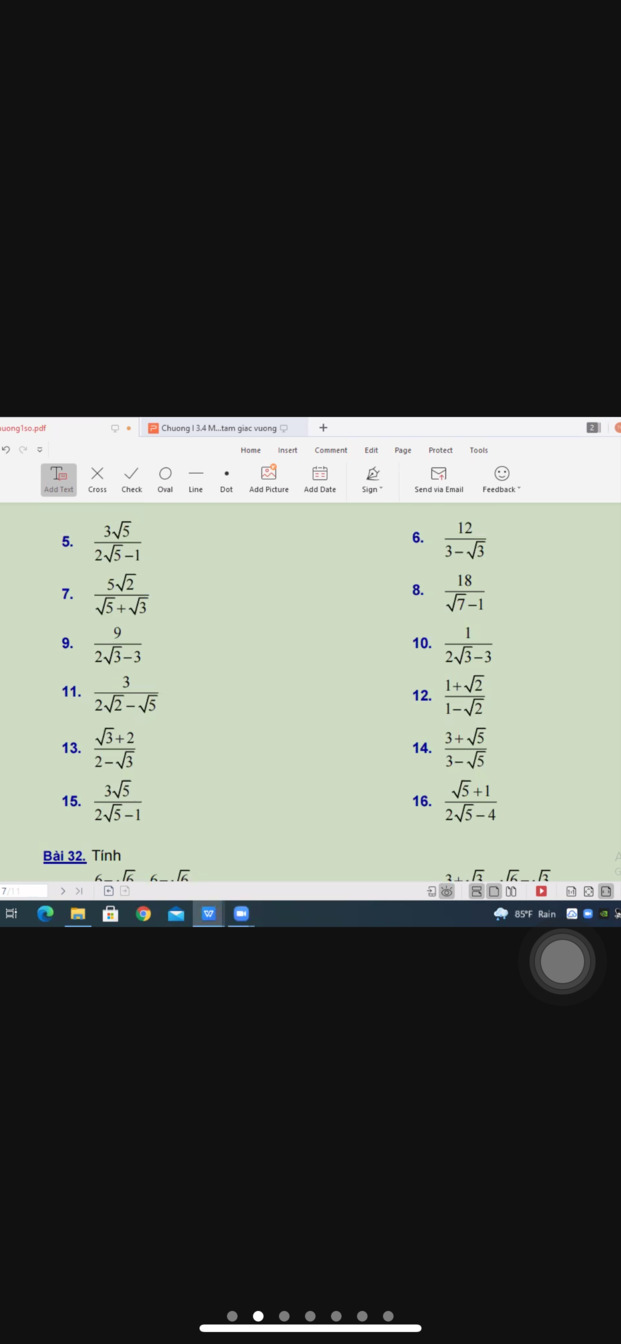
1. \(\dfrac{2}{2-\sqrt{3}}=\dfrac{2\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{4+2\sqrt{3}}{2^2-\left(\sqrt{3}\right)^2}=\dfrac{4+2\sqrt{3}}{4-3}=4+2\sqrt{3}\)
2. \(\dfrac{1}{\sqrt{3}+\sqrt{2}}=\dfrac{\sqrt{3}-\sqrt{2}}{\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)}=\dfrac{\sqrt{3}-\sqrt{2}}{\left(\sqrt{3}\right)^2-\left(\sqrt{2}\right)^2}=\dfrac{\sqrt{3}-\sqrt{2}}{3-2}\)
\(=\sqrt{3}-\sqrt{2}\)
3. \(\dfrac{1}{\sqrt{5}+\sqrt{7}}=\dfrac{\sqrt{7}-\sqrt{5}}{\left(\sqrt{5}+\sqrt{7}\right)\left(\sqrt{7}-\sqrt{5}\right)}=\dfrac{\sqrt{7}-\sqrt{5}}{\left(\sqrt{7}\right)^2-\left(\sqrt{5}\right)^2}=\dfrac{\sqrt{7}-\sqrt{5}}{7-5}\)
\(=\dfrac{\sqrt{7}-\sqrt{5}}{2}\)
4. \(\dfrac{1}{5-2\sqrt{6}}=\dfrac{5+2\sqrt{6}}{\left(5-2\sqrt{6}\right)\left(5+2\sqrt{6}\right)}=\dfrac{5+2\sqrt{6}}{5^2-\left(2\sqrt{6}\right)^2}=\dfrac{5+2\sqrt{6}}{25-24}\)
\(=5+2\sqrt{6}\)
5. \(\dfrac{3\sqrt{5}}{2\sqrt{5}-1}=\dfrac{3\sqrt{5}\left(2\sqrt{5}+1\right)}{\left(2\sqrt{5}-1\right)\left(2\sqrt{5}\right)+1}=\dfrac{30+3\sqrt{5}}{\left(2\sqrt{5}\right)^2-1^2}=\dfrac{30+3\sqrt{5}}{20-1}\)
\(=\dfrac{30+3\sqrt{5}}{19}\)
6. \(\dfrac{12}{3-\sqrt{3}}=\dfrac{12}{\sqrt{3}\left(\sqrt{3}-1\right)}=\dfrac{4\sqrt{3}}{\sqrt{3}-1}=\dfrac{4\sqrt{3}\left(\sqrt{3}+1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
\(\dfrac{12+4\sqrt{3}}{\left(\sqrt{3}\right)^2-1^2}=\dfrac{2\left(6+2\sqrt{3}\right)}{3-1}=6+2\sqrt{3}\)
7. \(\dfrac{5\sqrt{2}}{\sqrt{5}+\sqrt{3}}=\dfrac{5\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}=\dfrac{5\sqrt{10}-5\sqrt{6}}{\left(\sqrt{5}\right)^2-\left(\sqrt{3}\right)^2}\)
\(=\dfrac{5\sqrt{10}-5\sqrt{6}}{5-3}=\dfrac{5\sqrt{10}-5\sqrt{6}}{2}\)
8. \(\dfrac{18}{\sqrt{7}-1}=\dfrac{18\left(\sqrt{7}+1\right)}{\left(\sqrt{7}-1\right)\left(\sqrt{7}+1\right)}=\dfrac{18\left(\sqrt{7}+1\right)}{\left(\sqrt{7}\right)^2-1^2}=\dfrac{18\left(\sqrt{7}+1\right)}{7-1}\)
\(=3\left(\sqrt{7}+1\right)=3\sqrt{7}+3\)
9. \(\dfrac{9}{2\sqrt{3}-3}=\dfrac{9\left(2\sqrt{3}+3\right)}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}=\dfrac{9\left(2\sqrt{3}+3\right)}{\left(2\sqrt{3}\right)^2-3^2}=\dfrac{9\left(2\sqrt{3}+3\right)}{12-9}\)
\(3\left(2\sqrt{3}+3\right)=6\sqrt{3}+9\)
10. \(\dfrac{1}{2\sqrt{3}-3}=\dfrac{2\sqrt{3}+3}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}=\dfrac{2\sqrt{3}+3}{\left(2\sqrt{3}\right)^2-3^2}=\dfrac{2\sqrt{3}+3}{12-9}\)
\(=\dfrac{2\sqrt{3}+3}{3}\)
11. \(\dfrac{3}{2\sqrt{2}-\sqrt{5}}=\dfrac{3\left(2\sqrt{2}+\sqrt{5}\right)}{\left(2\sqrt{2}-\sqrt{5}\right)\left(2\sqrt{2}+\sqrt{5}\right)}=\dfrac{3\left(2\sqrt{2}+\sqrt{5}\right)}{\left(2\sqrt{2}\right)^2-\left(\sqrt{5}\right)^2}\)
\(=\dfrac{3\left(2\sqrt{2}+\sqrt{5}\right)}{8-5}=2\sqrt{2}+5\)
12. \(\dfrac{1+\sqrt{2}}{1-\sqrt{2}}=\dfrac{\left(1+\sqrt{2}\right)\left(1+\sqrt{2}\right)}{\left(1-\sqrt{2}\right)\left(1+\sqrt{2}\right)}=\dfrac{\left(1+\sqrt{2}\right)^2}{1^2-\left(\sqrt{2}\right)^2}=\dfrac{3+2\sqrt{2}}{-1}\)
\(=-3-2\sqrt{2}\)
13. \(\dfrac{\sqrt{3}+2}{2-\sqrt{3}}=\dfrac{\left(\sqrt{3}+2\right)\left(\sqrt{3}+2\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{\left(\sqrt{3}+2\right)^2}{2^2-\left(\sqrt{3}\right)^2}=\dfrac{7+4\sqrt{3}}{4-3}=7+4\sqrt{3}\)
14. \(\dfrac{3+\sqrt{5}}{3-\sqrt{5}}=\dfrac{\left(3+\sqrt{5}\right)\left(3+\sqrt{5}\right)}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}=\dfrac{\left(3+\sqrt{5}\right)^2}{3^2-\left(\sqrt{5}\right)^2}=\dfrac{14+6\sqrt{5}}{9-5}\)
\(=\dfrac{7+3\sqrt{5}}{2}\)
15. giống câu 5
16. \(\dfrac{\sqrt{5}+1}{2\sqrt{5}-4}=\dfrac{\left(\sqrt{5}+1\right)\left(2\sqrt{5}+4\right)}{\left(2\sqrt{5}-4\right)\left(2\sqrt{5}+4\right)}=\dfrac{14+6\sqrt{5}}{\left(2\sqrt{5}\right)^2-4^2}=\dfrac{14+6\sqrt{5}}{4}\)
\(=\dfrac{7+3\sqrt{5}}{2}\)
Đúng 1
Bình luận (0)
- Sử dụng liên hợp thôi nha mình làm tham khảo câu 1, 4 các câu khác tương tự .
\(1,\dfrac{2}{2-\sqrt{3}}=\dfrac{2\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{4+2\sqrt{3}}{4-3}=3+2\sqrt{3}+1=\left(\sqrt{3}+1\right)^2\)
\(4,\dfrac{1}{5-2\sqrt{6}}=\dfrac{5+2\sqrt{6}}{5^2-\left(2\sqrt{6}\right)^2}=5+2\sqrt{6}\)
Đúng 0
Bình luận (0)
(Em không biết cách làm bài này ạ. Mn giúp em với ạ!!!) Có 28 phần thưởng gồm 9 cuốn sách (giống nhau), 8 cuốn số (giống nhau), và 11 chiếc bút (giống nhau) được phát cho 14 học sinh giỏi, mỗi người nhận được 2 phần thưởng khác loại. An và Bình là hai trong số 14 học sinh được nhận thưởng. Hỏi có bao nhiêu cách phát phần thưởng cho 14 học sinh đó để An và Bình được nhận phần thưởng có loại giống nhau?Đáp án: 51744
Đọc tiếp
(Em không biết cách làm bài này ạ. Mn giúp em với ạ!!!)
Có 28 phần thưởng gồm 9 cuốn sách (giống nhau), 8 cuốn số (giống nhau), và 11 chiếc bút (giống nhau) được phát cho 14 học sinh giỏi, mỗi người nhận được 2 phần thưởng khác loại. An và Bình là hai trong số 14 học sinh được nhận thưởng. Hỏi có bao nhiêu cách phát phần thưởng cho 14 học sinh đó để An và Bình được nhận phần thưởng có loại giống nhau?
Đáp án: 51744
Có 3 loại hình thức nhận thưởng: sách+sổ, sách+bút, sổ+bút
Gọi số học sinh nhận được phần thưởng thuộc 3 loại nói trên lần lượt là x;y;z
\(\Rightarrow\left\{{}\begin{matrix}x+y=9\\x+z=8\\y+z=11\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=6\\z=5\end{matrix}\right.\)
Hay chúng ta có 3 bạn nhận thưởng sách+sổ, 6 bạn nhận sách+bút, 5 bạn nhận sổ+bút
Như vậy có 3 TH để An và Bình nhận thưởng giống nhau là:
- An Bình cùng nhận sách sổ: còn lại 12 bạn, chọn 6 bạn nhận sách bút có \(C_{12}^6\) sách, còn lại 6 bạn, chọn 5 bạn nhận sổ bút có \(C_6^5\) cách, còn 1 bạn, chọn 1 bạn nhận sách sổ có \(C_1^1\) cách \(\Rightarrow C_{12}^6.C_6^5.C_1^1\) cách
- An Bình nhận sách bút: tương tự như trên ta có \(C_{12}^3.C_9^4.C_5^5\) cách
- An Bình nhận bút sổ: \(C_{12}^3.C_9^6.C_3^3\) cách
Tổng: \(51744\) cách
Đúng 3
Bình luận (0)
Gọi a là số học sinh nhận được sách và sổ ; b là số học sinh nhận được sách và bút ; c là số học sinh nhận được sổ và bút. Ta có : \(a+b=9,a+c=8,b+c=11\)
Giải ra ta được \(a=3,b=6,c=5\)
Xét ba trường hợp sau : TH 1 : An và Bình cùng nhận được sách và sổ. Có 3 người cùng nhận được sách và sổ, trong đó có An và Bình. Vì vậy cần chọn ra 1 người trong só 12 học sinh để nhận sách và sổ suy ra có \(C_{12}^1\) cách chọn. Sau đó chọn ra 6 em trong số 11 học sinh còn lại để nhận sách và bút và 5 học sinh còn lại nhận sổ và bút. Vậy số kết quả trong TH này là: \(C_{12}^1.C^6_{12}\)
TH 2 : An và Bình cùng nhận được sách và bút. Lập luận tương tự TH 1 ta có số kết quả trong TH này là : \(C_{12}^4.C_8^3\)
TH 3 : An và Bình cùng nhận được sổ và bút. Số kết quả trong TH này là :\(C_{12}^3.C_9^3\). . Vậy có: \(C_{12}^1.C_{12}^6+C_{12}^4.C_8^3+C_{12}^3.C_9^3=51744\) cách phát phần thưởng thỏa mãn bài toán.
Đáp án: \(51744\)
Đúng 1
Bình luận (3)
Mn giúp em bài 11c và bài 4f với ạ mai em nộp rồi
Riêng bài 4f thì em có tìm được 1 dạng giải nhưng khó hiểu quá, ai có cách nào dễ hiểu hơn thì giúp em với

11c.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}\dfrac{16a-b^2}{4a}=\dfrac{9}{2}\\16a+4b+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2b^2=-4a\\b=-4a-1\end{matrix}\right.\)
\(\Rightarrow2b^2-b=1\Leftrightarrow2b^2-b-1=0\Rightarrow\left[{}\begin{matrix}b=1\Rightarrow a=-\dfrac{1}{2}\\b=-\dfrac{1}{2}\Rightarrow a=-\dfrac{1}{8}\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=-\dfrac{1}{2}x^2+x+4\\y=-\dfrac{1}{8}x^2-\dfrac{1}{2}x+4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
4f.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}1+b+c=0\\\dfrac{4c-b^2}{4}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=-b-1\\c=\dfrac{b^2}{4}-1\end{matrix}\right.\)
\(\Rightarrow\dfrac{b^2}{4}+b=0\)
\(\Rightarrow\left[{}\begin{matrix}b=0\Rightarrow c=-1\\b=-4\Rightarrow c=3\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=x^2-1\\y=x^2-4x+3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Mn giúp em bài này với ạ chỉ là sắp xếp từ lại thành một cậu thôi bài 29 với 30 mn không cần làm đâu ạ mong cao nhân nào giúp đỡ chứ em đang cần gấp lắm ạ
Đọc tiếp
Mn giúp em bài này với ạ chỉ là sắp xếp từ lại thành một cậu thôi bài 29 với 30 mn không cần làm đâu ạ mong cao nhân nào giúp đỡ chứ em đang cần gấp lắm ạ ![]()

what is her mother going to prepare for her bỉthdat party
Đúng 2
Bình luận (0)
there are three sticks of butter in the cupboard
Đúng 2
Bình luận (0)
i have enough food for the first three day of your stay
Đúng 2
Bình luận (1)
giúp em bài 3 với ạ, mn ơi giúp em với

Bài 4:
a: \(A=\left(x-5\right)\left(2x+3\right)-2x\left(x-3\right)+x+7\)
\(=2x^2+3x-10x-15-2x^2+6x+x+7\)
=-8
Đúng 1
Bình luận (0)

























