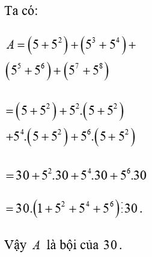chứng tỏ rằng A= 5 + 52 +53 +...+ 520 là bội của 30

Những câu hỏi liên quan
Chứng tỏ rằng: Giá trị của biểu thức
A
5
+
5
2
+
5
3
+
.
.
.
+
5
8
là bội của 30
Đọc tiếp
Chứng tỏ rằng: Giá trị của biểu thức A = 5 + 5 2 + 5 3 + . . . + 5 8 là bội của 30
Ta có: A = 5 + 5 2 + 5 3 + 5 4 + 5 5 + 5 6 + 5 7 + 5 8
= 5 + 5 2 + 5 2 5 + 5 2 + 5 4 5 + 5 2 + 5 6 5 + 5 2
= 30 + 5 2 . 30 + 5 4 . 30 + 5 6 . 30
= 30 . ( 1 + 5 2 + 5 4 + 5 6 ) ⋮ 30
Vậy A là bội của 30
Đúng 2
Bình luận (0)
Chứng tỏ rằng: Giá trị của biểu thức A = 5 + 5 2 + 5 3 + . . . . + 5 8 là bội của 30.
Chứng tỏ rằng:a) Giá trị của biểu thức A
5
+
5
2
+
5
3
+
.
.
.
+
5
8
là bội của 30.b) Giá trị của biểu thức B
3
+...
Đọc tiếp
Chứng tỏ rằng:
a) Giá trị của biểu thức A = 5 + 5 2 + 5 3 + . . . + 5 8 là bội của 30.
b) Giá trị của biểu thức B = 3 + 3 3 + 3 5 + 3 7 + . . . + 3 29 là bội của 273
a, A = 5 + 5 2 + 5 3 + . . . + 5 8
= 5(1+5)+ 5 2 (1+5)+ 5 3 (1+5)+...+ 5 7 (1+5)
= 30+5.30+ 5 2 .30+...+ 5 6 .30
= 30.(1+5+ 5 2 +..+ 5 6 )
Vậy A là bội của 30
b, B = 3 + 3 3 + 3 5 + 3 7 + . . . + 3 29
= 3 1 + 3 2 + 3 4 + 3 7 1 + 3 2 + 3 4 +...+ 3 27 1 + 3 2 + 3 4
= 273+273. 3 6 +...+ 3 26 .273
= 273.(1+ 3 6 +...+ 3 26 )
Vậy B là bội của 273
Đúng 2
Bình luận (0)
Chứng tỏ rằng:a) Giá trị của biểu thức
A
5
+
5
2
+
5
3
+
…
+
5
8
là bội của 30.b) Giá trị của biểu thức
B
3
+
3
3...
Đọc tiếp
Chứng tỏ rằng:
a) Giá trị của biểu thức A = 5 + 5 2 + 5 3 + … + 5 8 là bội của 30.
b) Giá trị của biểu thức B = 3 + 3 3 + 3 5 + 3 7 + … + 3 29 là bội của 273
Chứng minh : A = 5+52+53+...+58 là bội của 30
A = 5 + 52 + 53 +...+ 58
A = (5 + 52) +( 53 + 54) +...+ ( 57 + 58)
A = 30 + 52.(5 + 52) +...+ 56.(5 + 52)
A = 30.( 1 + 52 +...+ 56) (đpcm)
Đúng 1
Bình luận (0)
Chứng tỏ: C = 5 +52+53+...+519+520 chia hết cho 13
\(C=\left(5+5^2+5^3+5^4\right)+\left(5^5+5^6+5^7+5^8\right)...+\left(5^{17}+5^{18}+5^{19}+5^{20}\right)\\ C=5\left(1+5+5^2+5^3\right)+5^5\left(1+5+5^2+5^3\right)...+5^{17}\left(1+5+5^2+5^3\right)\\ C=5\cdot156+5^5\cdot156+...+5^{17}\cdot156\\ C=156\left(5+5^5+...+5^{17}\right)\\ C=12\cdot13\left(5+5^5+...+5^{17}\right)⋮17\)
Đúng 0
Bình luận (0)
(5 +53)+(52+54)...+(518+520)
5(1+52)+52(1+52)+...+518(1+52)
(1+52)(5+52+...+518)
26(5+52+...+518)⋮13
vậy (5 +53)+(52+54)...+(518+520)⋮13
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
A=5-52-53-...-56 là bội của 30
Lời giải:
$A=(5-5^2)-(5^3+5^4)-(5^5+5^6)$
$=5(1-5)-5^4(1+5)-5^5(1+5)$
$=-20-5^4.6-5^5.6=-20-30.5^3-30.5^4$
$=-20-30(5^3+5^4)$ không chia hết cho $30$ cho $20$ không chia hết cho $30$
Do đó $A$ không thể là bội của $30$
Đúng 0
Bình luận (0)
Cho M = 51 + 52 + 53 ... + 519 + 520 + 521
Chứng minh M là bội của 31
Giúp e nha mọi người ![]()
M = 51 + 52 + 53 + ... + 519 + 520 + 521
M = (51 + 52 + 53) + (54 + 55 + 56 ) + ... + (519 + 520 + 521)
M = 5( 1 + 5 + 52) + 54(1 + 5 + 52) + ... + 519(1 + 5 + 52)
M = 5.31 + 54.31 + ... + 519.31
M = 31(5 + 54 + ... + 519) ⋮ 31 (ĐPCM)
Đúng 0
Bình luận (0)
cho biểu thức: M = 5 + 52 + 53 + .........+ 580. chứng tỏ rằng M chia hết cho 30
M=(5+5^2)+...+(5^79+5^80)
M=30.1+...+5^78+(5^1+5^2)
M=30(1+...+5^78) /30
VẬY M / 30
Đúng 0
Bình luận (0)
\(M=5+5^2+5^3+....+5^{80}\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+...+\left(5^{79}+5^{80}\right)\)
\(=30+5^3.\left(5+5^2\right)+...+5^{70}.\left(5+5^2\right)\)
\(=1.30+5^3.30+...+5^{70}.30\)
\(=\left(1+5^3+...+5^{70}\right).30\)
\(=>M⋮30\)
Đúng 1
Bình luận (0)
Cho biểu thức: M 5 + 52 + 53 + … + 580. Chứng tỏ rằng M chia hết cho 30.
Đọc tiếp
Cho biểu thức: M = 5 + 52 + 53 + … + 580. Chứng tỏ rằng M chia hết cho 30.
M=(5+5^2)+5^2(5+5^2)+...+5^78(5+5^2)
=30(1+5^2+...+5^78) chia hết cho 30
Đúng 0
Bình luận (0)