a) 

Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)

Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.

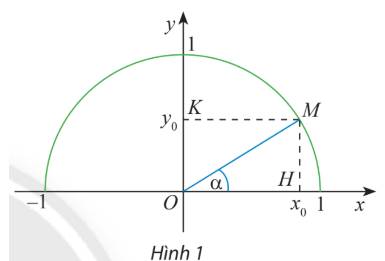
Ta có: tam giác vuông OHM vuông tại H và \(\alpha  = \widehat {xOM}\)

Do đó: \(\sin \alpha  = \frac{{MH}}{{OM}} = MH;\;\cos \alpha  = \frac{{OH}}{{OM}} = OH.\)

\( \Rightarrow {\cos ^2}\alpha  + {\sin ^2}\alpha  = O{H^2} + M{H^2} = O{M^2} = 1\)

b) Ta có:

\(\begin{array}{l}\;\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)

c) Với \(\alpha  \ne {90^o}\) ta có:

\(\begin{array}{l}\;\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha  = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)

d) Ta có:

\(\begin{array}{l}\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha  = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)

Coi BPT là bậc 2 với tham số \(sina;cosa\)

Đặt \(f\left(x\right)=\left(1+sin^2a\right)x^2-2\left(sina+cosa\right)x+1+cos^2a\)

Ta có: \(1+sin^2a>0;\forall a\)

\(\Delta'=\left(sina+cosa\right)^2-\left(1+sin^2a\right)\left(1+cos^2a\right)\)

\(=sin^2a+cos^2a+2sina.cosa-1-sin^2a-cos^2a-sin^2a.cos^2a\)

\(=-sin^2a.cos^2a+2sina.cosa-1\)

\(=-\left(sina.cosa-1\right)^2=-\left(\frac{1}{2}sin2a-1\right)^2\)

\(=-\left(\frac{sin2a-2}{2}\right)^2\)

Do \(sin2a-2< 0;\forall a\Rightarrow\left(\frac{sin2a-2}{2}\right)^2>0;\forall a\)

\(\Rightarrow\Delta'< 0;\forall a\Rightarrow f\left(x\right)>0\) với mọi x và a

Từ M kẻ MP ⊥ Ox, MQ ⊥ Oy

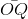=> = cosα; =

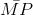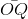
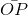= sinα;

Trong tam giác vuông MPO:

MP²+ PO² = OM² => cos² α + sin² α = 1

Ta có:
\(\dfrac{sin\alpha+tan\alpha}{cos\alpha+cot\alpha}=\dfrac{sin\alpha+\dfrac{sin\alpha}{cos\alpha}}{cos\alpha+\dfrac{cos\alpha}{sin\alpha}}\)\(=\dfrac{sin\alpha cos\alpha+sin\alpha}{cos\alpha}:\dfrac{cos\alpha sin\alpha+cos\alpha}{sin\alpha}\)
\(=\dfrac{sin\alpha cos\alpha+sin\alpha}{cos\alpha}.\dfrac{sin\alpha}{cos\alpha sin\alpha+cos\alpha}\)
\(=\dfrac{sin^2\alpha\left(cos\alpha+1\right)}{cos^2\alpha\left(sin\alpha+1\right)}>0\) nếu biểu thức có nghĩa.

a) ta có : \(A=\left(sin\alpha+cos\alpha\right)^2+\left(sin\alpha-cos\alpha\right)^2\)

\(\Leftrightarrow A=sin^2\alpha+2sin\alpha.cos\alpha+cos^2\alpha+sin^2\alpha-2sin\alpha.cos\alpha+cos^2\alpha\)

\(\Leftrightarrow A=2\left(sin^2\alpha+cos^2\alpha\right)=2.1=2\) (không phụ thuộc vào \(\alpha\))

\(\Rightarrow\left(đpcm\right)\)

\(B=sin^6\alpha+cos^6\alpha+3sin^2\alpha.cos^2\alpha\)

\(\Leftrightarrow B=\left(sin^2\alpha+cos^2\alpha\right)^3-3sin^2\alpha.cos^2\alpha\left(sin^2\alpha+cos^2\alpha\right)+3sin^2\alpha.cos^2\alpha\)

\(\Leftrightarrow B=\left(sin^2\alpha+cos^2\alpha\right)^3-3sin^2\alpha.cos^2\alpha+3sin^2\alpha.cos^2\alpha\)

a/A = sin² + 2. sin.cos + cos² + sin² -2cos.sin + cos²= 2

Tớ không biết ghi anpha nên ..

Mình viết luôn là sin với cos, bạn tự cho thêm \(\alpha\) nhé.

VT= \(\sin^2.\dfrac{\sin}{\cos}+\cos^2.\dfrac{\cos}{\sin}+2\sin\cos\)

= \(\dfrac{\sin^3}{\cos}+\dfrac{\cos^3}{\sin}+2\sin\cos\)

= \(\dfrac{\sin^4+\cos^4+2\sin^2.\cos^2}{\cos.\sin}\)

= \(\dfrac{\left(\sin^2+\cos^2\right)^2}{\cos.\sin}\)

= \(\dfrac{1}{\sin.\cos}\)(1)

VP = \(\dfrac{\sin}{\cos}+\dfrac{\cos}{\sin}\)

= \(\dfrac{\sin^2+\cos^2}{\cos.\sin}\)

= \(\dfrac{1}{\cos.\sin}\)(2)

từ (1) và (2) => VT=VP (đpcm)

Chúc bạn học tốt!