Từ M kẻ MP ⊥ Ox, MQ ⊥ Oy
=> 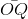 = cosα;
= cosα; 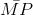 =
= 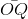
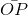 = sinα;
= sinα;
Trong tam giác vuông MPO:
MP2+ PO2 = OM2 => cos2 α + sin2 α = 1
Từ M kẻ MP ⊥ Ox, MQ ⊥ Oy
=> 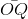 = cosα;
= cosα; 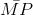 =
= 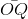
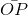 = sinα;
= sinα;
Trong tam giác vuông MPO:
MP2+ PO2 = OM2 => cos2 α + sin2 α = 1
Chứng minh rằng biểu thức sau đây không phụ thuộc vào \(\alpha\) :
a) \(A=\left(\sin\alpha+\cos\alpha\right)^2+\left(\sin\alpha-\cos\alpha\right)^2\)
b) \(B=\sin^4\alpha-\cos^4\alpha-2\sin^2\alpha+1\)
Với những giá trị nào của góc \(\alpha\) (\(0^0\le\alpha\le180^0\)) thì :
a) \(\sin\alpha\) và \(\cos\alpha\) cùng dấu ?
b) \(\sin\alpha\) và \(\cos\alpha\) khác dấu ?
c) \(\sin\alpha\) và \(\tan\alpha\) cùng dấu ?
d) \(\sin\alpha\) và \(\tan\alpha\) khác dấu ?
Chứng minh rằng với \(0^0\le x\le180^0\) ta có :
a) \(\left(\sin x+\cos x\right)^2=1+2\sin x\cos x\)
b) \(\left(\sin x-\cos x\right)^2=1-2\sin x\cos x\)
c) \(\sin^4x+\cos^4x=1-2\sin^2x\cos^2x\)
Cho \(\sin\alpha=\sqrt{3}\cos\alpha\) và 0 < π < π/2
Tìm \(\sin\alpha,\cos\alpha\)
Cho \(\tan\alpha=-2\sqrt{2}\) với \(0^0< \alpha< 90^0\). Tính \(\sin\alpha\) và \(\cos\alpha\) ?
\(B=\dfrac{\sin^2\alpha-2.\sin\alpha.\cos\alpha+3.\cos^2\alpha}{2.\sin^2\alpha+\sin\alpha.\cos\alpha-2\cos^2\alpha}\)
Cho \(\sin\alpha=\dfrac{1}{4}\) với \(90^0< \alpha< 180^0\). Tính \(\cos\alpha\) và \(\tan\alpha\) ?
1) Cho \(\tan\alpha=\dfrac{1}{4}\) và \(0^o< \alpha< 90^o\). Tính giá trị biểu thức \(a=2\sin^2\alpha+\cos^2\alpha\)
Giúp mình với mình tick cho !
Rút gọn biểu thức \(P=\dfrac{1}{\sin\alpha.\sin2\alpha}+\dfrac{1}{\sin2\alpha.\sin3\alpha}+.....+\dfrac{1}{\sin n\alpha.\sin\left(n+1\right)\alpha}\)
(Giúp mik với !!!)