Rút gọn biểu thức:
B = (1+ tan2a).(1- sin2a) \(-\)(1+ cotg2a).(1- cos2a)
rút gọn
\(\dfrac{sin2a+1}{cos2a}-\dfrac{1-sin2a}{sina-cosb}\)
Tính sin2a, cos2a, tan2a biết
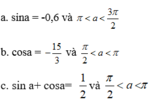
Chứng minh tan2a - sin2a .tan2a=(1-cos a)(1+cos a)
\(\tan^2\alpha-\sin^2\alpha\cdot\tan^2\alpha\)
\(=\tan^2\alpha\cdot\left(1-\cos^2\alpha\right)\)
\(=\tan^2\alpha\cdot\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)\)
\(\tan^2\alpha-\sin^2\alpha\cdot\tan^2\alpha\\ =\tan^2\alpha\left(1-\sin^2\alpha\right)=\tan^2\alpha\cdot\cos^2\alpha\\ =\dfrac{\sin^2\alpha}{\cos^2\alpha}\cdot\cos^2\alpha=\sin^2\alpha\\ =1-\cos^2\alpha=\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)\)
Thu gọn biểu thức:
A=sin2x+sin4x+sin6x+sin8x
B=\(\frac{sin2a-2sin4a+sin6a}{1+cos2a+cos4a}\)
C=\(\frac{cos5a.cos3a+sin7a.sina}{sin6a+sin2a}\)
Cm:\(\dfrac{1+cos2a+sin2a}{1+sin2a-cos2a}=tana\)
\(VT=\dfrac{1+\cos^2a-\sin^2a+2\cdot\sin a\cdot\cos a}{1+2\cdot\sin a\cdot\cos a-\cos^2a+\sin^2a}\)
\(=\dfrac{2\cdot\cos^2a+2\cdot\sin a\cdot\cos a}{2\cdot\sin^2a+2\cdot\sin a\cdot\cos a}\)
\(=\dfrac{2\cdot\cos a\left(\cos a+\sin a\right)}{2\cdot\sin a\cdot\left(\sin a+\cos a\right)}\)
\(=\dfrac{\cos a}{\sin a}=\cot a\)
Câu 1 : chứng minh rằng : \(\frac{sina+sin2a+sin3a}{cosa+cos2a+cos3a}=tan2a\)
Câu 2 : chứng minh : \(cos^2\left(\alpha-\frac{\pi}{4}\right)-sin^2\left(\alpha-\frac{\pi}{4}\right)=sin2\alpha\)
\(\frac{sina+sin3a+sin2a}{cosa+cos3a+cos2a}=\frac{2sin2a.cosa+sin2a}{2cos2a.cosa+cos2a}=\frac{sin2a\left(2cosa+1\right)}{cos2a\left(2cosa+1\right)}=\frac{sin2a}{cos2a}=tan2a\)
\(cos^2\left(a-\frac{\pi}{4}\right)-sin^2\left(a-\frac{\pi}{4}\right)=cos\left(2a-\frac{\pi}{2}\right)\)
\(=cos\left(\frac{\pi}{2}-2a\right)=sin2a\)
Rút gọn biểu thức:
B=\(\dfrac{3}{x-1}.\sqrt{\dfrac{x^2-2x+1}{9x^2}}\)với 0<x<1
Lời giải:
\(B=\frac{3}{x-1}\sqrt{\frac{(x-1)^2}{(3x)^2}}=\frac{3}{x-1}|\frac{x-1}{3x}|\)
\(=\frac{3}{x-1}.\frac{1-x}{3x}=\frac{-1}{x}\)
\(B=\dfrac{3}{x-1}.\sqrt{\dfrac{x^2-2x+1}{9x^2}}=\dfrac{3}{x-1}.\sqrt{\left(\dfrac{x-1}{3x}\right)^2}\)
\(=\dfrac{3}{x-1}.\left|\dfrac{x-1}{3x}\right|=\dfrac{3}{x-1}.\dfrac{1-x}{3x}=-\dfrac{1}{x}\)
Cho cosa = 3/4 vào 270°<a<370° . Tính
A sina , tana , cota
B sin2a , cos2a , tan2a
B sin( a+ π\3 )
Nêu điều kiện xác định và rút gọn biểu thức:B=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
đk : x >= 0 ; x khác 1
\(B=\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2}{x-1}=\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{x-1}=\dfrac{4\sqrt{x}}{x-1}\)
B xác định \(< =>\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
\(B=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2}{x-1}=\dfrac{x+2\sqrt{x}+1-\left(x-2\sqrt{x}+1\right)}{x-1}=\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{x-1}=\dfrac{4\sqrt{x}}{x-1}\)
ĐKXĐ:\(\left\{{}\begin{matrix}x\ge0\\\sqrt{x}-1\ne0\\\sqrt{x}+1\ne0\left(luôn.đúng\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt{x}\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\\ =\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)