a) thu gọn và viet đã thực thể chiều giảm dần của biến ;
P(x) : 2x^3-3x+x^5-4x^3+4x-x^6+x^2-2
Q(x): x^3-2x^2+3x+2x^2
b) Tính P(x)+Q(x);P(x)-Q(x)
c) Gọi M(x)=P(x)+Q(x) tìm bậc của M(x).
Các bạn làm ơn giúp mk với
Cho hai đa thức A(x) = 5 +3x2 – x - 2x2 và B(x) = 3x + 3 – x – x2
Thu gọn và sắp xếp hai đa thức theo lũy thừa giảm dần của biến.
Thu gọn
A(x) = 5 +3x2 – x - 2x2
A(x) = 5+x2-x
A(x) = x2-x+5
B(x) = 3x + 3 – x – x2
B(x) = ( 3x-x) + 3 - x2
B(x) = 2x+3-x2
B(x)= -x2 + 2x+3
\(A(x) = 5 +3x^2 – x - 2x^2 = 5 + ( 3^2 - 2x^2 ) - x = x^2 -x+5\)
\( B(x) = 3x + 3 – x – x^2 = ( 3x-x ) + 3 - x^2 = 2x + 3 - x^2 = -x^2 + 2x +3\)
Cho đa thức 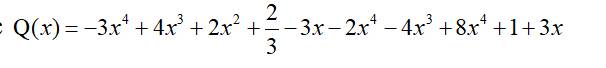
a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến.
b) Tìm bậc và các hệ số của Q(x).
c) Chứng tỏ Q(x) không có nghiệm.
`a,`
`Q(x)=`\(-3x^4+4x^3+2x^2+\)\(\dfrac{2}{3}-3x-2x^4-4x^3+8x^4+1+3x\)
`=(-3x^4-2x^4+8x^4)+(4x^3-4x^3)+2x^2+(-3x+3x)+(2/3+1)`
`= 3x^4+2x^2+5/3`
`b,`
Bậc của đa thức: `4`
Hệ số cao nhất: `3`
Hệ số tự do: `5/3`
`c,`
Đặt `3x^4+2x^2+5/3=0`
Vì \(\left\{{}\begin{matrix}x^4\ge0\rightarrow3x^4\ge0\\x^2\ge0\rightarrow2x^2\ge0\end{matrix}\right.\)
`-> 3x^4+2x^2+5/3`\(>0\)
`->` Đa thức `Q(x)` vô nghiệm.
`@`\(\text{dn inactive.}\)
Cho đa thức:
\(A=x^4+2\left(3x^2-x\right)-2x^3+5x+2\)
Thu gọn và sắp xếp đa thức theo lũy thừa giảm dần của biến.
+ Thu gọn :
\(A=x^4+6x^2-2x-2x^3+5x+2\)
\(=x^4+6x^2-2x^3+3x+2\)
+ Sắp xếp giảm dần :
\(A=x^4-2x^3+6x^2+3x+2\)
1. Thu gọn đơn thức sau, cho biết phần hệ số, phần biến, bậc của đơn thức(x,y là biến)
a. -ax(xy3)2(-by)3
b. xy(-ax)2(-by)3
2. Thu gọn và sắp xếp đa thức sau theo lũy thừa giảm dần của biến
P(x)= 5x-4x4+x6+3-2x3-7x-x7+1-2x6+3x3+x7
2.
Bài 1:
a) Ta có: \(-ax\left(xy^3\right)^2\cdot\left(-by\right)^3\)
\(=-a\cdot x\cdot x^2\cdot y^6\cdot\left(-b\right)^3\cdot y^3\)
\(=abx^3y^9\)
b) Ta có: \(xy\cdot\left(-ax\right)^2\cdot\left(-by\right)^3\)
\(=xy\cdot a^2\cdot x^2\cdot b^3\cdot y^3\)
\(=a^2b^3x^3y^4\)
Bài 2:
Ta có: \(P\left(x\right)=5x-4x^4+x^6+3-2x^3-7x-x^7+1-2x^6+3x^3+x^7\)
\(=\left(-x^7+x^7\right)+\left(x^6-2x^6\right)-4x^4+\left(-2x^3+3x^3\right)+\left(5x-7x\right)+\left(3+1\right)\)
\(=-x^6-4x^4+x^3-2x+4\)
1. Thu gọn đơn thức sau, cho biết phần hệ số, phần biến, bậc của đơn thức(x,y là biến)
a. -ax(xy3)2(-by)3
b. xy(-ax)2(-by)3
Giải :
a. \(-ax\left(xy^3\right)^2\left(-by\right)^3=-a\cdot x\cdot x^2\cdot\left(y^3\right)^2\cdot\left(-b\right)^3\cdot y^3=-a\cdot\left(-b\right)^3\cdot\left(x\cdot x^2\right)\cdot\left(y^6\cdot y^3\right)=ab^3x^3y^9\)
Phần hệ số : ab3 . Phần biến x3y9
Bậc của đơn thức : 3+9=12
b. \(xy\left(-ax\right)^2\left(-by\right)^3=-a^2b^3x^3y^3\)
Phần hệ số : -a2b3. phần biến x3y3
Bậc : 3+3=6
Cho đa thức: P(x) = 2x4 + 5x3 – 2x2 + 4x2 – x4 – 4x3 + 2 – x4
a/ Thu gọn và sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm dần của biến.
b/ Tính P(1) và P(-1)
Thu gọn và sắp xếp các hạng tử của đa thức theo lũy thừa giảm dần của biến: P(x)=x3+2x2+2
P(1)=13+2.12+2=1+2+2=5
P(-1)=(-1)3+2.(-1)2+2=(-1)+2+2=3
bài 1:
b, thực hiện phép nhân (x mũ2 -8) . (x mũ 3 +2x + 4)
bài 2:
cho đa thức A(x)= -5/3 x mũ 2+ 3/4 x mũ 4 + 2x - 7/3 x mũ 2 -2+4x +1/4x mũ 4
a, thu gọn và sắp xếp đa thức A(x) theo lũy thừa giảm dần của biến
b,tìm bậc và hệ số cao nhất của A(x)
Bài 1:
(x² - 8)(x³ + 2x + 4)
= x².x³ + x².2x + x².4 - 8.x³ - 8.2x - 8.4
= x⁵ + 2x³ + 4x² - 8x³ - 16x - 32
= x⁵ - 6x³ + 4x² - 16x - 32
Bài 2
a) A(x) = -5/3 x² + 3/4 x⁴ + 2x - 7/3 x² - 2 + 4x + 1/4 x⁴
= (3/4 x⁴ + 1/4 x⁴) + (-5/3 x² - 7/3 x²) + (2x + 4x) - 2
= x⁴ - 4x² + 6x - 2
b) Bậc của A(x) là 4
Hệ số cao nhất là 1
`1,`
`b,`
`(x^2-8)(x^3+2x+4)`
`= x^2(x^3+2x+4)-8(x^3+2x+4)`
`= x^5+2x^3+4x^2-8x^3-16x-12`
`= x^5-6x^3+4x^2-16x-12`
`2,`
`a,`
`A(x)=-5/3x^2 + 3/4x^4 + 2x - 7/3x^2 - 2 + 4x + 1/4x^4`
`= (3/4x^4+1/4x^4)+(-5/3x^2-7/3x^2)+(2x+4x)-2`
`= x^4-4x^2+6x-2`
`b,`
Bậc của đa thức: `4`
Hệ số cao nhất: `1`.
Cho A (x)=x^2 -2x +1 và B(x)= 3x^2 + x -x^2 -5 A, thu gọn và sắp xếp đa thức theo lũy thừa giảm dần của biến B Tính A (x) + B (x) C tính A (x) - B(x)
cho đa thức :
A(x)= -45-x3+4x2 +5x+9+4x5-6x2-2
a)Thu gọn đa thức trên rồi sắp xếp chúng thep lũy thừa giảm dần , tăng dần của biến
b) Tìm bậc của đa thức trên
`a)`
`@` Giảm dần:
`A(x)=-4^5-x^3+4x^2+5x+9+4x^5-6x^2-2`
`A(x)=4x^5-x^3-2x^2+5x-1017`
`@` Tăng dần:
`A(x)=-4^5-x^3+4x^2+5x+9+4x^5-6x^2-2`
`A(x)=-1017+5x-2x^2-x^3+4x^5`
_______________________________________________________
`b)` Bậc của `A(x)` là: `5`