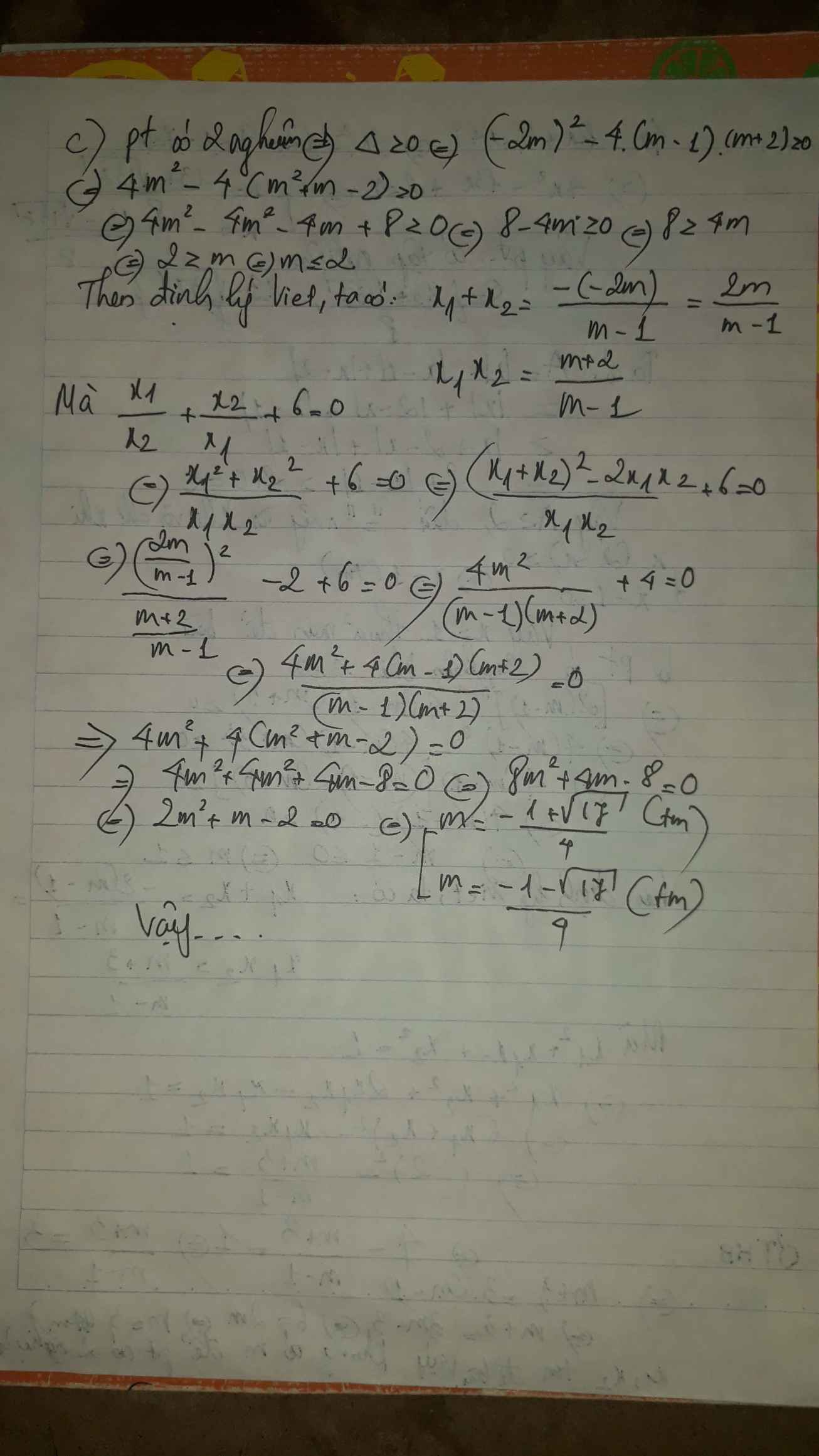a. để phương trình có 2 nghiệm phân biệt thì △ > 0

\(\text{△}=b^2-4ac=\left[-2\cdot\left(m-1\right)\right]^2-4\cdot1\cdot\left(4m+1\right)\\ \text{△}=4\cdot\left(m-1\right)^2-4\cdot\left(4m+1\right)\\ \text{△}=4\cdot\left[\left(m-1\right)^2-\left(4m+1\right)\right]\\ \text{△}=4\cdot\left[m^2-2m+1-4m-1\right]\\ \text{△}=4\cdot\left[m^2-m\right]=4m\cdot\left(m-6\right)\)

vậy m > 6 hoặc m < 0

b. áp dụng định lý vi-et ta có:

\(x_1+x_2=-b< =>2\left(m-1\right)\\ x_1x_2=c< =>4m+1\)

theo đề: \(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=5\)

\(=>\left[2\left(m-1\right)\right]^2-2\left(4m+1\right)=5\\ 4\left(m-1\right)^2-2\left(4m+1\right)=5\\ 4\left(m^2-2m+1\right)-8m-2=5\\ 4m^2-8m+4-8m-2=5\\ 4m^2-16m-3=0\\ =>\left[{}\begin{matrix}m=\dfrac{4+\sqrt{19}}{2}\left(KTM\right)\\m=\dfrac{4-\sqrt{19}}{2}\left(TM\right)\end{matrix}\right.\)

vậy m cần tìm là: \(\dfrac{4-\sqrt{19}}{2}\)

Δ=(m+2)^2-4*2m=(m-2)^2

Để PT có hai nghiệm pb thì m-2<>0

=>m<>2

\(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1x_2}{4}\)

=>\(\dfrac{x_1+x_2}{x_1x_2}=\dfrac{x_1x_2}{4}\)

=>\(\dfrac{m+2}{2m}=\dfrac{2m}{4}=\dfrac{m}{2}\)

=>2m^2=2m+4

=>m^2-m-2=0

=>m=2(loại) hoặc m=-1

b) phương trình có 2 nghiệm  \(\Leftrightarrow\Delta'\ge0\)

\(\Leftrightarrow\left(m-1\right)^2-\left(m-1\right)\left(m+3\right)\ge0\)

\(\Leftrightarrow m^2-2m+1-m^2-3m+m+3\ge0\)

\(\Leftrightarrow-4m+4\ge0\)

\(\Leftrightarrow m\le1\)

Ta có: \(x_1^2+x_1x_2+x_2^2=1\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=1\)

Theo viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\left(m-1\right)\\x_1x_2=\dfrac{c}{a}=m+3\end{matrix}\right.\)

\(\Leftrightarrow\left[-2\left(m-1\right)^2\right]-2\left(m+3\right)=1\)

\(\Leftrightarrow4m^2-8m+4-2m-6-1=0\)

\(\Leftrightarrow4m^2-10m-3=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m_1=\dfrac{5+\sqrt{37}}{4}\left(ktm\right)\\m_2=\dfrac{5-\sqrt{37}}{4}\left(tm\right)\end{matrix}\right.\Rightarrow m=\dfrac{5-\sqrt{37}}{4}\)

Câu c:

b1: tìm đk m t/m: Δ>0 ↔ m∈(\(\dfrac{1-\sqrt{10}}{2}\) ; \(\dfrac{1+\sqrt{10}}{2}\))

b2: ➝x1+x2 =-2m-1 (1)

      → x1.x2=m^2-1 (2)

b3: biến đổi : (x1-x2)^2 = x1-5x2

↔ (x1+x2)^2 -4.x1.x2 -(x1+x2) +6.x2=0

↔4.m^2 +4m +1 - 4.m^2 +4 +2m+1+6. x2=0

↔x2= -m-1

B4: thay x2= -m-1 vào (1) → x1 = -m

     Thay x2 = -m-1, x1 = -m vào (2) 

→m= -1

B5: thử lại:

Với m= -1 có pt: x^2 -x =0

Có 2 nghiệm x1=1 và x2=0 (thoả mãn)

pt sai 

Để pt có 2 nghiệm pb khác 0:

\(\left\{{}\begin{matrix}\Delta'=4\left(m-1\right)^2-3\left(m^2-4m+1\right)>0\\x_1x_2=\dfrac{m^2-4m+1}{3}\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m^2+4m+1>0\\m^2-4m+1\ne0\end{matrix}\right.\) (1)

Theo hệ thức Viet:  \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{4\left(m-1\right)}{3}\\x_1x_2=\dfrac{m^2-4m+1}{3}\end{matrix}\right.\)

\(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{1}{2}\left(x_1+x_2\right)\Leftrightarrow\dfrac{x_1+x_2}{x_1x_2}=\dfrac{1}{2}\left(x_1+x_2\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x_1+x_2=0\\x_1x_2=2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\dfrac{4\left(m-1\right)}{3}=0\\\dfrac{m^2-4m+1}{3}=2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-1\\m=5\end{matrix}\right.\) 

Thế vào hệ điều kiện (1) kiểm tra chỉ có \(\left[{}\begin{matrix}m=1\\m=5\end{matrix}\right.\) thỏa mãn

d: Ta có: \(\text{Δ}=\left(m+1\right)^2-4\cdot2\cdot\left(m+3\right)\)

\(=m^2+2m+1-8m-24\)

\(=m^2-6m-23\)

\(=m^2-6m+9-32\)

\(=\left(m-3\right)^2-32\)

Để phương trình có hai nghiệm phân biệt thì \(\left(m-3\right)^2>32\)

\(\Leftrightarrow\left[{}\begin{matrix}m-3>4\sqrt{2}\\m-3< -4\sqrt{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m>4\sqrt{2}+3\\m< -4\sqrt{2}+3\end{matrix}\right.\)

Áp dụng hệ thức Vi-et, ta được:

\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{m+1}{2}\\x_1x_2=\dfrac{m+3}{2}\end{matrix}\right.\)

Ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{m+1}{2}\\x_1-x_2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1=\dfrac{m+3}{2}\\x_2=x_1-1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{m+3}{4}\\x_2=\dfrac{m+3}{4}-\dfrac{4}{4}=\dfrac{m-1}{4}\end{matrix}\right.\)

Ta có: \(x_1x_2=\dfrac{m+3}{2}\)

\(\Leftrightarrow\dfrac{\left(m+3\right)\left(m-1\right)}{16}=\dfrac{m+3}{2}\)

\(\Leftrightarrow\left(m+3\right)\left(m-1\right)=8\left(m+3\right)\)

\(\Leftrightarrow\left(m+3\right)\left(m-9\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=-3\\m=9\end{matrix}\right.\)

a: \(\Delta=\left(2m-2\right)^2-4\left(-m-3\right)\)

\(=4m^2-8m+4+4m+12\)

\(=4m^2-4m+16\)

\(=\left(2m-1\right)^2+15>0\)

Do đó: Phương trình luôn có hai nghiệm phân biệt

b: Theo đề, ta có:

\(\left(x_1+x_2\right)^2-2x_1x_2>=10\)

\(\Leftrightarrow\left(2m-2\right)^2-2\left(-m-3\right)>=10\)

\(\Leftrightarrow4m^2-8m+4+2m+6-10>=0\)

\(\Leftrightarrow4m^2-6m>=0\)

=>m<=0 hoặc m>=3/2

a, x = 3 , x= -1

b, m = 3 , m = 1