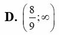Question

Tìm \(m\) để phương trình \(4^x-2^{x+1}+m+2=0\) có 2 nghiệm phân biệt \(x_1\), \(x_2\) \(>-1\).

Answer 1

Đặt \(t=2^x\Rightarrow\) pt trở thành \(t^2-2t+m+2=0\Rightarrow t^2-2t=-m-2\left(1\right)\) 

Với mỗi nghiệm t ta sẽ có một nghiệm x

Vì \(x>-1\) nên \(t=2^x>\dfrac{1}{2}\)

Để pt của đề bài có 2 nghiệm phân biệt \(x_1,x_2>-1\) thì pt (1) có 2 nghiệm phân biệt  \(t_1,t_2>\dfrac{1}{2}\)

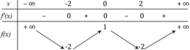
bbt:

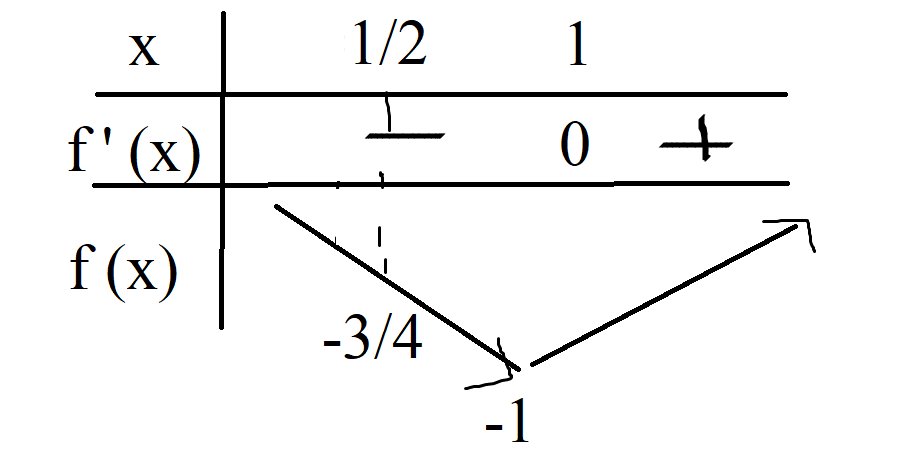
Theo bbt \(\Rightarrow-1< -m-2< -\dfrac{3}{4}\Rightarrow-\dfrac{5}{4}< m< -1\)