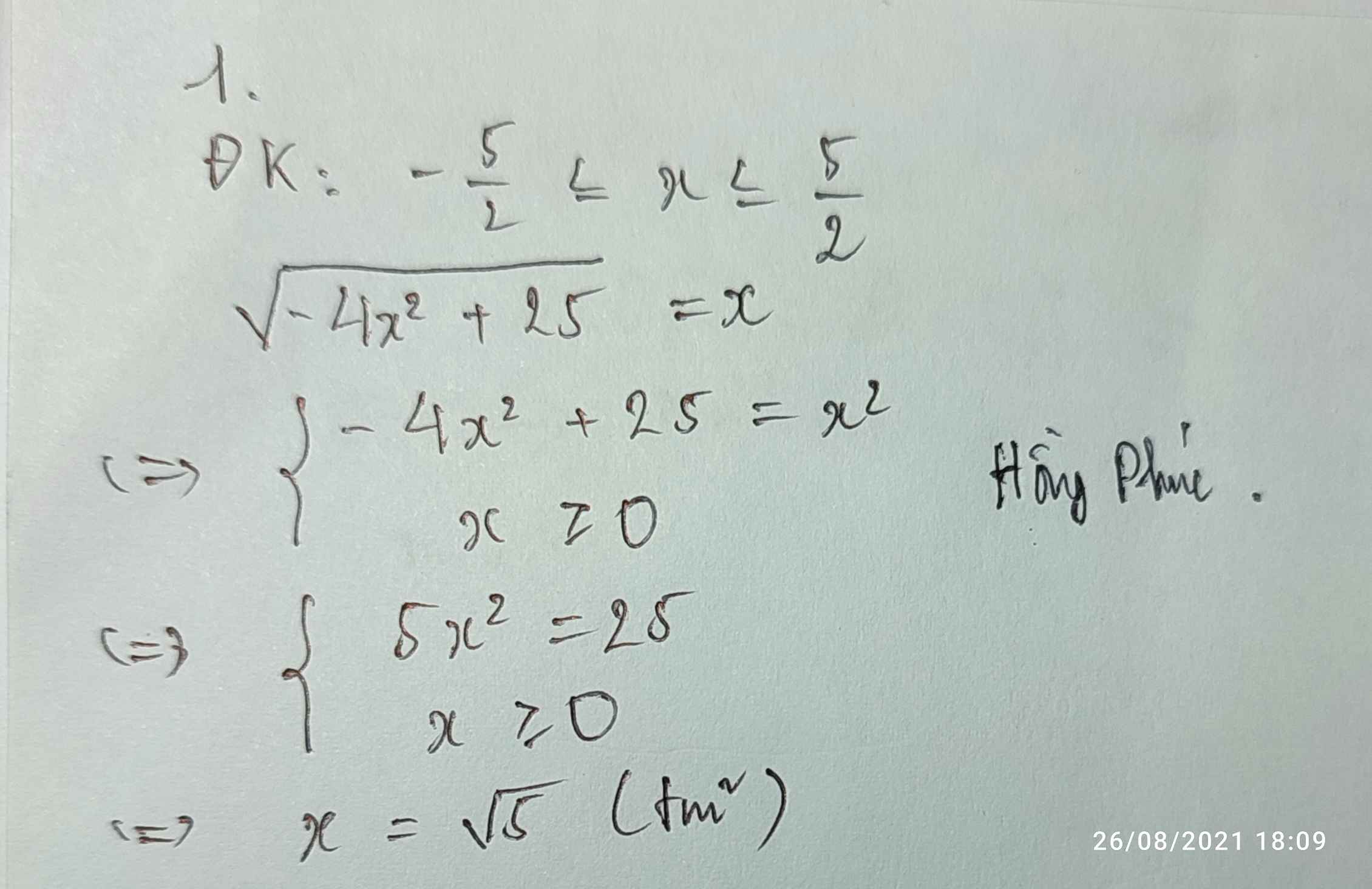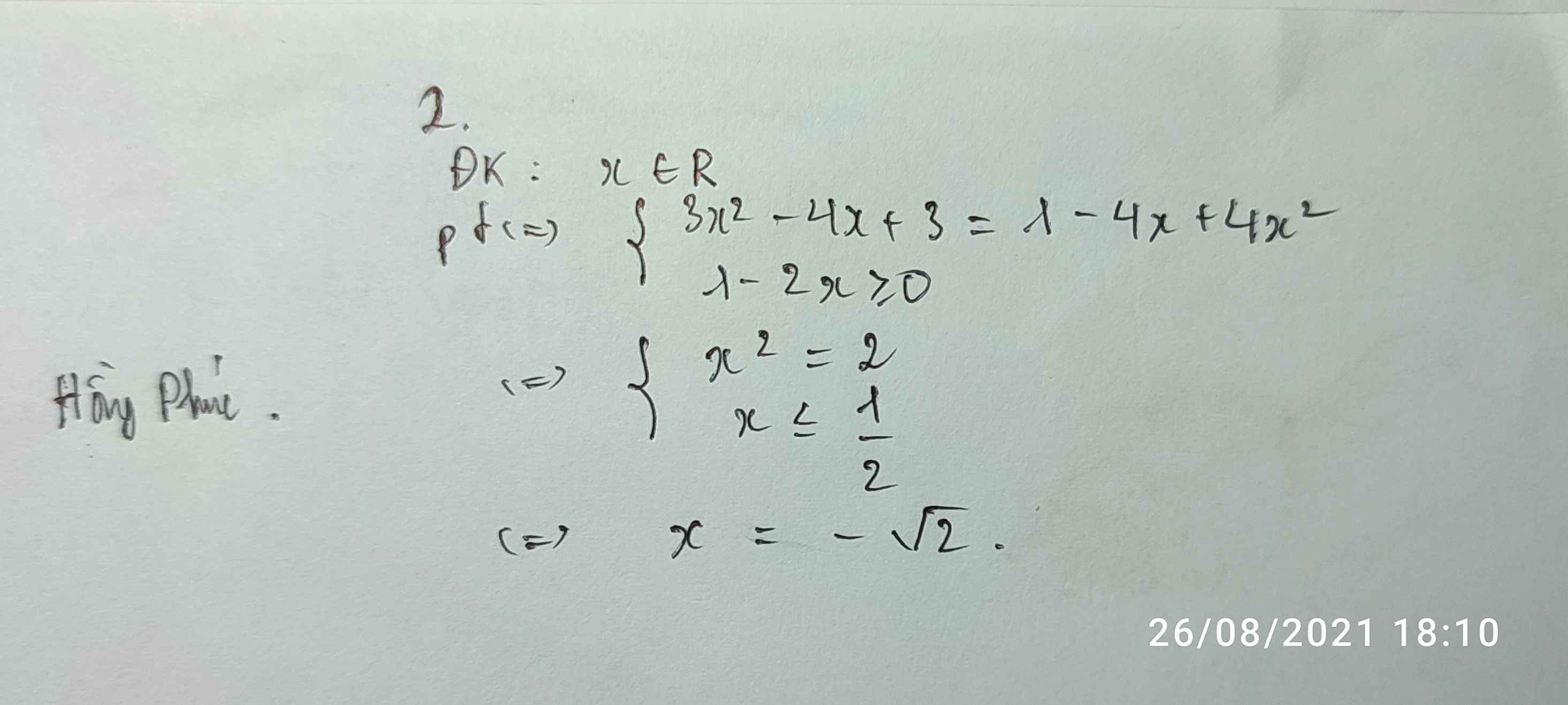sqrt(x + 3) + sqrt(5 - x) + 6sqrt((x + 3)(5 - x)) = 2

Những câu hỏi liên quan
Rút gọn : Chi tiết giúp e, e xin cảm ơn ạ
O = (x + 6sqrt(x))/(sqrt(x + 6)) + sqrt(x)
\(=\sqrt{x}+\sqrt{x}=2\sqrt{x}\)
Đúng 1
Bình luận (0)
Giải phương trình:1. sqrt{dfrac{42}{5-x}}+sqrt{dfrac{60}{7-x}}62. sqrt{x^2-3x+2}+sqrt{x+3}sqrt{x-2}+sqrt{x^2+2x-3}3. x^2+x+12sqrt{x+1}364. sqrt{x+2}-sqrt{x-6}25. sqrt[3]{x-1}-sqrt[3]{x-3}sqrt[3]{2}6. 5sqrt{1+x^3}2left(x^2+2right)6. left(sqrt{x+5}-sqrt{x+2}right)left(1+sqrt{x^2+7x+10}right)3
Đọc tiếp
Giải phương trình:
1. \(\sqrt{\dfrac{42}{5-x}}+\sqrt{\dfrac{60}{7-x}}=6\)
2. \(\sqrt{x^2-3x+2}+\sqrt{x+3}=\sqrt{x-2}+\sqrt{x^2+2x-3}\)
3. \(x^2+x+12\sqrt{x+1}=36\)
4. \(\sqrt{x+2}-\sqrt{x-6}=2\)
5. \(\sqrt[3]{x-1}-\sqrt[3]{x-3}=\sqrt[3]{2}\)
6. \(5\sqrt{1+x^3}=2\left(x^2+2\right)\)
6. \(\left(\sqrt{x+5}-\sqrt{x+2}\right)\left(1+\sqrt{x^2+7x+10}\right)=3\)
1.
ĐKXĐ: \(x< 5\)
\(\Leftrightarrow\sqrt{\dfrac{42}{5-x}}-3+\sqrt{\dfrac{60}{7-x}}-3=0\)
\(\Leftrightarrow\dfrac{\dfrac{42}{5-x}-9}{\sqrt{\dfrac{42}{5-x}}+3}+\dfrac{\dfrac{60}{7-x}-9}{\sqrt{\dfrac{60}{7-x}}+3}=0\)
\(\Leftrightarrow\dfrac{9x-3}{\left(5-x\right)\left(\sqrt{\dfrac{42}{5-x}}+3\right)}+\dfrac{9x-3}{\left(7-x\right)\left(\sqrt{\dfrac{60}{7-x}}+3\right)}=0\)
\(\Leftrightarrow\left(9x-3\right)\left(\dfrac{1}{\left(5-x\right)\left(\sqrt{\dfrac{42}{5-x}}+3\right)}+\dfrac{1}{\left(7-x\right)\left(\sqrt{\dfrac{60}{7-x}}+3\right)}\right)=0\)
\(\Leftrightarrow x=\dfrac{1}{3}\)
Đúng 2
Bình luận (0)
b.
ĐKXĐ: \(x\ge2\)
\(\sqrt{\left(x-2\right)\left(x-1\right)}+\sqrt{x+3}=\sqrt{x-2}+\sqrt{\left(x-1\right)\left(x+3\right)}\)
\(\Leftrightarrow\sqrt{\left(x-2\right)\left(x-1\right)}-\sqrt{x-2}+\sqrt{x+3}-\sqrt{\left(x-1\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\sqrt{x-2}\left(\sqrt{x-1}-1\right)-\sqrt{x+3}\left(\sqrt{x-1}-1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)\left(\sqrt{x-2}-\sqrt{x+3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-1}-1=0\\\sqrt{x-2}-\sqrt{x+3}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=1\\x-2=x+3\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=2\)
Đúng 2
Bình luận (0)
3.
ĐKXĐ: \(x\ge-1\)
\(x^2+x-12+12\left(\sqrt{x+1}-2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+4\right)+\dfrac{12\left(x-3\right)}{\sqrt{x+1}+2}=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+4+\dfrac{12}{\sqrt{x+1}+2}\right)=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
1) x-\(7\sqrt{x-3}\) -9=0 2) \(\sqrt{x+3}\) =5-\(\sqrt{x-2}\) 3) \(\sqrt{x-4\sqrt{x+4}}\) =3 4) \(\sqrt{8-\dfrac{2}{3}x}-5\sqrt{2}\) =0 5) \(\sqrt{x^2-4x+4}\) =2-x
1, \(K=\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\)
2, \(\sqrt{x-3}-2.\sqrt{x^2-3x}=0\)
3, \(\dfrac{9x-7}{\sqrt{7x+5}}=\sqrt{7x+5}\)
4, \(x-5\sqrt{x}+4=0\)
1,\(K=\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{x}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{6-2\sqrt{5}}+\sqrt{6+2\sqrt{5}}\right)\)\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{5}-1\right)^2}+\sqrt{\left(\sqrt{5}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\left|\sqrt{5}-1\right|+\sqrt{5}+1\right)\)\(=\dfrac{1}{\sqrt{2}}\left|\sqrt{5}-1+\sqrt{5}+1\right|=\dfrac{1}{\sqrt{2}}.2\sqrt{5}\)\(=\sqrt{10}\)
2, \(\sqrt{x-3}-2\sqrt{x^2-3x}=0\left(đk:x\ge3\right)\)
\(\Leftrightarrow\sqrt{x-3}\left(1-2\sqrt{x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\1-2\sqrt{x}=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\left(ktm\right)\end{matrix}\right.\)
Vậy pt có nghiệm x=3
3, \(\dfrac{9x-7}{\sqrt{7x+5}}=\sqrt{7x+5}\left(đk:x>-\dfrac{5}{7}\right)\)
\(\Leftrightarrow9x-7=7x+5\)
\(\Leftrightarrow x=6\left(tm\right)\)
4, \(x-5\sqrt{x}+4=0\)(đk: \(x\ge0\))
\(\Leftrightarrow\left(\sqrt{x}-1\right)\left(\sqrt{x}-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=16\end{matrix}\right.\) (tm)
Vậy...
Đúng 2
Bình luận (0)
1) Bạn tự làm
2) ĐK: \(x\ge3\)
PT \(\Leftrightarrow\sqrt{x-3}\left(1-2\sqrt{x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\2\sqrt{x}=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{4}\left(loại\right)\end{matrix}\right.\)
Vậy ...
3) ĐK: \(x>-\dfrac{5}{7}\)
PT \(\Rightarrow9x-7=7x+5\) \(\Leftrightarrow x=6\)
Vậy ...
4) ĐK: \(x\ge0\)
PT \(\Leftrightarrow x-4\sqrt{x}-\sqrt{x}+4=0\)
\(\Leftrightarrow\left(\sqrt{x}-4\right)\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=4\\\sqrt{x}=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=1\end{matrix}\right.\)
Vậy ...
Đúng 1
Bình luận (0)
Giair phương trình:1) sqrt[5]{32-x^2}-sqrt[5]{1-x^2}42) sqrt{x}+sqrt[4]{20-x}43) x^3+12sqrt{3x-1}4) sqrt[3]{x-1}+3sqrt[4]{82-x}5) a.left(x+3sqrt{x}+2right)left(x+9sqrt{x}+18right)168xb.sqrt{5x^2+14x+9}-sqrt{x^2-x-20}5sqrt{x+1}
Đọc tiếp
Giair phương trình:
1) \(\sqrt[5]{32-x^2}-\sqrt[5]{1-x^2}=4\)
2) \(\sqrt{x}+\sqrt[4]{20-x}=4\)
3) \(x^3+1=2\sqrt{3x-1}\)
4) \(\sqrt[3]{x-1}+3=\sqrt[4]{82-x}\)
5)
\(a.\left(x+3\sqrt{x}+2\right)\left(x+9\sqrt{x}+18\right)=168x\)
\(b.\sqrt{5x^2+14x+9}-\sqrt{x^2-x-20}=5\sqrt{x+1}\)
a) ĐKXĐ: \(x\ge0\)
Ta có: \(\left(x+3\sqrt{x}+2\right)\left(x+9\sqrt{x}+18\right)=168x\)
\(\Leftrightarrow\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)\left(\sqrt{x}+6\right)=168x\)
\(\Leftrightarrow\left(x+6\right)^2+12\sqrt{x}\left(x+6\right)-133=0\)
\(\Leftrightarrow\left(x+6\right)^2+19\sqrt{x}\left(x+6\right)-7\sqrt{x}\left(x+6\right)-133=0\)
\(\Leftrightarrow\left(x+6\right)\left(x+19\sqrt{x}+6\right)-7\sqrt{x}\left(x+19\sqrt{x}+6\right)=0\)
\(\Leftrightarrow\left(x-7\sqrt{x}+6\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)\left(\sqrt{x}-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=36\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Giải phương trình:(Nhớ tìm điều kiện)a) sqrt{2x-1}sqrt{5}b)sqrt{x-5} 3c)sqrt{4x^2+4x+1}6d)sqrt{left(x-3right)^2}3-xe)sqrt{2x+5}sqrt{1-x}f)sqrt{x^2-x}sqrt{3-x}g)sqrt{2x^2-3}sqrt{4x-3}h)sqrt{2x-5}sqrt{x-3}i)sqrt{x^2-x+6}sqrt{x^2+3}
Đọc tiếp
Giải phương trình:(Nhớ tìm điều kiện)
a) \(\sqrt{2x-1}=\sqrt{5}\)
b)\(\sqrt{x-5}\) = 3
c)\(\sqrt{4x^2+4x+1}=6\)
d)\(\sqrt{\left(x-3\right)^2}=3-x\)
e)\(\sqrt{2x+5}=\sqrt{1-x}\)
f)\(\sqrt{x^2-x}=\sqrt{3-x}\)
g)\(\sqrt{2x^2-3}=\sqrt{4x-3}\)
h)\(\sqrt{2x-5}=\sqrt{x-3}\)
i)\(\sqrt{x^2-x+6}=\sqrt{x^2+3}\)
a, ĐKXĐ : \(x\ge\dfrac{1}{2}\)
PT <=> 2x - 1 = 5
<=> x = 3 ( TM )
Vậy ...
b, ĐKXĐ : \(x\ge5\)
PT <=> x - 5 = 9
<=> x = 14 ( TM )
Vậy ...
c, PT <=> \(\left|2x+1\right|=6\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=6\\2x+1=-6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)
Vậy ...
d, PT<=> \(\left|x-3\right|=3-x\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=x-3\\x-3=3-x\end{matrix}\right.\)
Vậy phương trình có vô số nghiệm với mọi x \(x\le3\)
e, ĐKXĐ : \(-\dfrac{5}{2}\le x\le1\)
PT <=> 2x + 5 = 1 - x
<=> 3x = -4
<=> \(x=-\dfrac{4}{3}\left(TM\right)\)
Vậy ...
f ĐKXĐ : \(\left[{}\begin{matrix}x\le0\\1\le x\le3\end{matrix}\right.\)
PT <=> \(x^2-x=3-x\)
\(\Leftrightarrow x=\pm\sqrt{3}\) ( TM )
Vậy ...
Đúng 3
Bình luận (0)
a) \(\sqrt{2x-1}=\sqrt{5}\) (x \(\ge\dfrac{1}{2}\))
<=> 2x - 1 = 5
<=> x = 3 (tmđk)
Vậy S = \(\left\{3\right\}\)
b) \(\sqrt{x-5}=3\) (x\(\ge5\))
<=> x - 5 = 9
<=> x = 4 (ko tmđk)
Vậy x \(\in\varnothing\)
c) \(\sqrt{4x^2+4x+1}=6\) (x \(\in R\))
<=> \(\sqrt{\left(2x+1\right)^2}=6\)
<=> |2x + 1| = 6
<=> \(\left[{}\begin{matrix}\text{2x + 1=6}\\\text{2x + 1}=-6\end{matrix}\right.< =>\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=\dfrac{-7}{2}\end{matrix}\right.\)(tmđk)
Vậy S = \(\left\{\dfrac{5}{2};\dfrac{-7}{2}\right\}\)
Đúng 1
Bình luận (0)
B1: rút gọn:a, sqrt{4-2sqrt{3}}-sqrt{3}b, sqrt{11+6sqrt[]{2}}-3+sqrt{2} c, x-4+sqrt{16-8x+x^2} với x 4d, dfrac{x^2-5}{x+sqrt{5}} x khác -sqrt{5}e, dfrac{x^2+2sqrt{2}x+2}{x+sqrt{2}} x khác -sqrt{2}g, dfrac{sqrt{6}+sqrt{14}}{2sqrt{3}+sqrt{28}}giúp em với ạ , em cảm ơn
Đọc tiếp
B1: rút gọn:
a, \(\sqrt{4-2\sqrt{3}}-\sqrt{3}\)
b, \(\sqrt{11+6\sqrt[]{2}}-3+\sqrt{2}\)
c, \(x-4+\sqrt{16-8x+x^2}\) với x > 4
d, \(\dfrac{x^2-5}{x+\sqrt{5}}\) x khác \(-\sqrt{5}\)
e, \(\dfrac{x^2+2\sqrt{2}x+2}{x+\sqrt{2}}\) x khác \(-\sqrt{2}\)
g, \(\dfrac{\sqrt{6}+\sqrt{14}}{2\sqrt{3}+\sqrt{28}}\)
giúp em với ạ , em cảm ơn ![]()
a) \(\sqrt{4-2\sqrt{3}}-\sqrt{3}=\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{3}=\sqrt{3}-1-\sqrt{3}=-1\)
b) \(\sqrt{11+6\sqrt{2}}-3+\sqrt{2}=\sqrt{\left(3+\sqrt{2}\right)^2}-3+\sqrt{2}=3+\sqrt{2}-3+\sqrt{2}\)
\(=2\sqrt{2}\)
c) \(x-4+\sqrt{16-8x+x^2}=x-4+\sqrt{\left(x-4\right)^2}=x-4+\left|x-4\right|\)
\(=x-4+x-4\left(x>4\right)=2x-8\)
d) \(\dfrac{x^2-5}{x+\sqrt{5}}=\dfrac{\left(x-\sqrt{5}\right)\left(x+\sqrt{5}\right)}{x+\sqrt{5}}=x-\sqrt{5}\)
e) \(\dfrac{x^2+2\sqrt{2}x+2}{x+\sqrt{2}}=\dfrac{\left(x+\sqrt{2}\right)^2}{x+\sqrt{2}}=x+\sqrt{2}\)
g) \(\dfrac{\sqrt{6}+\sqrt{14}}{2\sqrt{3}+\sqrt{28}}=\dfrac{\sqrt{2}\left(\sqrt{3}+\sqrt{7}\right)}{2\left(\sqrt{3}+\sqrt{7}\right)}=\dfrac{1}{\sqrt{2}}\)
Đúng 1
Bình luận (1)
a) Ta có: \(\sqrt{4-2\sqrt{3}}-\sqrt{3}\)
\(=\sqrt{3}-1-\sqrt{3}\)
=-1
b) Ta có: \(\sqrt{11+6\sqrt{2}}-3+\sqrt{2}\)
\(=3+\sqrt{2}-3+\sqrt{2}\)
\(=2\sqrt{2}\)
c) Ta có: \(x-4+\sqrt{x^2-8x+16}\)
\(=x-4+x-4=2x-8\)
d) Ta có: \(\dfrac{x^2-5}{x+\sqrt{5}}\)
\(=\dfrac{\left(x+\sqrt{5}\right)\left(x-\sqrt{5}\right)}{x+\sqrt{5}}\)
\(=x-\sqrt{5}\)
Đúng 1
Bình luận (1)
1.\(\sqrt{-4x^2+25}=x\)
2.\(\sqrt{3x^2-4x+3}=1-2x\)
3. \(\sqrt{4\left(1-x\right)^2}-\sqrt{3}=0\)
4.\(\dfrac{3\sqrt{x+5}}{\sqrt{ }x-1}< 0\)
5. \(\dfrac{3\sqrt{x-5}}{\sqrt{x+1}}\ge0\)
Giải PT:
a) -5x+7\(\sqrt{x}\) +12=0
b) \(\dfrac{1}{3}\)\(\sqrt{4x^2-20}\) +2\(\sqrt{\dfrac{x^2-5}{9}}\) -3\(\sqrt{x^2-5}=0\)
c) \(\sqrt{9x+27}+5\sqrt{x+3}-\dfrac{3}{4}\sqrt{16x+48}=5\)
d) \(\sqrt{49x-98}-14\sqrt{\dfrac{x-2}{49}}=3\sqrt{x-2}+8\)
a. ĐKXĐ: $x\geq 0$
PT $\Leftrightarrow -5x-5\sqrt{x}+12\sqrt{x}+12=0$
$\Leftrightarrow -5\sqrt{x}(\sqrt{x}+1)+12(\sqrt{x}+1)=0$
$\Leftrightarrow (\sqrt{x}+1)(12-5\sqrt{x})=0$
Dễ thấy $\sqrt{x}+1>1$ với mọi $x\geq 0$ nên $12-5\sqrt{x}=0$
$\Leftrightarrow \sqrt{x}=\frac{12}{5}$
$\Leftrightarrow x=5,76$ (thỏa mãn)
Đúng 1
Bình luận (0)
d. ĐKXĐ: $x\geq 2$
PT $\Leftrightarrow \sqrt{49}.\sqrt{x-2}-14\sqrt{\frac{1}{49}}\sqrt{x-2}=3\sqrt{x-2}+8$
$\Leftrightarrow 7\sqrt{x-2}-2\sqrt{x-2}=3\sqrt{x-2}+8$
$\Leftrightarrow 2\sqrt{x-2}=8$
$\Leftrightarrow \sqrt{x-2}=4$
$\Leftrightarrow x=4^2+2=18$ (tm)
Đúng 0
Bình luận (0)
b. ĐKXĐ: $x^2\geq 5$
PT $\Leftrightarrow \frac{1}{3}\sqrt{4}.\sqrt{x^2-5}+2\sqrt{\frac{1}{9}}\sqrt{x^2-5}-3\sqrt{x^2-5}=0$
$\Leftrightarrow \frac{2}{3}\sqrt{x^2-5}+\frac{2}{3}\sqrt{x^2-5}-3\sqrt{x^2-5}=0$
$\Leftrightarrow -\frac{5}{3}\sqrt{x^2-5}=0$
$\Leftrightarrow \sqrt{x^2-5}=0$
$\Leftrightarrow x=\pm \sqrt{5}$
Đúng 0
Bình luận (0)
Xem thêm câu trả lời