Cmr : ( a^2 + b^2 ).( x^2 + y^2 ) = ( ax - by )^2 + ( ay + bx )^2

Những câu hỏi liên quan
CMR:\(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax-by\right)^2+\left(ay+bx\right)^2\)
Ta có:
\(\left(a^2+b^2\right)\left(x^2+y^2\right)=a^2x^2+a^2y^2+b^2x^2+b^2y^2\)
\(=a^2x^2-2abxy+b^2y^2+a^2y^2+2abxy+b^2x^2\) \(=\left(ax-by\right)^2+\left(ay+bx\right)\)
\(=vp\)
\(\Rightarrowđpcm\)
Đúng 0
Bình luận (0)
Cho \(\dfrac{bz+cy}{x\left(-ax+by+cz\right)}=\dfrac{cx+az}{y\left(ax-by+cz\right)}=\dfrac{ay+bx}{z\left(ax+by-cz\right)}\)
CMR : \(\dfrac{ay+bx}{c}=\dfrac{bz+cy}{a}=\dfrac{cx+az}{b}\)
b) \(\dfrac{x}{a\left(b^2+c^2-a^2\right)}=\dfrac{y}{b\left(a^2+c^2-b^2\right)}=\dfrac{z}{c\left(a^2+b^2-c^2\right)}\)
CMR ( \(\left(a^2+b^2\right).\left(x^2+y^2\right)=\left(ax-by\right)^2+\left(ay-bx\right)^2\)
Đặt thừa số chúng viết tổng thành tích
a) ax - by - ay + bx
b) ax + by - ay - bx
c) a2 - ( b+c) a + bc
d) ( 3a-2)(4a-3) -(2-3a)(3a+1)
e) ax + ay + az - bx - by - bz - x - y - z
Tính giá trị biểu thức
A= ax + ay + bx + by + x + y với x + y = -9/4 và a + b = 1/3
B= ax + ay - bx - by - x - y với x + y = 1/2 và a - b = 1/2
Ta có :
A= ax+ay+bx+by+x+y
= a(x+y)+b(x+y)+x+y
= (a+b+1)(x+y)
= (\(\dfrac{1}{3}\)+1).\(\dfrac{-9}{4}\)
= \(\dfrac{4}{3}.\dfrac{-9}{4}\)
= -3
Đúng 0
Bình luận (0)
B= ax+ay-bx-by-x-y
= a(x+y)-b(x+y)-(x+y)
= (a-b-1)(x+y)
= (\(\dfrac{1}{2}\)-1).\(\dfrac{1}{2}\)
= \(\dfrac{-1}{2}.\dfrac{1}{2}\)
= \(\dfrac{-1}{4}\)
Đúng 0
Bình luận (0)
Tính giá trị biêu thuc:
a/ ax+ay+bx+by biết a+b=-2,x+y=17
b/ax-ay+bx-by biết a+b=-7,x-y=-1
a) \(ax+ay+bx+by=a\left(x+y\right)+b\left(x+y\right)=\left(a+b\right)\left(x+y\right)=\left(-2\right).17=-34\)
b) \(ax-ay+bx-by=a\left(x-y\right)+b\left(x-y\right)=\left(a+y\right)\left(x-y\right)=\left(-7\right).\left(-1\right)=7\)
Tính giá trị biêu thuc:
a/ ax+ay+bx+by biết a+b=-2,x+y=17
b/ax-ay+bx-by biết a+b=-7,x-y=-1
nhjjfkjnkorkgbklklflfjkbknkm
A,=a.(x+y)+b.(x+y)
=(x+y).(a+B)
=17.(-2)
=-34
Tính giá trị của biểu thức:
a,ax+ay+bx+by biết a+b=-2;x+y=17
b,ax-ay+bx-by biết a+b=-7; x-y=-1
a) suy ra a.(x+y)+b.(x+y)
suy ra (x+y) (a+b)
suy ra 17. (-2) = 34
b) suy ra a.(x-y) + b.(x-y)
suy ra (a+b) (x-y)
suy ra (-7).(-1)
mk làm bậy ko bít đúng hay ko
Đúng 0
Bình luận (0)
bn nào viết rõ hơn giùm mik đc ko.
(a^2+b^2)(x^2+y^2)=(ax+by)^2
<=> a^2x^2 + a^2y^2 + b^2x^2 + b^2y^2 = a^2x^2 + 2abxy + b^2y^2
<=> a^2y^2 + b^2x^2 = 2abxy
<=> a^2y^2 + b^2x^2 - 2abxy = 0
<=> (ay - bx)^2 = 0
=> ay - bx = 0
=> ay = bx
=> a/x = b/y ( x,y khác 0)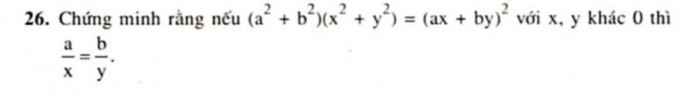
Ta có: \(\left(ax+by\right)^2=\left(a^2+b^2\right)\left(x^2+y^2\right)\)
\(\Leftrightarrow a^2x^2+2abxy+b^2y^2=a^2x^2+a^2y^2+x^2b^2+b^2y^2\)
\(\Leftrightarrow2abxy=a^2y^2+x^2b^2\)
\(\Leftrightarrow\left(ay-xb\right)^2=0\)
\(\Leftrightarrow ay=xb\)
hay \(\dfrac{a}{x}=\dfrac{b}{y}\)
Đúng 1
Bình luận (0)



















