cho f(x) = \(\dfrac{2\sqrt{x+1}-x-2}{x^2}\) (x≠0) và 2-9m (x=0) . tìm m để hàm số liên tục tại \(x_0\)=0
Những câu hỏi liên quan
Câu 1:Cho f(x) dfrac{sqrt{x+2}-sqrt{2-x}}{x}, x≠0. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu thì hàm số f(x) liên tục tại x0?Câu 2:Xét tính liên tục của hàm sốa, f(x) left{{}begin{matrix}x+dfrac{3}{2}dfrac{sqrt{x+1}-1}{sqrt[3]{1+x}-1}end{matrix}right.khi x≤0 và x0 tại xo0b, f(x) left{{}begin{matrix}dfrac{x^3-x^2+2x-2}{x-1}3x+aend{matrix}right.với x1 và với x≥1, xo1
Đọc tiếp
Câu 1:
Cho f(x)= \(\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}\), x≠0. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu thì hàm số f(x) liên tục tại x=0?
Câu 2:
Xét tính liên tục của hàm số
a, f(x)= \(\left\{{}\begin{matrix}x+\dfrac{3}{2}\\\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}\end{matrix}\right.\)khi x≤0 và x>0 tại xo=0
b, f(x)= \(\left\{{}\begin{matrix}\dfrac{x^3-x^2+2x-2}{x-1}\\3x+a\end{matrix}\right.\)với x<1 và với x≥1, xo=1
1.
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{2x}{x\left(\sqrt{x+2}+\sqrt{2-x}\right)}=\lim\limits_{x\rightarrow0}\dfrac{2}{\sqrt{x+2}+\sqrt{2-x}}=\dfrac{2}{2\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
Vậy cần bổ sung \(f\left(0\right)=\dfrac{\sqrt{2}}{2}\) để hàm liên tục tại \(x=0\)
2.
a. \(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(x+\dfrac{3}{2}\right)=\dfrac{3}{2}\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}=\lim\limits_{x\rightarrow0^+}\dfrac{x\left(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1\right)}{x\left(\sqrt[]{x+1}+1\right)}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1}{\sqrt[]{x+1}+1}=\dfrac{3}{2}\)
\(\Rightarrow f\left(0\right)=\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\) nên hàm liên tục tại \(x=0\)
Đúng 1
Bình luận (0)
2b.
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\dfrac{x^3-x^2+2x-2}{x-1}=\lim\limits_{x\rightarrow1^-}\dfrac{x^2\left(x-1\right)+2\left(x-1\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1^-}\dfrac{\left(x^2+2\right)\left(x-1\right)}{x-1}=\lim\limits_{x\rightarrow1^-}\left(x^2+2\right)=3\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=f\left(1\right)=\lim\limits_{x\rightarrow1^+}\left(3x+a\right)=a+3\)
- Nếu \(a=0\Rightarrow f\left(1\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^+}f\left(x\right)\) hàm liên tục tại \(x=1\)
- Nếu \(a\ne0\Rightarrow\lim\limits_{x\rightarrow1^-}f\left(x\right)\ne\lim\limits_{x\rightarrow1^+}f\left(x\right)\Rightarrow\) hàm không liên tục tại \(x=1\)
Đúng 1
Bình luận (0)
2 tháng 3 2021 lúc 19:42
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{x+4}-2}{x}\left(x>0\right)\\mx^2+2m+\dfrac{1}{4}\left(x\le0\right)\end{matrix}\right.\) (m là tham số). tìm m để hàm số liên tục tại x=0
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt{x+4}-2}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{x}{x\left(\sqrt{x+4}+2\right)}=\lim\limits_{x\rightarrow0^+}\dfrac{1}{\sqrt{x+4}+2}=\dfrac{1}{4}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(mx^2+2m+\dfrac{1}{4}\right)=2m+\dfrac{1}{4}\)
Hàm liên tục tại x=0 khi: \(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Leftrightarrow2m+\dfrac{1}{4}=\dfrac{1}{4}\Leftrightarrow m=0\)
Đúng 1
Bình luận (1)
Tìm m để các hàm số f(x) = \(\left\{{}\begin{matrix}\dfrac{\sqrt{x+1}-1}{2x}khix>0\\2x^2+3mx+1khix\le0\end{matrix}\right.\) liên tục tại x=0
Lời giải:
Để hàm liên tục tại $x=0$ thì:
\(\lim\limits_{x\to 0+}f(x)=\lim\limits_{x\to 0-}f(x)=f(0)\)
\(\Leftrightarrow \lim\limits_{x\to 0+}\frac{\sqrt{x+1}-1}{2x}=\lim\limits_{x\to 0-}(2x^2+3mx+1)=1\)
\(\Leftrightarrow \lim\limits_{x\to 0+}\frac{1}{2(\sqrt{x+1}+1)}=0\Leftrightarrow \frac{1}{2}=0\) (vô lý)
Vậy không tồn tại $m$ thỏa mãn.
Đúng 0
Bình luận (0)
Tìm a để các hàm số sau liên tục tại x0
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{1-x}+\sqrt{1+x}}{x}khix< 0\\a+\dfrac{4-x}{x+2}khi\ge0\end{matrix}\right.\)tại x0 = 0
Lời giải:
Để hàm số trên liên tục tại $x_0=0$ thì:
\(\lim\limits_{x\to 0+}f(x)=\lim\limits_{x\to 0-}f(x)=f(0)\)
\(\Leftrightarrow \lim\limits_{x\to 0+}(a+\frac{4-x}{x+2})=\lim\limits_{x\to 0-}(\frac{\sqrt{1-x}+\sqrt{1+x}}{x})=a+2\)
\(\Leftrightarrow a+2=\lim\limits_{x\to 0-}\frac{\sqrt{1-x}+\sqrt{1+x}}{x}\)
Mà \(\lim\limits_{x\to 0-}\frac{\sqrt{1-x}+\sqrt{1+x}}{x}=-\infty \) nên không tồn tại $a$ để hàm số liên tục tại $x_0=0$
Đúng 1
Bình luận (0)
Cho hàm số
f
(
x
)
3
-
9
-
x
x
,
0
x
9...
Đọc tiếp
Cho hàm số f ( x ) = 3 - 9 - x x , 0 < x < 9 m , x = 0 3 x , x ≥ 9 . Tìm m để f(x) liên tục trên [ 0 ; + ∞ )
A. 1 3
B. 1 2
C. 1 6
D. 1
19 tháng 2 2021 lúc 20:18
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt[3]{x+1}-1}{x}\left(x\ne0\right)\\2x+m+1\left(x=0\right)\end{matrix}\right.\)
tìm m để hàm số liên tục tại x=0
\(f\left(0\right)=2.0+m+1=m+1\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[3]{x+1}-1}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{x+1-1}{x(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1)}=\dfrac{1}{1+1+1}=\dfrac{1}{3}\)\(f\left(0\right)=\lim\limits_{x\rightarrow0^+}f\left(x\right)\Leftrightarrow m+1=\dfrac{1}{3}\Rightarrow m=-\dfrac{2}{3}\)
Đúng 2
Bình luận (0)
\(f(x) = \begin{cases} \dfrac{x^2-6x+8}{\sqrt{3x+2}-2} \ khi \ x < 2 \\ \dfrac{x+8}{x-1} \ khi \ x \geq 2 \\\end{cases}
tại x_0 =2.\) Xét tính liên tục của hàm số:
\(\lim\limits_{x->2^-}=\dfrac{2^2-6\cdot2+8}{\sqrt{3\cdot2+2}-2}=0\)
\(\lim\limits_{x->2^+}=\dfrac{2+8}{2-1}=10< >0\)
=>f(x) không liên tục tại x=2
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
3
-
9
-
x
x
,
0
x...
Đọc tiếp
Cho hàm số f ( x ) = 3 - 9 - x x , 0 < x < 9 m , x = 0 3 x , x ≥ 9 Tìm m để f(x) liên tục trên [0; +∞) là.
A. 1/3.
B. 1/2.
C. 1/6.
D. 1.
Chọn C.
TXĐ: D = [0; +∞).
Với x = 0 ta có f(0) = m.
Ta có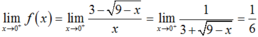 
.
Vậy để hàm số liên tục trên [0; +∞) khi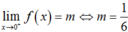 
.
Đúng 0
Bình luận (0)
16 tháng 11 2023 lúc 20:53
1/ Xét tính liên tục của hàm số tại một điểm:a) fleft(xright)left{{}begin{matrix}dfrac{x^2-4}{x^2+x-2};xne22x+1;x2end{matrix}right. tại x_02b) fleft(xright)left{{}begin{matrix}left(x+3right)^3-27;x0x^3+27;xle0end{matrix}right. tại x_00c) fleft(xright)left{{}begin{matrix}dfrac{x^3-6x^2-x+6}{x-1};x13x+5;xle1end{matrix}right. tại x_01d) fleft(xright)left{{}begin{matrix}dfrac{sqrt{3x+10}-x-4}{x+2};xne-2-dfrac{1}{4};x-2end{matrix}right. tại x_0-22/ Tìm m để hàm số sau liên tục tại điểm đã chỉ ra:a) ...
Đọc tiếp
1/ Xét tính liên tục của hàm số tại một điểm:
a) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-4}{x^2+x-2};x\ne2\\2x+1;x=2\end{matrix}\right.\) tại \(x_0=2\)
b) \(f\left(x\right)=\left\{{}\begin{matrix}\left(x+3\right)^3-27;x>0\\x^3+27;x\le0\end{matrix}\right.\) tại \(x_0=0\)
c) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^3-6x^2-x+6}{x-1};x>1\\3x+5;x\le1\end{matrix}\right.\) tại \(x_0=1\)
d) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{3x+10}-x-4}{x+2};x\ne-2\\-\dfrac{1}{4};x=-2\end{matrix}\right.\) tại \(x_0=-2\)
2/ Tìm \(m\) để hàm số sau liên tục tại điểm đã chỉ ra:
a) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-3x+2}{\sqrt{x+3}-2};x\ne1\\mx+2;x=1\end{matrix}\right.\) tại \(x_0=1\)
b) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt[3]{2x^2=9}-3}{2x-6};x\ne3\\m;x=3\end{matrix}\right.\) tại \(x_0=3\)
