giúp mình câu b ạ, cả câu c thì càng tốt

Những câu hỏi liên quan
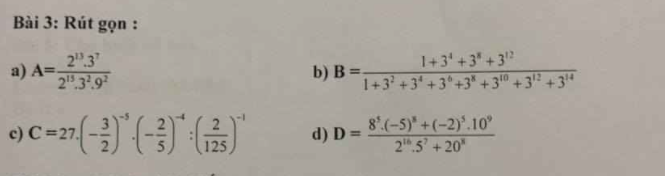 giúp mình với ạ cả 4 câu càng nhanh càng tốt
giúp mình với ạ cả 4 câu càng nhanh càng tốt
\(A=\dfrac{2^{13}\cdot3^7}{2^{15}\cdot3^2\cdot9^2}=\dfrac{2^{13}\cdot3^7}{2^{15}\cdot3^6}=\dfrac{3}{4}\)
\(C=27\cdot\left(-\dfrac{3}{2}\right)^{-5}\cdot\left(-\dfrac{2}{5}\right)^{-4}:\left(\dfrac{2}{125}\right)^{-1}\)
\(=27\cdot\dfrac{-32}{243}\cdot\dfrac{625}{16}\cdot\dfrac{2}{125}\)
\(=\dfrac{-32}{9}\cdot\dfrac{1}{8}\cdot5\)
\(=-\dfrac{20}{9}\)
Đúng 2
Bình luận (0)
Giải tự luận giúp em 1209 hoặc cả 2 câu thì càng tốt ạ
1209.
d nhận \(\overrightarrow{u}=\left(1;1;-1\right)\) là 1 vtcp
(P) nhận \(\overrightarrow{n}=\left(1;2;1\right)\) là 1 vtpt
Ta có: \(\overrightarrow{u_1}=\left[\overrightarrow{u};\overrightarrow{n}\right]=\left(3;-2;1\right)\)
\(\overrightarrow{u_2}=\left[\overrightarrow{u_1};\overrightarrow{n}\right]=\left(-4;-2;8\right)=-2\left(2;1;-4\right)\)
Phương trình d dạng tham số: \(\left\{{}\begin{matrix}x=t\\y=1+t\\z=2-t\end{matrix}\right.\)
Gọi M là giao điểm d và (P), tọa độ M thỏa mãn:
\(t+2\left(1+t\right)+2-t-4=0\Rightarrow t=0\Rightarrow M\left(0;1;2\right)\)
Do đó hình chiếu của d lên (P) nhận (2;1;-4) là 1 vtcp và đi qua M(0;1;2)
Phương trình: \(\dfrac{x}{2}=\dfrac{y-1}{1}=\dfrac{z-2}{-4}\)
Câu 1210 hoàn toàn tương tự
Đúng 1
Bình luận (2)
Cách làm nói chung:
- Tìm vecto chỉ phương \(\overrightarrow{u}\) của đường d và vtpt \(\overrightarrow{n}\) của mặt (P)
- Tính tích có hướng \(\overrightarrow{u_1}=\left(\overrightarrow{u};\overrightarrow{n}\right)\)
- Tiếp tục tính tích có hướng \(\overrightarrow{u_2}=\left[\overrightarrow{u_1};\overrightarrow{n}\right]\)
- Tìm tọa độ giao điểm M của d và (P)
- Hình chiếu vuông góc của d lên (P) sẽ đi qua M và nhận \(\overrightarrow{u_2}\) (hoặc 1 vecto cùng phương với nó) là 1 vtcp
Lưu ý rằng có vô số cách viết 1 pt đường thẳng (tùy thuộc cách chọn điểm) nên có thể trong 4 đáp án của đề bài không đáp án nào giống pt vừa viết được. Lúc đó cần kiểm tra bằng cách: 1. Loại những đáp án không giống vecto chỉ phương. 2. Trong những đáp án còn lại, tìm 1 điểm trên đó và thay vào pt đường thẳng vừa viết được, nếu thỏa mãn thì đó là đáp án đúng.
Đúng 1
Bình luận (0)
Giải giúp mình ạ, làm được bao nhiêu câu cũng được ạ hết thì càng tốt ạ
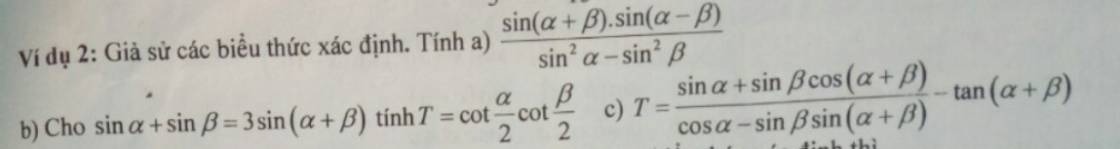
a: \(=\dfrac{-\dfrac{1}{2}\left[cos\left(a+b+a-b\right)-cos\left(a+b-a+b\right)\right]}{cos^2b-cos^2a}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left[cos2a-cos2b\right]}{\dfrac{1-cos2b}{2}-\dfrac{1-cos2a}{2}}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1-cos2b-1+cos2a}{2}}=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}=-1\)
c: \(T=\dfrac{sina+sinb\cdot\left(cosa\cdot cosb-sina\cdot sinb\right)}{cosa-sinb\cdot\left(sina\cdot cosb+sinb\cdot cosa\right)}-tan\left(a+b\right)\)
\(=\dfrac{sina+sinb\cdot cosa\cdot cosb-sin^2b\cdot sina}{cosa-sinb\cdot sina\cdot cosb-sin^2b\cdot cosa}-tan\left(a+b\right)\)
\(=\dfrac{sina\left(1-sin^2b\right)+sinb\cdot cosa\cdot cosb}{cosa\left(1-sin^2b\right)-sinb\cdot sina\cdot cosb}\)-tan(a+b)
\(=\dfrac{sina\cdot cos^2b+sinb\cdot cosa\cdot cosb}{cosa\cdot cos^2b-sinb\cdot sina\cdot cosb}-tan\left(a+b\right)\)
\(=\dfrac{sina\cdot cosb+sinb\cdot cosa}{cosa\cdot cosb-sina\cdot sinb}-tan\left(a+b\right)\)
\(=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}-tan\left(a+b\right)=0\)
Đúng 0
Bình luận (0)
 giúp mình với ạ càng nhanh càng tốt 4 câu trên ạ
giúp mình với ạ càng nhanh càng tốt 4 câu trên ạ
c: Ta có: \(\left(\dfrac{1}{2}\right)^{2x+1}=\dfrac{1}{8}\)
\(\Leftrightarrow2x+1=3\)
\(\Leftrightarrow2x=2\)
hay x=1
d: Ta có: \(\left(-\dfrac{1}{3}\right)^{x+3}=\dfrac{1}{81}\)
\(\Leftrightarrow x+3=4\)
hay x=1
Đúng 0
Bình luận (1)
Các bạn ơi,giúp mình với,mình bị bí hai câu này,đây là câu hỏi ôn thi nên mình mong mn sẽ giúp mình ạ,câu trả lời càng dài càng tốt ạ,cảm ơn mn nhiều

giải giúp mình câu 5 với ạ thêm mấy câu kia càng tốt
Bài 4
a, Số nu của gen là 90 x 20 = 1800 ( nu )
=> Chiều dài của gen \(\dfrac{1800}{2}.3,4=3060\left(A^O\right)\)
b,
Số nu của cả gen A=T=1800.20% = 360 (nu)
G=X=1800.30% = 540(nu)
Số nu từng mạch :
A1 = T2 = 15% . 900 = 135 ( nu )
T1 = A2 = 360 - 135 = 225 ( nu )
G1 = X2 = 540 - X1 = 540 - 360 = 180 ( nu )
X1 = G2 = 40% . 900 = 360 ( nu )
Đúng 1
Bình luận (0)
Bài 5
Ta có : \(\left\{{}\begin{matrix}H=2A+3G=N+G=3900\\G=900\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A=T=600\left(nu\right)\\G=X=900\left(nu\right)\\N=3000,N1=N2=1500\left(nu\right)\end{matrix}\right.\)
A1 = T2 = 30%.1500= 450 (nu)
T1 = A2 = 600 - 450 = 150 (nu)
G1 = X2 = 10%.1500 = 150 ( nu )
G2 = X1 = 900 - 150 = 750 (nu)
Đúng 1
Bình luận (0)

giúp mik câu 7 đến câu 15 lm được hết thì càng tốt ạ.
\(7,x^4+x^3+x^2-1=x^3\left(x+1\right)+\left(x-1\right)\left(x+1\right)=\left(x^3+x-1\right)\left(x+1\right)\)
\(8,x^2y^2+1-x^2-y^2=\left(x^2y^2-y^2\right)-\left(x^2-1\right)\\ =y^2\left(x^2-1\right)-\left(x^2-1\right)=\left(x-1\right)\left(x+1\right)\left(y-1\right)\left(y+1\right)\)
\(10,x^4-x^2+2x-1=x^4-\left(x-1\right)^2=\left(x^2-x+1\right)\left(x^2+x-1\right)\\ 11,3a-3b+a^2-2ab+b^2=3\left(a-b\right)+\left(a-b\right)^2=\left(3+a-b\right)\left(a-b\right)\\ 12,a^2+2ab+b^2-2a-2b+1=\left(a+b\right)^2-2\left(a+b\right)+1=\left(a+b-1\right)^2\\ 13,a^2-b^2-4a+4b=\left(a-b\right)\left(a+b\right)-4\left(a-b\right)=\left(a+b-4\right)\left(a-b\right)\\ 14,a^3-b^3-3a+3b=\left(a-b\right)\left(a^2+ab+b^2\right)-3\left(a-b\right)=\left(a-b\right)\left(a^2+ab+b^2-3\right)\\ 15,x^3+3x^2-3x-1=\left(x-1\right)\left(x^2+x+1\right)+3x\left(x-1\right)=\left(x-1\right)\left(x^2+4x+1\right)\)
Đúng 2
Bình luận (0)
1)
=0,25y.(64x3+z3)
2)
=x2(x2-4x+4)
=x2(x-2)2
5)
=x2(x+1)-4(x+1)
=(x2-4)(x+1)
=(x-2)(x+2)(x+1)
6)
=x2(x-1)-(x-1)
=(x2-1)(x-1)
=(x-1)(x+1)(x-1)
=(x-1)2(x+1)
Đúng 0
Bình luận (0)
nhờ mọi người chữa đề giúp mình ạ. Câu nào sai thì mong sửa lại+ trình bày cách giải (chi tiết càng tốt)


7.
Phương trình đường tròn \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) với tâm \(I=\left(a;b\right)\), bán kính \(R\)
\(\Rightarrow\) Tâm đường tròn \(\left(x-1\right)^2+\left(y+2\right)^2=4\) có tọa độ \(\left(1;-2\right)\)
Kết luận: Tâm đường tròn có tọa độ \(\left(1;-2\right)\).
Đúng 2
Bình luận (0)
9.
Cos đối, sin bù, phụ chéo, khác \(\pi\) tan, kém \(\dfrac{\pi}{2}\) chéo sin
\(sin\left(x+\dfrac{\pi}{2}\right)=sin\left(\dfrac{\pi}{2}-\left(-x\right)\right)=cos\left(-x\right)=cosx\)
Kết luận: \(sin\left(x+\dfrac{\pi}{2}\right)=cosx\)
Đúng 2
Bình luận (0)
14.
\(\dfrac{1-2x}{x+1}\ge-1\)
\(\Leftrightarrow\dfrac{1-2x}{x+1}+1\ge0\)
\(\Leftrightarrow\dfrac{2-x}{x+1}\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2-x\ge0\\x+1>0\end{matrix}\right.\\\left\{{}\begin{matrix}2-x\le0\\x+1< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-1< x\le2\\\left\{{}\begin{matrix}x\ge2\\x< -1\end{matrix}\right.\left(vn\right)\end{matrix}\right.\)
\(\Leftrightarrow-1< x\le2\)
\(\Leftrightarrow x\in(-1;2]\)
Kết luận: \(x\in(-1;2]\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Các bạn giúp mình câu b;c;d;e ạ. Các bạn làm được câu nào thì làm ạ, còn bạn nào giỏi giúp mình nhiều hơn thì tốt ạ! 
a: Chọn mp(SAC) có chứa AN
Gọi O là giao điểm của AC và BD
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
O∈AC⊂(SAC)
O∈BD⊂(SBD)
Do đó: O∈(SAC) giao (SBD)(1)
S∈(SAC)
S∈(SBD)
Do đó: S∈(SAC) giao (SBD)(2)
Từ (1),(2) suy ra (SAC) giao (SBD)=SO
Gọi I là giao điểm của SO và AN
=>I là giao điểm của AN và mp(SBD)
Xét ΔSAC có
SO,AN là các đường trung tuyến
SO cắt AN tại I
Do đó: I là trọng tâm của ΔSAC
=>\(\frac{IN}{IA}=\frac12\)
b: Chọn mp(ANB) có chứa NM
I∈AN⊂(ANB)
I∈SO⊂(SBD)
Do đó: I∈(ANB) giao (SBD)(3)
B∈(ANB)
B∈(SBD)
Do đó: B∈(ANB) giao (SBD)(4)
Từ (3),(4) suy ra (ANB) giao (SBD)=BI
Gọi K là giao điểm của MN và BI
=>K là giao điểm của MN và (SBD)
c: Vì K là giao điểm của MN và BI
nên B,K,I thẳng hàng
Đúng 0
Bình luận (0)



















