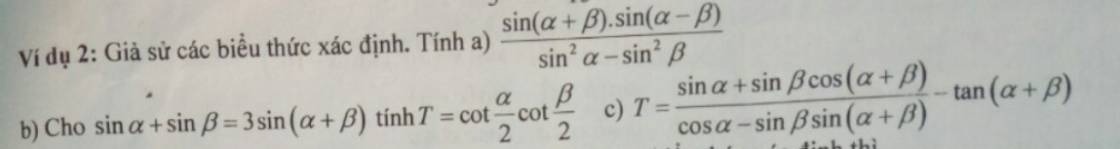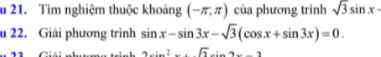a: \(=\dfrac{-\dfrac{1}{2}\left[cos\left(a+b+a-b\right)-cos\left(a+b-a+b\right)\right]}{cos^2b-cos^2a}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left[cos2a-cos2b\right]}{\dfrac{1-cos2b}{2}-\dfrac{1-cos2a}{2}}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1-cos2b-1+cos2a}{2}}=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}=-1\)
c: \(T=\dfrac{sina+sinb\cdot\left(cosa\cdot cosb-sina\cdot sinb\right)}{cosa-sinb\cdot\left(sina\cdot cosb+sinb\cdot cosa\right)}-tan\left(a+b\right)\)
\(=\dfrac{sina+sinb\cdot cosa\cdot cosb-sin^2b\cdot sina}{cosa-sinb\cdot sina\cdot cosb-sin^2b\cdot cosa}-tan\left(a+b\right)\)
\(=\dfrac{sina\left(1-sin^2b\right)+sinb\cdot cosa\cdot cosb}{cosa\left(1-sin^2b\right)-sinb\cdot sina\cdot cosb}\)-tan(a+b)
\(=\dfrac{sina\cdot cos^2b+sinb\cdot cosa\cdot cosb}{cosa\cdot cos^2b-sinb\cdot sina\cdot cosb}-tan\left(a+b\right)\)
\(=\dfrac{sina\cdot cosb+sinb\cdot cosa}{cosa\cdot cosb-sina\cdot sinb}-tan\left(a+b\right)\)
\(=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}-tan\left(a+b\right)=0\)