a: Chọn mp(SAC) có chứa AN
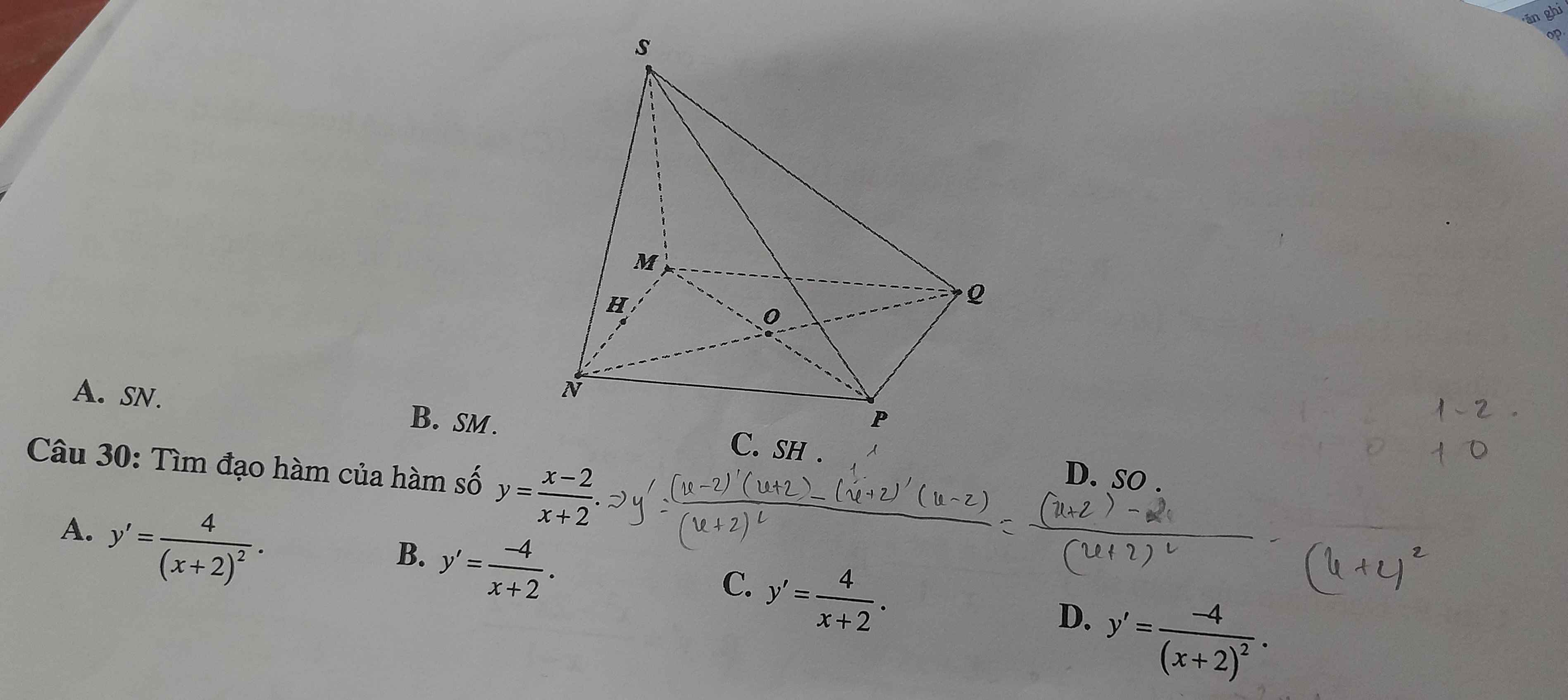
Gọi O là giao điểm của AC và BD
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
O∈AC⊂(SAC)
O∈BD⊂(SBD)
Do đó: O∈(SAC) giao (SBD)(1)
S∈(SAC)
S∈(SBD)
Do đó: S∈(SAC) giao (SBD)(2)
Từ (1),(2) suy ra (SAC) giao (SBD)=SO
Gọi I là giao điểm của SO và AN
=>I là giao điểm của AN và mp(SBD)
Xét ΔSAC có
SO,AN là các đường trung tuyến
SO cắt AN tại I
Do đó: I là trọng tâm của ΔSAC
=>\(\frac{IN}{IA}=\frac12\)
b: Chọn mp(ANB) có chứa NM
I∈AN⊂(ANB)
I∈SO⊂(SBD)
Do đó: I∈(ANB) giao (SBD)(3)
B∈(ANB)
B∈(SBD)
Do đó: B∈(ANB) giao (SBD)(4)
Từ (3),(4) suy ra (ANB) giao (SBD)=BI
Gọi K là giao điểm của MN và BI
=>K là giao điểm của MN và (SBD)
c: Vì K là giao điểm của MN và BI
nên B,K,I thẳng hàng