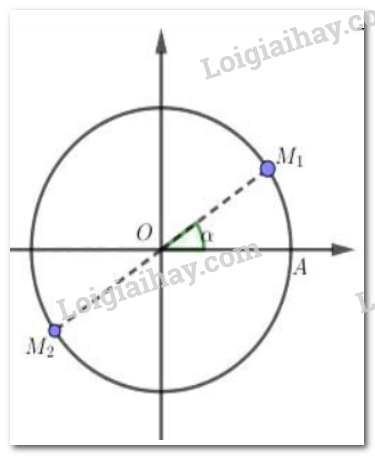
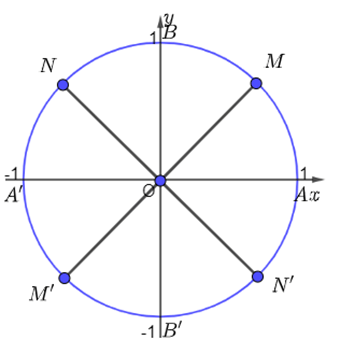
Tìm điểm biểu diễn trên đường tròn lượng giác của góc α = \(\dfrac{\pi}{2}+k\pi\left(k\in Z\right)\)

Những câu hỏi liên quan
Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng:
a) \(\frac{\pi }{4} + k\pi \,\,\left( {k \in Z} \right)\)
b) \(k\frac{\pi }{4}\,\,\left( {k \in Z} \right)\)
Cung có số đo \(\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\left(k\in Z\right)\) biểu diễn được bao nhiêu điểm trên đường tròn lượng giác
Trên đường tròn lượng giác góc A lấy điểm M sao cho số đo lượng giác \(\stackrel\frown{AM}\)=\(\alpha\) . Có bao nhiêu điểm M biết \(\alpha=\dfrac{\pi}{6}+\dfrac{k\pi}{3}\left(k\in Z\right)?\)
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?frac{pi }{2} + kfrac{{2pi }}{3},,left( {k in mathbb{Z}} right);frac{{ - pi }}{6} + kfrac{{2pi }}{3},,left( {k in mathbb{Z}} right);frac{pi }{2} + kfrac{pi }{3},,left( {k in mathbb{Z}} right)
Đọc tiếp
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?
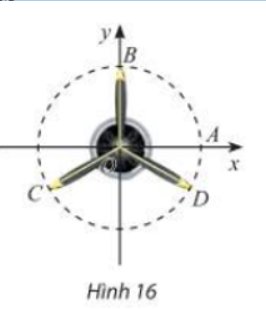
\(\frac{\pi }{2} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{\pi }{2} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
+ Xét góc lượng giác \(\frac{\pi }{2} + k\frac{{2\pi }}{3}\)
Với k = 0 thì \(\frac{\pi }{2} + 0.\frac{{2\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.
Với k = 1 thì \(\frac{\pi }{2} + 1.\frac{{2\pi }}{3} =\frac{7\pi }{6} \) được biểu diễn bởi điểm C.
Với k = 2 thì \(\frac{\pi }{2} + 2.\frac{{2\pi }}{3} =\frac{11\pi }{6} \) được biểu diễn bởi điểm D.
+ Xét góc lượng giác \(\frac{\pi }{2} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
Với k = 0 thì \(\frac{\pi }{2} + 0.\frac{{\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.
Với k = 1 thì \(\frac{\pi }{2} + 1.\frac{{\pi }}{3} =\frac{5\pi }{6} \) không biểu diễn bởi điểm nào.
+ Xét góc lượng giác \(\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
Với k = 1 thì \(\frac{{ - \pi }}{6}+ 1.\frac{{2\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.
Với k = 2 thì \(\frac{{ - \pi }}{6}+ 2.\frac{{2\pi }}{3} =\frac{7\pi }{6} \) được biểu diễn bởi điểm C.
Với k = 3 thì \(\frac{{ - \pi }}{6} + 3.\frac{{2\pi }}{3} =\frac{11\pi }{6} \) được biểu diễn bởi điểm D.
Vậy các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác
\(\frac{\pi }{2} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\,\,\left( {k \in \mathbb{Z}} \right)\)
Đúng 0
Bình luận (0)
Phương trình: \(\dfrac{Sin^42x+Cos^42x}{Tan\left(\dfrac{\pi}{4}-x\right)Tan\left(\dfrac{\pi}{4}+x\right)}=Cos^4x\) có bao nhiêu điểm biểu diễn nghiệm trên đường tròn lượng giác
\(\dfrac{sin^42x+cos^42x}{tan\left(\dfrac{\pi}{4}-x\right)tan\left(\dfrac{\pi}{4}+x\right)}=cos^4x\)
\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{cot\left(\dfrac{\pi}{4}+x\right)tan\left(\dfrac{\pi}{4}+x\right)}=cos^4x\)
\(\Leftrightarrow sin^42x+cos^42x=cos^4x\)
Giờ hạ bậc nữa là xong rồi. Làm nốt
Đúng 1
Bình luận (0)
Hình như đề bạn bị lỗi, thấy chỗ nào cũng ghi là \(cos^44x\).
ĐK: \(x\ne\dfrac{3\pi}{4}+k\pi;x\ne\dfrac{\pi}{4}+k\pi\)
\(\dfrac{sin^42x+cos^42x}{tan\left(\dfrac{\pi}{4}-x\right).tan\left(\dfrac{\pi}{4}+x\right)}=cos^44x\)
\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{\dfrac{sin\left(\dfrac{\pi}{4}-x\right)}{cos\left(\dfrac{\pi}{4}-x\right)}.\dfrac{sin\left(\dfrac{\pi}{4}+x\right)}{cos\left(\dfrac{\pi}{4}+x\right)}}=cos^44x\)
\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{\dfrac{cosx-sinx}{cosx+sinx}.\dfrac{cosx+sinx}{cosx-sinx}}=cos^44x\)
\(\Leftrightarrow sin^42x+cos^42x=cos^44x\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^24x=cos^44x\)
\(\Leftrightarrow cos^44x-\dfrac{1}{2}cos^24x-\dfrac{1}{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos^24x=1\\cos^24x=-\dfrac{1}{2}\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{1}{2}cos8x=\dfrac{1}{2}\)
\(\Leftrightarrow cos8x=1\)
\(\Leftrightarrow x=\dfrac{k\pi}{4}\)
Đối chiều điều kiện ban đầu ta được \(x=\dfrac{k\pi}{2}\)
Đúng 0
Bình luận (1)
Tính các giá trị lượng giác (nếu có) có mỗi góc sau:
a) \(\frac{\pi }{3} + k2\pi \,\,\left( {k \in Z} \right)\)
b) \(\frac{\pi }{3}+\left( 2k+1 \right)\pi \,\,\left( k\in \mathbb{Z} \right)\)
c) \(k\pi \,\,\left( {k \in Z} \right)\)
d) \(\frac{\pi }{2} + k\pi \,\,(k \in Z)\)
a)
\(\begin{array}{l}\cos \left( {\frac{\pi }{3} + k2\pi \,} \right) = \cos \left( {\frac{\pi }{3}} \right) = \frac{1}{2}\\\sin \left( {\frac{\pi }{3} + k2\pi \,} \right) = \sin \left( {\frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2}\\\tan \left( {\frac{\pi }{3} + k2\pi \,} \right) = \frac{{\sin \left( {\frac{\pi }{3} + k2\pi \,\,} \right)}}{{\cos \left( {\frac{\pi }{3} + k2\pi \,\,} \right)}} = \sqrt 3 \\\cot \left( {\frac{\pi }{3} + k2\pi \,\,} \right) = \frac{1}{{\tan \left( {\frac{\pi }{3} + k2\pi \,\,} \right)}} = \frac{{\sqrt 3 }}{3}\end{array}\)
b) Các giá trị lượng giác của góc lượng giác \(\frac{\pi }{3}+\left( 2k+1 \right)\pi \,\,\left( k\in \mathbb{Z} \right)\)
$ \cos \left[\frac{\pi}{3}+(2 \mathrm{k}+1) \pi\right]=\cos \left(\frac{\pi}{3}+\pi+2 \mathrm{k} \pi\right)=\cos \left(\frac{\pi}{3}+\pi\right)=-\cos \frac{\pi}{3}=-\frac{1}{2}$
$\sin \left[\frac{\pi}{3}+(2 \mathrm{k}+1) \pi\right]=\sin \left(\frac{\pi}{3}+\pi+2 \mathrm{k} \pi\right)=\sin \left(\frac{\pi}{3}+\pi\right)=-\sin \frac{\pi}{3}=-\frac{\sqrt{3}}{2}$
$\tan \left[\frac{\pi}{3}+(2 \mathrm{k}+1) \pi\right]=\tan \frac{\pi}{3}=\sqrt{3}$;
$\tan \left[\frac{\pi}{3}+(2 \mathrm{k}+1) \pi\right]=\cot \frac{\pi}{3}=\frac{\sqrt{3}}{3}$
c)
\(\begin{array}{l}\cos \left( {k\pi \,} \right) = \left[ \begin{array}{l} - 1\,\,\,\,\,\,\,\,\,\,\,\,\,;k = 2n + 1\\1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;k = 2n\,\,\,\end{array} \right.\\\sin \left( {k\pi \,} \right) = 0\\\tan \left( {k\pi \,} \right) = \frac{{\sin \left( {k\pi \,\,} \right)}}{{\cos \left( {k\pi \,\,} \right)}} = 0\\\cot \left( {k\pi \,\,} \right)\end{array}\)
d)
\(\begin{array}{l}\cos \left( {\frac{\pi }{2} + k\pi \,} \right) = 0\\\sin \left( {\frac{\pi }{2} + k\pi \,} \right) = \left[ \begin{array}{l}\sin \left( { - \frac{\pi }{2}} \right)\, = - 1\,\,\,\,\,\,\,;k = 2n + 1\\\sin \left( {\frac{\pi }{2}\,} \right)\, = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;k = 2n\,\,\,\end{array} \right.\\\tan \left( {\frac{\pi }{2} + k\pi \,} \right)\\\cot \left( {\frac{\pi }{2} + k\pi \,\,} \right) = 0\end{array}\)
Đúng 0
Bình luận (0)
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác
1, x=\(k\pi\)
2. \(\dfrac{k\pi}{2}\)
3, \(\left\{{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\\x\varepsilon\left[-2\pi;2\pi\right]\end{matrix}\right.\)
4,\(\left\{{}\begin{matrix}x=\dfrac{2\pi}{3}+k\pi\\x\varepsilon\left[-\pi;\pi\right]\end{matrix}\right.\)
Diễn tả giá trị lượng giác của góc sau bằng giá trị lượng giác của góc x
\(cos^{2015}\left(x-\dfrac{11\pi}{2}\right);cos^{2019}\left(x+\dfrac{7\pi}{2}\right);sin^{2019}\left(\dfrac{5\pi}{2}-x\right);cot^2\left(x-\dfrac{\pi}{2}\right)\)
Biểu diễn các góc lượng giác alpha - frac{{5pi }}{6},;beta frac{pi }{3},;gamma frac{{25pi }}{3},delta frac{{17pi }}{3} trên đường tròn lượng giác. Các góc nào có điểm biểu diễn trùng nhau? A. beta và gamma B. alpha, beta, gamma C. beta ,gamma ,delta D. alpha và beta ,
Đọc tiếp
Biểu diễn các góc lượng giác \(\alpha = - \frac{{5\pi }}{6},\;\beta = \frac{\pi }{3},\;\gamma = \frac{{25\pi }}{3},\delta = \frac{{17\pi }}{3}\) trên đường tròn lượng giác. Các góc nào có điểm biểu diễn trùng nhau?
A. \(\beta \) và \( \gamma \)
B. \(\alpha, \beta, \gamma \)
C. \(\beta ,\gamma ,\delta \)
D. \(\alpha \) và \(\beta \),
Ta có: \(\frac{{25\pi }}{3} = \frac{\pi }{3} + 4.2\pi .\) Do đó điểm biểu diễn cung lượng giác \(\frac{{25\pi }}{3}\) trùng với điểm biểu diễn cung lượng giác \(\frac{\pi }{3}\).
Vậy ta chọn đáp án A
Đúng 0
Bình luận (0)