Giải giúp mik bài này

Những câu hỏi liên quan
GIẢI HỘ MIK BÀI NÀY VỚI ĐIIIIIII . GIẢI GIÚP MIK BÀI NÀY NAH . Đ VÀ RÕ RÀNG NHÁ . ( ĐỌC TIẾP ) ĐI NHA

/ 2x - 3 / = 3 - 2x
Các bạn ơi giải giúp mik bài này vs ạ! Đáp án của bài này là S = {x ∈ R / x =< 3/2} mà mik ko biết cách giải ạ! Ai biết giúp mik vs! Thanks nhiều!
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
Đúng 1
Bình luận (0)
Giải giúp mik bài này nha ! Mik sẽ tick .
Bài 3:
a: Xét ΔCBA vuông tại B và ΔCHA vuông tại H có
CA chung
\(\widehat{BCA}=\widehat{HCA}\)
Do đó: ΔCBA=ΔCHA
Suy ra: CB=CH
hay ΔCBH cân tại C
b: Xét ΔBAF vuông tại B và ΔHAE vuông tại H có
AB=AH
\(\widehat{BAF}=\widehat{HAE}\)
Do đó: ΔBAF=ΔHAE
Suy ra: BF=HE
Xét ΔCFE có
CB/BF=CH/HE
nên BH//FE
c: Ta có: CF=CE
nên C nằm trên đường trung trực của EF(1)
Ta có: AF=AE
nên A nằm trên đường trung trực của FE(2)
Ta có: KF=KE
nên K nằm trên đường trung trực của FE(3)
Từ (1), (2) và (3) suy ra C,A,K thẳng hàng
Đúng 1
Bình luận (0)

giúp mik giải bài này vs![]()
![]() mik đag cần gấp
mik đag cần gấp
1: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)AC tại D
Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại F
2: Xét ΔFBH vuông tại F và ΔFAC vuông tại F có
\(\widehat{FBH}=\widehat{FAC}\left(=90^0-\widehat{ACF}\right)\)
Do đó: ΔFBH~ΔFAC
=>\(\dfrac{FB}{FA}=\dfrac{FH}{FC}\)
=>\(FB\cdot FC=FA\cdot FH\)
3: Xét tứ giác AEHD có
\(\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0\)
nên AEHD là tứ giác nội tiếp đường tròn đường kính AH
Tâm I là trung điểm của AH
Đúng 2
Bình luận (0)

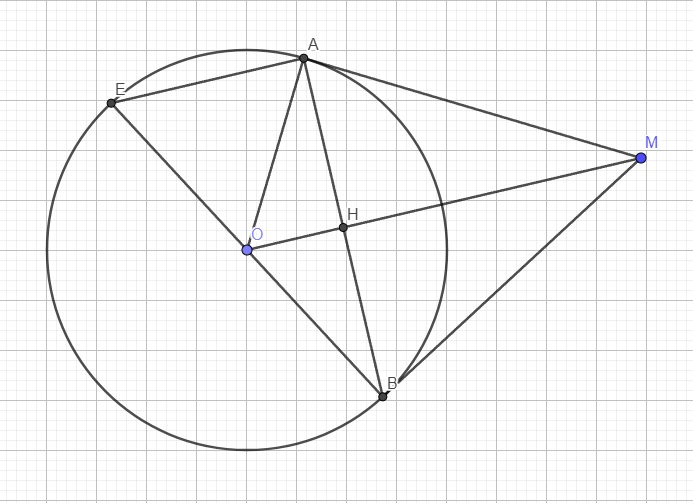
giúp mik giải bài này vs![]() mik đag cần gấp
mik đag cần gấp
a.
Do MA là tiếp tuyến tại A \(\Rightarrow MA\perp OA\Rightarrow\widehat{MAO}=90^0\)
Xét hai tam giác OMA và OMB có:
\(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\\OM\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OMA=\Delta OMB\left(c.c.c\right)\)
\(\Rightarrow\widehat{MBO}=\widehat{MAO}=90^0\)
\(\Rightarrow MB\perp OB\Rightarrow MB\) là tiếp tuyến
b.
Gọi H là giao điểm AB và OM
Ta có: \(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow OM\) là trung trực AB
\(\Rightarrow OM\perp AB\) tại H đồng thời \(HA=HB=\dfrac{AB}{2}\)
Trong tam giác vuông OMA: \(cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{2}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AOM}=60^0\)
\(\Rightarrow\widehat{AMO}=90^0-\widehat{AOM}=30^0\)
\(\Rightarrow\widehat{AMB}=2\widehat{AMO}=60^0\)
\(\Rightarrow\Delta AMB\) đều (tam giác cân có 1 góc bằng 60 độ)
Trong tam giác vuông OAH:
\(AH=OA.sin\widehat{AOM}=R.sin60^0=\dfrac{R\sqrt{3}}{3}\)
\(\Rightarrow AB=2AH=R\sqrt{3}\)
\(OH=OA.cos\widehat{AOM}=R.cos30^0=\dfrac{R}{2}\)
\(\Rightarrow HM=OM-OH=\dfrac{3R}{2}\)
\(\Rightarrow S_{ABM}=\dfrac{1}{2}HM.AB=\dfrac{3R^2\sqrt{3}}{4}\)
c.
BE là đường kính \(\Rightarrow\widehat{BAE}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAE}=90^0\Rightarrow AB\perp AE\)
Mà \(AB\perp OM\) (theo cm câu b)
\(\Rightarrow AE||OM\) (cùng vuông góc AB)
Đúng 1
Bình luận (1)
mik đang cần bài này gấp các bạn giải hết bài giúp mik nhé mik cần gấp để nộp bài cho thầy
e tách câu hỏi ra nhe tạm thời cj giúp mụt câu nhe
Đúng 1
Bình luận (0)
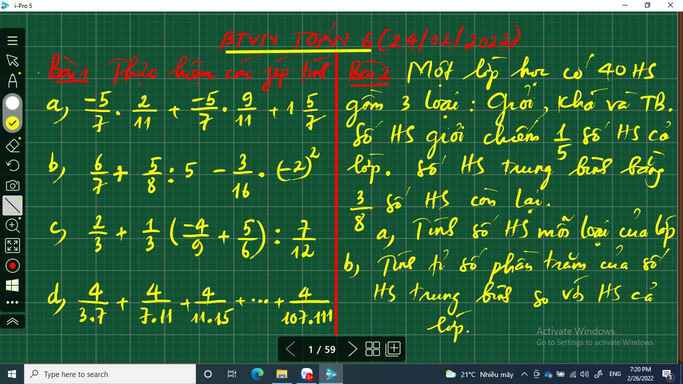
a: \(=\dfrac{-5}{7}\left(\dfrac{2}{11}+\dfrac{9}{11}\right)+1+\dfrac{5}{7}=\dfrac{-5}{7}+1+\dfrac{5}{7}=1\)
b: \(=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{3}{16}\cdot4=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{3}{4}=\dfrac{13}{56}\)
c: \(=\dfrac{2}{3}+\dfrac{1}{3}\cdot\dfrac{-24+45}{54}\cdot\dfrac{12}{7}\)
\(=\dfrac{2}{3}+\dfrac{1}{3}\cdot\dfrac{21}{54}\cdot\dfrac{12}{7}=\dfrac{2}{3}+\dfrac{2}{9}=\dfrac{6+2}{9}=\dfrac{8}{9}\)
d: \(=\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+...+\dfrac{1}{107}-\dfrac{1}{111}\)
\(=\dfrac{1}{3}-\dfrac{1}{111}=\dfrac{108}{333}=\dfrac{12}{37}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
giải giúp mik bài này ạ

\(x^4-4x^2+x^2-4x=0\)
\(\Leftrightarrow x^2\left(x^2-4\right)+x\left(x-4\right)=0\)
\(\Leftrightarrow x\left(x^3-4x+x-4\right)=0\)
\(\Leftrightarrow x\left(x^3-3x-4\right)=0\)
hay x=0
Đúng 1
Bình luận (0)
\(\Leftrightarrow x\left(x^3-3x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x^3-3x-4=0\end{matrix}\right.\\ \Leftrightarrow x=0\)
Đúng 1
Bình luận (0)
Giải giúp mik bài này vs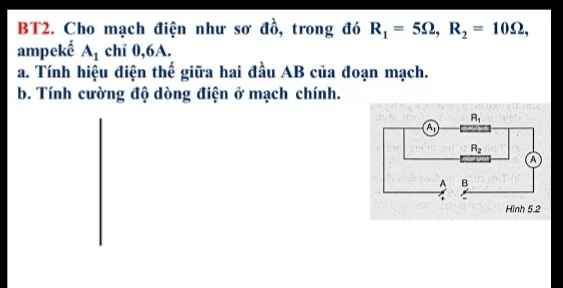
a, HĐT giữa 2 đầu R1:
Ta có: \(I_1=\dfrac{U_1}{R_1}\Leftrightarrow U_1=I_1R_1=0,6.5=3\left(V\right)\)
Mà UAB=U1=U2=3V
b, Điện trở tương đương:
\(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{5.10}{5+10}=3,33\left(\Omega\right)\)
CĐDĐ ở mạch chính:
\(I_{AB}=\dfrac{U_{AB}}{R_{tđ}}=\dfrac{3}{3,33}=0,9\left(A\right)\)
Đúng 1
Bình luận (0)
giải bài này giúp mik vs.