cho hàm số \(y=f\left(x\right)\) liên tục trên R thỏa 

\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\) ,                     \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=-\dfrac{1}{2}\)

tìm số đường tiệm cận củ đồ thị hàm số đã cho

\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\)

Xét các khẳng định sau

i) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại α ∈ - 1 ; 1 thỏa mãn   f ( x ) ≥ f ( α )   ∀ x ∈ - 1 ; 1 .

ii) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại β ∈ - 1 ; 1 thỏa mãn f ( x ) ≤ f ( β )   ∀ x ∈ - 1 ; 1 .

iii) Nếu hàm số y = f(x) xác định trên [-1;1] thỏa mãn f(-1).f(1)<0 thì tồn tại γ ∈ - 1 ; 1 thỏa mãn  f ( γ )   =   0

Số khẳng định đúng là

A. 3.

B. 2.

C. 1.

D. 0.

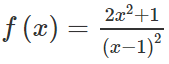
Cho hàm số y = f(x) thỏa mãn f ( 0 ) = 0 ;   f ' ( x ) = x x 2 + 1 . Họ nguyên hàm của hàm số g ( x ) = 4 xf ( x )   là:

A .   ( x 2 + 1 ) ln ( x 2 ) - x 2 + c

B .   x 2 ln ( x 2 + 1 ) - x 2

C .   ( x 2 + 1 ) ln ( x 2 + 1 ) - x 2 + c

D .   ( x 2 + 1 ) ln ( x 2 + 1 ) - x 2

Cho hàm số y=f(x) thỏa mãn f(-x)=f(x). Gọi đồ thị hàm số là (C). Chọn khẳng định đúng

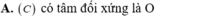
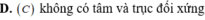
Cho hàm số y = f(x)

Biết hàm số đã cho thỏa mãn hệ thức ∫ f x sin x d x = - f x cos x + ∫ π 2 cosxdx . Hỏi hàm số y = f(x) là hàm số nào trong các hàm số sau?

A. .

B. .

C. .

D. .

1. Cho hs y=f(x) có đạo hàm thỏa mãn f'(6)=2. Tính giá trị biểu thức lim \(_{x->6}\)\(\dfrac{f\left(x\right)-f\left(6\right)}{x-6}\)

2. Gọi d là tiếp tuyến của hs y=\(\dfrac{x-1}{x+2}\) tại điểm có hoàng độ bằng -3. Khi đó d tạo với 2 trục tọa độ 1 tam giác có diện tích là bao nhiêu?

3. Cho lim \(_{x->2}\)\(\dfrac{\sqrt{3x+3}-m}{x-2}\)=\(\dfrac{a}{b}\)với m là số thực và \(\dfrac{a}{b}\)tối giản. Tính 2a-b

4. Cho hàm số y=f(x) xác định và có đạo hàm trên tập số thực. Biết f'(1)=5 và f(1)=6. Tìm giới hạn lim \(_{x->1}\)\(\dfrac{f^2\left(x\right)-f\left(x\right)-30}{\sqrt{x}-1}\)

5. Cho tam giác ABC có 2 trung tuyến kẻ từ A đến B vuông góc với nhau. Khi đó tỉ số \(\dfrac{AC+BC}{AB}\)đạt giá trị lớn nhất bằng bao nhiêu(làm tròn đến hàng phần trăm)

6. Cho tứ diện ABCD có (ACD) vuông góc (BCD), AC=AD=BC=BD=a và CD=2x. Gọi I và J lần lượt là trung điểm của AB và CD. Với giá trị nào của x thì (ABC) vuông góc với (ABD)?