Rút gọn các biểu thức:
a) A = ( k − 4 ) ( k 2 + 4 k + 16 ) − ( 128 + k 3 ) ;
b) B = ( 2 m + 3 n ) ( 4 m 2 − 6 mn + 9 n 2 ) − ( 3 m − 2 n ) ( 9 m 2 + 6 mn + 4 n 2 ) .
Bài 1: Rút gọn biểu thức:
a) A = \(\left(\frac{1}{x^2-4x}+\frac{2}{16-x^2}+\frac{4}{4x+16}\right):\frac{1}{4x}\)
\(A=\left(\dfrac{1}{x^2-4x}+\dfrac{2}{16-x^2}+\dfrac{4}{4x+16}\right):\dfrac{1}{4x}\left(x\ne4;x\ne-4;x\ne0\right).\)
\(A=\left(\dfrac{1}{x\left(x-4\right)}+\dfrac{-2}{\left(x+4\right)\left(x-4\right)}+\dfrac{1}{x+4}\right).4x\).
\(A=\dfrac{x+4-2x+x^2-4x}{x\left(x-4\right)\left(x+4\right)}.4x.\)
\(A=\dfrac{x^2-5x+4}{\left(x-4\right)\left(x+4\right)}.4.\)
\(A=\dfrac{\left(x-4\right)\left(x-1\right)}{\left(x-4\right)\left(x+4\right)}.4.\)
\(A=\dfrac{4\left(x-1\right)}{x+4}.\)
Bài 1. Rút gọn các biểu thức sau:
a) A=(k-4)(k2+4k+16)-(128+k3)
b) B=(2m+3n)(4m2-6mn+9n2)-(3m-2n)(9m2+6mn+4n2)
Bài 4.Tìm x biết
a) (x-1)3+(2-x)(4+2x+x2)+3x(x+2)=16
b) (x+2)(x2-2x+4)-x(x2-2)=15
Bài 1:
a: Ta có: \(A=\left(k-4\right)\left(k^2+4k+16\right)-\left(k^3+128\right)\)
\(=k^3-64-k^3-128\)
=-192
b: Ta có: \(B=\left(2m+3n\right)\left(4m^2-6mn+9n^2\right)-\left(3m-2n\right)\left(9m^2+6mn+4n^2\right)\)
\(=8m^3+27n^3-27m^3+8n^3\)
\(=-19m^3+35n^3\)
Bài 4:
a: Ta có: \(\left(x-1\right)^3+\left(2-x\right)\left(4+2x+x^2\right)+3x\left(x+2\right)=16\)
\(\Leftrightarrow x^3-3x^2+3x-1+8-x^3+3x^2+6x=16\)
\(\Leftrightarrow9x=9\)
hay x=1
b: ta có: \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x^2-2\right)=15\)
\(\Leftrightarrow x^3+8-x^3+2x=15\)
\(\Leftrightarrow2x=7\)
hay \(x=\dfrac{7}{2}\)
Câu 1. Khai triển các biểu thức:
a) (a-b+c)2 b) (a+2b-c)2
c) (2a-b-c)2
Câu 2. Rút gọn biểu thức:
a) A=(x-y)2+(x+y)2
b) B=(2x-1)2-2(2x-3)2+4
Câu 3. Tính nhanh:
a) 492 b) 512
c) 99.100
Câu 4. Tìm x, biết:
a) 16x2-(4x-5)2=15 b) (2x+1)(1-2x)+(1-2x)2=18
c) (x-5)2-x(x-4)=9 d) (x-5)2+(x-4)(1-x)=0
Tách ra mỗi câu một lần.
Dài quá không ai làm đâu.
Nhìn nản lắm.
Câu 3:
a: \(49^2=2401\)
b: \(51^2=2601\)
c: \(99\cdot100=9900\)
Cho biểu thức 2
1 2
1 1
K
a a
a) Tìm điều kiện của a để biểu thức K xác định. b) Rút gọn biểu thức K
c) Tính giá trị biểu thức K khi 1
2
\(a.a\ne\pm1\)
\(b.K=\dfrac{1}{a+1}+\dfrac{2}{a^2-1}=\dfrac{a-1}{\left(a-1\right)\left(a+1\right)}+\dfrac{2}{\left(a-1\right)\left(a+1\right)}=\dfrac{a+1}{\left(a-1\right)\left(a+1\right)}=\dfrac{1}{a-1}\)
\(c.K=\dfrac{1}{1-\dfrac{1}{2}}=\dfrac{1}{\dfrac{1}{2}}=2\)
Cho biểu thức: K=(\(\dfrac{x^2}{x^2-5x+6}\)+\(\dfrac{x^2}{x^2-3x+2}\)).\(\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+x^2+1}\)
a, Tìm đkxđ rồi rút gọn K
b, Tìm GTLN của K
a: ĐKXĐ: x<>1; x<>2; x<>3
\(K=\left(\dfrac{x^2}{\left(x-2\right)\left(x-3\right)}+\dfrac{x^2}{\left(x-1\right)\left(x-2\right)}\right)\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+2x^2+1-x^2}\)
\(=\dfrac{x^3-x^2+x^3-3x^2}{\left(x-2\right)\left(x-3\right)\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x^2+1+x\right)\left(x^2+1-x\right)}\)
\(=\dfrac{2x^3-4x^2}{\left(x-2\right)}\cdot\dfrac{1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^2\left(x-2\right)}{\left(x-2\right)\left(x^4+x^2+1\right)}=\dfrac{2x^2}{x^4+x^2+1}\)
b:
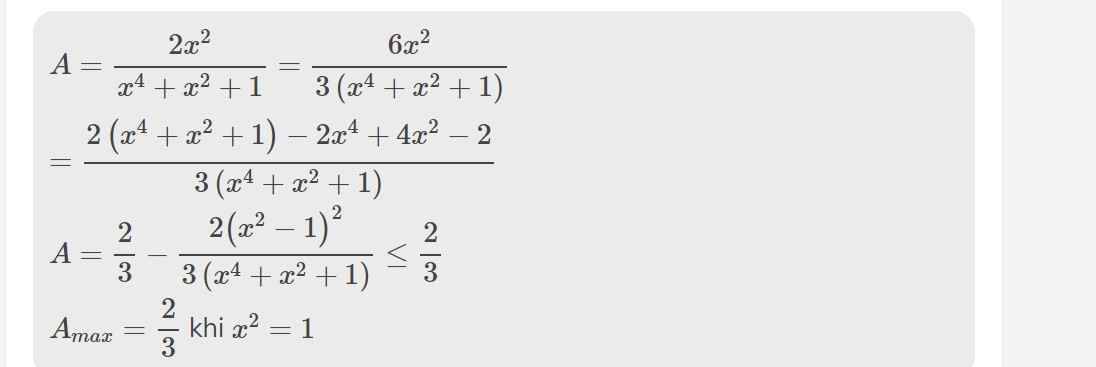
Rút gọn biểu thức:
a) A=(x-y)2+(x+y)2
b) B=(2x-1)2-2(2x-3)2+4
a, \(A=\left(x-y\right)^2+\left(x+y\right)^2\)
\(=x^2-2xy+y^2+x^2+2xy+y^2\)
\(=2x^2+2y^2\)
a) \(A=\left(x-y\right)^2+\left(x+y\right)^2\\ =x^2-2xy+y^2+x^2+2xy+y^2=2x^2+2y^2\)
b) \(B=\left(2x-1\right)^2-2\left(2x-3\right)^2+4\\ =4x^2-4x+1-2\left(4x^2-12x+9\right)+4\\ =4x^2-4x+1-8x^2+24x-18+4\)
\(=-4x^2+20x-13\)
Rút gọn biểu thức sau :
\(A=\frac{4+\sqrt{3}}{\sqrt{1}+\sqrt{3}}+\frac{6+\sqrt{8}}{\sqrt{3}+\sqrt{5}}+...+\frac{2k+\sqrt{k^2-1}}{\sqrt{k-1}+\sqrt{k+1}}+....+\frac{200+\sqrt{999}}{\sqrt{99}+\sqrt{100}}\)
Với mọi \(k\ge2\) thì \(\frac{2k+\sqrt{k^2-1}}{\sqrt{k-1}+\sqrt{k+1}}=\frac{\left[\left(\sqrt{k-1}\right)^2+\left(\sqrt{k+1}\right)^2+\sqrt{\left(k-1\right)\left(k+1\right)}\right]\left(\sqrt{k+1}-\sqrt{k-1}\right)}{\left(\sqrt{k-1}+\sqrt{k+1}\right)\left(\sqrt{k+1}-\sqrt{k-1}\right)}\)
\(=\frac{\sqrt{\left(k+1\right)^3}-\sqrt{\left(k-1\right)^3}}{2}\)
Suy ra tổng đã cho có thể viết là :
\(A=\frac{1}{2}\left[\sqrt{3^3}-\sqrt{1^3}+\sqrt{4^3}-\sqrt{2^3}+\sqrt{5^3}-\sqrt{3^3}+\sqrt{6^3}-\sqrt{4^3}+...+\sqrt{101^3}-\sqrt{99^3}\right]\)
\(=\frac{1}{2}\left[-1-\sqrt{2^3}+\sqrt{101^3}+\sqrt{100^3}\right]\)
\(=\frac{999+\sqrt{101^3}-\sqrt{8}}{2}\)
Rút gọn biểu thức:A=\(\dfrac{2}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}-2}+\dfrac{4}{x-4}\)
đk : x >= 0 ; x khác 4
\(A=\dfrac{2\sqrt{x}-4-\sqrt{x}-2+4}{x-4}=\dfrac{\sqrt{x}-2}{x-4}=\dfrac{1}{\sqrt{x}+2}\)
\(A=\dfrac{2}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}-2}+\dfrac{4}{x-4}\left(đk:x>2\right)\)
\(=\dfrac{2\left(\sqrt{x}-2\right)-\left(\sqrt{x}+2\right)+4}{x-4}\)
\(=\dfrac{2\sqrt{x}-4-\sqrt{x}-2+4}{x-4}=\dfrac{\sqrt{x}-2}{x-4}=\dfrac{1}{\sqrt{x}+2}\)
ĐKXĐ: x khác 4; x ≥ 0
\(A=\dfrac{2\sqrt{x}-4-\sqrt{x}-2+4}{x-4}=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{1}{\sqrt{x}+2}\)
Rút gọn các biểu thức
M = \(\sqrt{\left(3a-1\right)^2}+2a-3\) với a \(\ge\dfrac{1}{3}\)
N = \(\sqrt{\left(4-a\right)^2}-a+5\) với a > 4
I = \(\sqrt{\left(3-2a\right)^2}+2-7\) với a < \(\dfrac{3}{2}\)
K = \(\dfrac{a^2-9}{4}\sqrt{\dfrac{4}{\left(a-2\right)^2}}\) với a < 3
`M=sqrt{(3a-1)^2}+2a-3`
`=|3a-1|+2a-3`
`=3a-1+2a-3(do \ a>=1/3)`
`=5a-4`
`N=sqrt{(4-a)^2}-a+5`
`=|4-a|-a+5`
`=a-4-a+5(do \ a>4)`
`=1`
`I=sqrt{(3-2a)^2}+2-7`
`=|3-2a|-5`
`=3-2a-5(do \ a<3/2)`
`=-2-2a`
`K=(a^2-9)/4*sqrt{4/(a-2)^2}`
`=(a^2-9)/4*|2/(a-2)|`
`=(a^2-9)/(2|a-2|)`
Nếu `3>a>2=>|a-2|=a-2`
`=>K=(a^2-9)/(2(a-2))`
Nếu `a<2=>|a-2|=2-a`
`=>K=(a^2-9)/(2(2-a))`
\(M=\left|3a-1\right|+2a-3\)
Mà \(a-\dfrac{1}{3}\ge0\)
\(\Rightarrow M=3a-1+2a-3=5a-4\)
\(N=\left|4-a\right|-a+5\)
Mà \(4-a< 0\)
\(\Rightarrow N=a-4-a+5=1\)
\(I=\left|3-2a\right|-5\)
Mà \(a-\dfrac{3}{2}< 0\)
\(\Rightarrow I=3-2a-5=-2a-2\)
K, Ta có : \(a-3< 0\)
\(\Rightarrow K=\dfrac{2\left(a^2-9\right)}{4\left|a-2\right|}=\dfrac{\left(a-3\right)\left(a+3\right)}{\left|2a-4\right|}\)