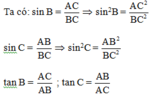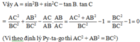Cho tam giác ABC có sin2A+sin2B=sin2C.Chứng minh rằng tam giác ABC vuông

Những câu hỏi liên quan
Chứng minh rằng trong tam giác ABC, ta có:
a. tanA + tanB + tanC = tanAtanBtanC 
b. sin2A + sin2B + sin2C = 4sinAsinBsinC
Vì A, B, C là ba góc của tam giác nên ta có : A + B + C = π.
⇒ C = π - (A + B); A + B = π - C
a) Ta có: tan A + tan B + tan C = (tan A + tan B) + tan C
= tan (A + B). (1 – tan A.tan B) + tan C
= tan (π – C).(1 – tan A. tan B) + tan C
= -tan C.(1 – tan A. tan B) + tan C
= -tan C + tan A. tan B. tan C + tan C
= tan A. tan B. tan C
b) sin 2A + sin 2B + sin 2C
= 2. sin (A + B). cos (A – B) + 2.sin C. cos C
= 2. sin (π – C). cos (A – B) + 2.sin C. cos (π – (A + B))
= 2.sin C. cos (A – B) - 2.sin C. cos (A + B)
= 2.sin C.[cos (A – B) - cos (A + B)]
= 2.sin C.[-2sinA. sin(- B)]
= 2.sin C. 2.sin A. sin B ( vì sin(- B)= - sinB )
= 4. sin A. sin B. sin C
Đúng 0
Bình luận (1)
Chứng minh đẳng thức sin2A+sin2B+sin2C=4sinA.sinB.sinC với A,B,C là 3 góc trong tam giác ABC
Lời giải:
Ta có:
$\sin 2A+\sin 2B=2\sin \frac{2A+2B}{2}\cos \frac{2A-2B}{2}=2\sin (A+B)\cos (A-B)$
$=2\sin (\pi -C)\cos (A-B)=2\sin C\cos (A-B) $
Do đó:
$\sin 2A+\sin 2B+\sin 2C=\sin 2C+2\sin C\cos (A-B)=2\sin C\cos C+2\sin C\cos (A-B)$
$=2\sin C[\cos C+\cos (A-B)]=2\sin C[\cos (\pi -A-B)+\cos (A-B)]$
$=2\sin C[\cos (A-B)-\cos (A+B)]=-2.\sin C[\cos (A+B)-\cos (A-B)]$
$=-2\sin C. (-2).\sin \frac{(A+B)+(A-B)}{2}.\sin \frac{(A+B)-(A-B)}{2}=4\sin C.\sin A.\sin B$
Ta có đpcm.
Cho tam giác ABC vuông tại A. Tính A = sin 2 B + sin 2 C - tan B . tan C
A. 0
B. 1
C. −1
D. 2
Cho tam giác ABC vuông tại A có AB = 6cm, BC = 10cm, đường cao AH. Gọi E, F là hình chiếu của H lần lượt lên AB, AC
a. Tính EF.
b. Chứng minh rằng: AE.AB = AF.AC
c. Tính: sin2B + sin2C – tanB.tanC
a) Xét tam giác ABC vuông tại A có:
\(BC^2=AB^2+AC^2\)(Định lý Pytago)
\(\Rightarrow AC^2=BC^2-AB^2=10^2-6^2=64\Rightarrow AC=8\left(cm\right)\)
Xét tam giác ABC vuông tại A có đường cao AH
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)(hệ thức lượng trong tam giác vuông)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}=\dfrac{25}{576}\Rightarrow AH=\dfrac{24}{5}\left(cm\right)\)
Xét tứ giác AEHF có:
\(\widehat{AEH}=\widehat{EAF}=\widehat{AFH}=90^0\)
=> Tứ giác AEHF là hình chữ nhật
=> \(EF=AH=\dfrac{24}{5}\left(cm\right)\)
b) Áp dụng tỉ số lượng giác của góc nhọn trong tam giác ABH và tam giác AHC vuông tại H:
\(AH^2=AE.AB\)
\(AH^2=AF.AC\)
\(\Rightarrow AE.AB=AF.AC\)
Đúng 1
Bình luận (2)
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=10^2-6^2=64\)
hay AC=8(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AB\cdot AC=AH\cdot BC\)
hay AH=4,8(cm)
Xét tứ giác AEHF có
\(\widehat{EAF}=\widehat{AFH}=\widehat{AEH}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=EF
hay FE=4,8(cm)
b: Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
Đúng 1
Bình luận (0)
Cho tam giác nhọn ABC, đường cao BE, CF. Gọi SAEF, SABC lần lượt là diện tích của tam giác AEF và tam giác ABC. Chứng minh SAEF/SABC =1-sin2A
Xét tam giác AEF và tam giác ABC có:
A chung
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\left(=cosA\right)\)
\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c.g.c\right)\)
\(\Rightarrow\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AE}{AB}\right)^2=cos^2A=1-sin^2A\)
Đúng 0
Bình luận (0)
\(1-\sin^2A=\cos^2A=\dfrac{AF^2}{AC^2}\left(1\right)\)
Ta có \(\widehat{AEB}=\widehat{AFC}=90^0\Rightarrow\Delta AEB\sim\Delta AFC\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AF}{AC}\Rightarrow\Delta AEF\sim\Delta ABC\left(c.g.c\right)\\ \Rightarrow\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AF}{AC}\right)^2=\dfrac{AF^2}{AC^2}\left(2\right)\\ \left(1\right)\left(2\right)\RightarrowĐpcm\)
Đúng 0
Bình luận (0)
Tìm số đo hóc của tam giác nếu có a.cosB-b.cosA=a.sinA-b.sinB và sin2A+sin2B+cos2A+cos2B= Căn 2
Các góc của tam giác ABC thỏa mãn hệ thức, \(\frac{sinB+sinC}{sinA}=\frac{sin2B+sin2C}{sin2A}\)
Chứng minh rằng cosB+cosC=1
Bài 1: Cho tam giác ABC cân tại A có các đường trung tuyến BE và CD . Chứng minh rằng BE bằng CD
Bài 2: Cho tam giác ABC có đường trung tuyến BE và CD, biết BE = CD . Chứng minh rằng tam giác ABC cân tại A
Bài 3: Cho tam giác ABC chứng minh rằng a) Nếu tam giác ABC vuông góc tại A , có trung tuyến AM =1/2 BC
b) Nếu trung tuyến AM =1/2 BC thì tam giác ABC vuông góc tại A
trong tam giác ABC ta có
sin2A + sin2B + sin2C = 4.sinA.sinB.sinC
\(sin2A+sin2B+sin2C=2sin\left(A+B\right).cos\left(A-B\right)+2sinC.cosC\)
\(=2sinC.cos\left(A-B\right)+2sinC.cosC=2sinC\left[cos\left(A-B\right)+cosC\right]\)
\(=4sinC.cos\left(\frac{A+C-B}{2}\right).cos\left(\frac{A-B-C}{2}\right)\)
\(=4sinC.cos\left(\frac{\pi-2B}{2}\right).cos\left(\frac{2A-\pi}{2}\right)=4sinC.cos\left(\frac{\pi-2B}{2}\right).cos\left(\frac{\pi-2A}{2}\right)\)
\(=4sinC.cos\left(\frac{\pi}{2}-B\right).cos\left(\frac{\pi}{2}-A\right)\)
\(=4sinA.sinB.sinC\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH . Gọi E,F lần lượt là hình chiếu của H AB và AC
a) Chứng minh AE.AB=AF.AC
b) Tính M,biết M=5.sin2C+5.sin2B+2tanB tanC
a: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF vuông góc AC
nên AF*AC=AH^2
=>AE*AB=AF*AC
b: M=5*sin^2C+5*cos^2C+2*tanB*cot B
=5+2
=7
Đúng 1
Bình luận (1)