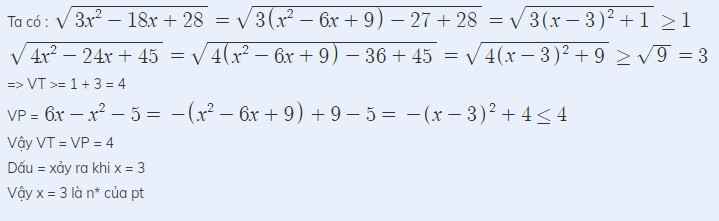h: \(\sqrt{18x}+\sqrt{32x}-14=0\)

\(\Leftrightarrow7\sqrt{2x}=14\)

hay x=2

b) Đặt \(\sqrt{x^2-6x+6}=a\left(a\ge0\right)\)

\(\Rightarrow a^2+3-4a=0\)

=> (a - 3).(a - 1) = 0

=> \(\left[{}\begin{matrix}a=3\\a=1\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}\sqrt{x^2-6x+6}=3\\\sqrt{x^2-6x+6}=1\end{matrix}\right.\)

Bình phương lên giải tiếp nhé!

c) Tương tư câu b nhé

a) \(\Leftrightarrow\sqrt{3}\left(x-1\right)+\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(\sqrt{3}-1\right)=0\Leftrightarrow x=1\)

b) \(\Leftrightarrow\sqrt{\left(x-3\right)^2}=7\)

\(\Leftrightarrow\left|x-3\right|=7\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=7\\x-3=-7\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=10\\x=-4\end{matrix}\right.\)

c) \(\Leftrightarrow3\left|x-2\right|=45\)

\(\Leftrightarrow\left|x-2\right|=15\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=15\\x-2=-15\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=17\\x=-13\end{matrix}\right.\)

\(a,PT\Leftrightarrow\sqrt{3}\left(x-1\right)=1-x\\ \Leftrightarrow\sqrt{3}\left(x-1\right)+\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(\sqrt{3}+1\right)=0\\ \Leftrightarrow x=1\left(\sqrt{3}+1\ne0\right)\\ b,ĐK:x\in R\\ PT\Leftrightarrow\left|x-3\right|=7\Leftrightarrow\left[{}\begin{matrix}x-3=7\\3-x=7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=10\\x=-4\end{matrix}\right.\\ c,ĐK:x\in R\\ PT\Leftrightarrow3\left|x-2\right|=45\Leftrightarrow\left|x-2\right|=15\\ \Leftrightarrow\left[{}\begin{matrix}x-2=15\\2-x=15\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=17\\x=-13\end{matrix}\right.\)

1: \(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+\sqrt{x-3}\right)=0\)

=>căn x-3=0

=>x-3=0

=>x=3

2: =>\(\sqrt{2x-3+2\sqrt{2x-3}+1}+\sqrt{2x-3+2\cdot\sqrt{2x-3}\cdot4+16}=5\)

=>\(\left|\sqrt{2x-3}+1\right|+\left|\sqrt{2x-3}+4\right|=5\)
=>2*căn 2x-3+5=5

=>2x-3=0

=>x=3/2

a.

ĐKXĐ: \(x\ge3\)

(Tốt nhất bạn kiểm tra lại đề cái căn đầu tiên của \(\sqrt{x-3}\) là căn bậc 2 hay căn bậc 3). Vì nhìn ĐKXĐ thì thấy căn bậc 2 là không hợp lý rồi đó

Pt tương đương:

\(\sqrt{x-3}+\sqrt[3]{x^2+1}+\left(x+1\right)\left(x-2\right)=0\)

Do \(x\ge3\Rightarrow x-2>0\Rightarrow\left(x+1\right)\left(x-2\right)>0\)

\(\Rightarrow\sqrt{x-3}+\sqrt[3]{x^2+1}+\left(x+1\right)\left(x-2\right)>0\)

Pt vô nghiệm

b.

ĐKXĐ: \(x\ge-\dfrac{3}{2}\)

Pt: \(2x+3-\sqrt{2x+3}-\left(4x^2-6x+2\right)=0\)

Đặt \(\sqrt{2x+3}=t\ge0\) ta được:

\(t^2-t-\left(4x^2-6x+2\right)=0\)

\(\Delta=1+4\left(4x^2-6x+2\right)=\left(4x-3\right)^2\)

\(\Rightarrow\left[{}\begin{matrix}t_1=\dfrac{1+4x-3}{2}=2x-1\\t_2=\dfrac{1-4x+3}{2}=2-2x\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2x+3}=2x-1\left(x\ge\dfrac{1}{2}\right)\\\sqrt{2x+3}=2-2x\left(x\le1\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+3=4x^2-4x+1\left(x\ge\dfrac{1}{2}\right)\\2x+3=4x^2-8x+4\left(x\le1\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{17}}{4}\\x=\dfrac{5-\sqrt{21}}{4}\end{matrix}\right.\)

c.

ĐKXĐ: \(x\ge-1\)

\(\Leftrightarrow2\left(x^2-4x+4\right)+2\left(x+1\right)-5\left(x-2\right)\sqrt{x+1}=0\)

\(\Leftrightarrow2\left(x-2\right)^2-5\left(x-2\right)\sqrt{x+1}+2\left(x+1\right)=0\)

Đặt \(\left\{{}\begin{matrix}x-2=a\\\sqrt{x+1}=b\end{matrix}\right.\) ta được:

\(2a^2-5ab+2b^2=0\)

\(\Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=2b\\2a=b\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2\sqrt{x+1}=x-2\left(x\ge2\right)\\\sqrt{x+1}=2x-4\left(x\ge2\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}4x+4=x^2-4x+4\\x+1=4x^2-16x+16\end{matrix}\right.\) (\(x\ge2\))

\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=3\end{matrix}\right.\) (đã loại nghiệm)

a)\(\sqrt{x^2-9}+\sqrt{x^2-6x+9}=0\)

\(\Rightarrow\sqrt{\left(x-3\right)\left(x+3\right)}+\sqrt{\left(x-3\right)^2}=0\)

\(\Rightarrow\sqrt{\left(x-3\right)\left(x+3\right)}+x-3=0\)

Đặt \(x-3=t\) pt thành

\(\sqrt{t\left(t-6\right)}-t=0\)

\(\Leftrightarrow t^2-6t=t^2\)

\(\Leftrightarrow t=0\)\(\Rightarrow x-3=0\Leftrightarrow x=3\)

b)\(\sqrt{x^2-4}-x^2+4=0\)

\(\Leftrightarrow\sqrt{x^2-4}=x^2-4\)

Đặt \(\sqrt{x^2-4}=t\) pt thành

\(t=t^2\Rightarrow t\left(1-t\right)=0\)

\(\Rightarrow\left[\begin{array}{nghiempt}t=1\\t=0\end{array}\right.\).

Với \(t=0\Rightarrow\sqrt{x^2-4}=0\Rightarrow x=\pm2\) 

Với \(t=1\Rightarrow\sqrt{x^2-4}=1\)\(\Rightarrow x=\pm\sqrt{5}\)

bạn đăg từng bài thui

Đăng 1 lúc mà nhiều thế. Lần sau đăng 1 câu thôi b.

b/ \(\sqrt{x^2-4x+5}+\sqrt{x^2-4x+8}+\sqrt{x^2-4x+9}=3+\sqrt{5}\)

\(\Leftrightarrow\sqrt{\left(x-2\right)^2+1}+\sqrt{\left(x-2\right)^2+4}+\sqrt{\left(x-2\right)^2+5}=3+\sqrt{5}\)

Ta có: \(VT\ge1+2+\sqrt{5}=3+\sqrt{5}\)

Dấu = xảy ra khi \(x=2\)

c/ \(\sqrt{2-x^2+2x}+\sqrt{-x^2-6x-8}=\sqrt{3-\left(x-1\right)^2}+\sqrt{1-\left(x+3\right)^2}\)

\(\le1+\sqrt{3}\)

Dấu = không xảy ra nên pt vô nghiệm

Câu d làm tương tự

\(a,\sqrt{x^2-4}-x^2+4=0\) 

\(\Leftrightarrow\sqrt{x^2-4}=x^2-4\) 

\(\Leftrightarrow x^2-4=\left(x-4\right)^2\) 

\(\Leftrightarrow x^2-4-x^4+8x^2-16=0\)  

\(\Leftrightarrow-x^4-7x^2-20=0\) 

\(\Leftrightarrow-\left(x^4+7x^2+\frac{49}{4}\right)-\frac{31}{4}=0\) 

\(\Leftrightarrow-\left(x^2+\frac{7}{2}\right)^2=\frac{31}{4}\) 

\(\Leftrightarrow\left(x^2+\frac{7}{2}\right)=-\frac{31}{4}\) 

\(\Rightarrow\)pt vô nghiệm

a/ĐK: \(x\ge2\)

 \(PT\Leftrightarrow x^2-4=\sqrt{x^2-4}\)

Đặt \(x^2-4=t\Rightarrow x^2=t+4\)

Thay vào,phương trình đã cho tương đương với: 

\(t=\sqrt{t}\Leftrightarrow t^2=t\Rightarrow\orbr{\begin{cases}t=1\\t=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x^2-4=1\\x^2-4=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x^2=5\\x^2=4\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\sqrt{5}\\x=2\end{cases}}\)  (t/m)

a/ \(\sqrt{x^2-6x+9}=\sqrt{6-2\sqrt{5}}\)

\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=\sqrt{\left(\sqrt{5}-1\right)^2}\)

\(\Leftrightarrow|x-3|=\sqrt{5}-1\)

Làm nốt

b/ \(\sqrt{9x^2-6x+1}-3\sqrt{\frac{7-4\sqrt{3}}{9}}=0\)

\(\Leftrightarrow\sqrt{\left(3x-1\right)^2}-\sqrt{\left(2-\sqrt{3}\right)^2}\)

\(\Leftrightarrow|3x-1|=2-\sqrt{3}\)

Làm nốt

c/ \(\sqrt{2x^2-4x+2}-\sqrt{3-\sqrt{5}}=0\)

\(\Leftrightarrow\sqrt{4x^2-8x+4}-\sqrt{6-2\sqrt{5}}=0\)

\(\Leftrightarrow\sqrt{\left(2x-2\right)^2}-\sqrt{\left(\sqrt{5}-1\right)^2}=0\)

\(\Leftrightarrow|2x-2|=\sqrt{5}-1\)

Làm nốt

....

a,ĐK: x≥4

Ta có: \(2\sqrt{x-4}-\dfrac{1}{3}\sqrt{9x-36}=4-\sqrt{x-4}\)

      \(\Leftrightarrow2\sqrt{x-4}-\sqrt{x-4}=4-\sqrt{x-4}\)

      \(\Leftrightarrow2\sqrt{x-4}=4\)

      \(\Leftrightarrow\sqrt{x-4}=2\Leftrightarrow x-4=4\Leftrightarrow x=8\left(tm\right)\)

b, ĐK: x≥2

Ta có: \(3\sqrt{x-2}-\sqrt{x^2-4}=0\)

      \(\Leftrightarrow3\sqrt{x-2}-\sqrt{\left(x-2\right)\left(x+2\right)}=0\)

      \(\Leftrightarrow\sqrt{x-2}\left(3-\sqrt{x+2}\right)=0\)

      \(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-2}=0\\3-\sqrt{x+2}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2=0\\\sqrt{x+2}=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x+2=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=7\end{matrix}\right.\)