\(\text{ cos(x+\frac{\Pi}{3})+cosx=\frac{3}{2}-4sin\frac{x}{2}.sin(\frac{x}{2}+\frac{\Pi}{6})}\)

Những câu hỏi liên quan
Giải các phương trình sau:
a, sinx+cosx+1+sin2x+cos2x=0
b, sinx(1+cos2x)+sin2x=1+cos2x
c, \(\frac{1}{sinx}+\frac{1}{sin\left(x-\frac{3\pi}{2}\right)}=4sin\left(\frac{7\pi}{4}-x\right)\)
d, sin4x+cos4x=\(\frac{7}{8}cot\left(x+\frac{\pi}{3}\right)cot\left(\frac{\pi}{6}-x\right)\)
a.
\(sinx+cosx+\left(sinx+cosx\right)^2+cos^2x-sin^2x=0\)
\(\Leftrightarrow sinx+cosx+\left(sinx+cosx\right)^2+\left(cosx-sinx\right)\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1+2cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\\1+2cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=0\\cosx=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{4}+k\pi\\x=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
b.
\(sinx\left(1+2cos^2x-1\right)+2sinx.cosx=1+2cos^2x-1\)
\(\Leftrightarrow cos^2x.sinx+sinx.cosx-cos^2x=0\)
\(\Leftrightarrow cosx\left(sinx.cosx+sinx-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\Rightarrow x=\frac{\pi}{2}+k\pi\\sinx.cosx+sinx-cosx=0\left(1\right)\end{matrix}\right.\)
Xét (1), đặt \(sinx-cosx=t\Rightarrow\left[{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sinx.cosx=\frac{1-t^2}{2}\end{matrix}\right.\)
\(\Rightarrow\frac{1-t^2}{2}+t=0\)
\(\Leftrightarrow-t^2+2t+1=0\Rightarrow\left[{}\begin{matrix}t=1-\sqrt{2}\\t=1+\sqrt{2}>\sqrt{2}\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=1-\sqrt{2}\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=\frac{1-\sqrt{2}}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+arcsin\left(\frac{1-\sqrt{2}}{\sqrt{2}}\right)+k2\pi\\x=\frac{5\pi}{4}-arcsin\left(\frac{1-\sqrt{2}}{\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)
Xem thêm câu trả lời
Chứng minh đẳng thức
\(2sin\left(\frac{\pi}{2}+x\right)+sin\left(3\pi-x\right)+sin\left(\frac{3\pi}{2}+x\right)+cos\left(\frac{\pi}{2}+x\right)=cosx\)
\(2sin\left(\frac{\pi}{2}+x\right)+sin\left(3\pi-x\right)+sin\left(\frac{3\pi}{2}+x\right)+cos\left(\frac{\pi}{2}+x\right)\)
\(=2cosx+sinx-cosx-sinx\)
\(=cosx\)
Đúng 0
Bình luận (0)
\(\cos\left(x+\frac{\pi}{3}\right)+\cos x=\frac{3}{2}-4\sin\left(\frac{x}{2}\right)\cdot\sin\left(\frac{x}{2}+\frac{\pi}{6}\right)\)
\(\Leftrightarrow1-2sin^2\left(\frac{x}{2}+\frac{\pi}{6}\right)+1-2sin^2\frac{x}{2}=\frac{3}{2}-4sin\left(\frac{x}{2}\right)sin\left(\frac{x}{2}+\frac{\pi}{6}\right)\)
\(\Leftrightarrow\left[sin\left(\frac{x}{2}\right)-sin\left(\frac{x}{2}+\frac{\pi}{6}\right)\right]^2=\frac{1}{4}\)
\(\Leftrightarrow4cos^2\left(\frac{x}{2}+\frac{\pi}{12}\right).sin^2\left(\frac{\pi}{12}\right)=\frac{1}{4}\)
\(\Leftrightarrow cos^2\left(\frac{x}{2}+\frac{\pi}{12}\right)=\frac{1}{16sin^2\left(\frac{\pi}{12}\right)}=\frac{2+\sqrt{3}}{4}\)
\(\Leftrightarrow1+cos\left(x+\frac{\pi}{6}\right)=\frac{2+\sqrt{3}}{2}\)
\(\Leftrightarrow cos\left(x+\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2}\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Giải phương trình
1.\(sin^2\left(x-\frac{\pi}{6}\right)+sin^2\left(x+\frac{\pi}{6}\right)=5cosx-2\)
2.\(4sin^4x+12cos^2x=7\\\)
3.\(sin^4x+cos^{\:4}x=\frac{1}{2}\)
4.\(sin^4x+cos^4x=cos2x\)
1.
\(\Leftrightarrow\frac{1}{2}-\frac{1}{2}cos\left(2x-\frac{\pi}{3}\right)+\frac{1}{2}-\frac{1}{2}cos\left(2x+\frac{\pi}{3}\right)=5cosx-2\)
\(\Leftrightarrow-\frac{1}{2}\left[cos\left(2x-\frac{\pi}{3}\right)+cos\left(2x+\frac{\pi}{3}\right)\right]=5cosx-3\)
\(\Leftrightarrow-cos2x.cos\frac{\pi}{3}=5cosx-3\)
\(\Leftrightarrow-\frac{1}{2}cos2x=5cosx-3\)
\(\Leftrightarrow cos2x+10cosx-6=0\)
\(\Leftrightarrow2cos^2x+10cosx-7=0\)
\(\Leftrightarrow cosx=\frac{\sqrt{39}-5}{2}\)
\(\Rightarrow x=\pm arccos\left(\frac{\sqrt{39}-5}{2}\right)+k2\pi\)
Đúng 0
Bình luận (0)
2.
\(\Leftrightarrow4\left(1-cos^2x\right)^2+12cos^2x-7=0\)
\(\Leftrightarrow4cos^4x+4cos^2x-3=0\)
\(\Leftrightarrow\left(2cos^2x-1\right)\left(2cos^2x+3\right)=0\)
\(\Leftrightarrow2cos^2x-1=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\frac{\pi}{2}+k\pi\)
\(\Rightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)
Đúng 0
Bình luận (0)
3.
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x=\frac{1}{2}\)
\(\Leftrightarrow1-\frac{1}{2}\left(2sinx.cosx\right)^2=\frac{1}{2}\)
\(\Leftrightarrow1-sin^22x=0\)
\(\Leftrightarrow cos^22x=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\frac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cos2x-√3 sin2x=sin3x+1
3sin2x+4cos2x+5cos2003x=0
√3sin(x-\(\frac{\pi}{3}\))\(+sin\left(x+\frac{\pi}{6}\right)-2sin1972x=0\)
\(\sqrt{2}cos\left(\frac{x}{5}-\frac{\pi}{12}\right)-\sqrt{6}sin\left(\frac{x}{5}-\frac{\pi}{12}\right)=2sin\left(\frac{x}{5}+\frac{2\pi}{3}\right)-2sin\left(\frac{3x}{5}+\frac{\pi}{6}\right)\)
a/ Bạn coi lại đề bài, pt này có 1 nghiệm rất xấu ko giải được:
\(\Leftrightarrow1-sin^2x-2\sqrt{3}sinx.cosx=sin^3x+1\)
\(\Leftrightarrow sin^3x+sin^2x+2\sqrt{3}sinx.cosx=0\)
\(\Leftrightarrow sinx\left(sin^2x+sinx+2\sqrt{3}cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\Rightarrow x=k\pi\\sin^2x+sinx+2\sqrt{3}cosx=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow sin^2x+sinx=-2\sqrt{3}cosx\) (\(cosx\le0\))
\(\Leftrightarrow sin^2x\left(sinx+1\right)^2=12cos^2x\)
\(\Leftrightarrow sin^2x\left(sinx+1\right)^2=12\left(1-sinx\right)\left(1+sinx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}1+sinx=0\left(2\right)\\sin^2x\left(sinx+1\right)=12\left(1-sinx\right)\left(3\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow x=-\frac{\pi}{2}+k2\pi\) (thỏa mãn)
\(\left(3\right)\Leftrightarrow sin^3x+sin^2x+12sinx-12=0\)
Pt bậc 3 này có nghiệm thực thuộc \(\left(-1;1\right)\) nhưng rất xấu
Đúng 0
Bình luận (0)
b/
\(\Leftrightarrow\frac{3}{5}sin2x+\frac{4}{5}cos2x=-cos2003x\)
Đặt \(\frac{3}{5}=cosa\) với \(a\in\left(0;\pi\right)\)
\(\Rightarrow sin2x.cosa+cos2x.sina=-cos2003x\)
\(\Leftrightarrow sin\left(2x+a\right)=sin\left(2003x-\frac{\pi}{2}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2003x-\frac{\pi}{2}=2x+a+k2\pi\\2003x-\frac{\pi}{2}=\pi-2x-a+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4002}+\frac{a}{2001}+\frac{k2\pi}{2001}\\x=\frac{3\pi}{4010}-\frac{a}{2005}+\frac{k2\pi}{2005}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c/
\(\Leftrightarrow\sqrt{3}sin\left(x-\frac{\pi}{3}\right)+cos\left(\frac{\pi}{3}-x\right)=2sin1972x\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin\left(x-\frac{\pi}{3}\right)+\frac{1}{2}cos\left(x-\frac{\pi}{3}\right)=sin1972x\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{3}+\frac{\pi}{6}\right)=sin1972x\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{6}\right)=sin1972x\)
\(\Leftrightarrow\left[{}\begin{matrix}1972x=x-\frac{\pi}{6}+k2\pi\\1972x=\frac{7\pi}{6}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{11826}+\frac{k2\pi}{1971}\\x=\frac{7\pi}{11838}+\frac{k2\pi}{1973}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Phương trình : \(\sqrt{3}sinx-cosx=1\) tương đương với phương trình nào sau đây ?
A. \(sin\left(\frac{\Pi}{6}-x\right)=1\)
B. \(sin\left(\frac{\Pi}{6}-x\right)=\frac{1}{2}\)
C. \(sin\left(x-\frac{\Pi}{6}\right)=\frac{1}{2}\)
D. \(cos\left(x+\frac{\Pi}{3}\right)=\frac{1}{2}\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}sinx-\frac{1}{2}cosx=\frac{1}{2}\)
\(\Leftrightarrow sinx.cos\left(\frac{\pi}{6}\right)-cosx.sin\left(\frac{\pi}{6}\right)=\frac{1}{2}\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{6}\right)=\frac{1}{2}\)
Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:
a) \(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\)
b) \(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\)
a) Vẽ đồ thị:
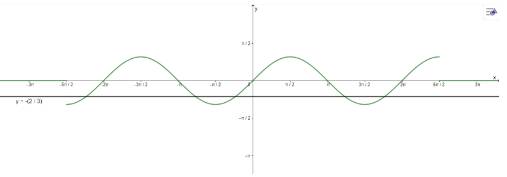
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:

\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm
Đúng 0
Bình luận (0)
Cho \(\cos 2x = \frac{1}{4}\).
Tính: \(A = \cos \left( {x + \frac{\pi }{6}} \right)\cos \left( {x - \frac{\pi }{6}} \right)\); \(B = \sin \left( {x + \frac{\pi }{3}} \right)\sin \left( {x - \frac{\pi }{3}} \right)\)
\(\begin{array}{l}A = \cos \left( {x + \frac{\pi }{6}} \right)\cos \left( {x - \frac{\pi }{6}} \right) = \frac{1}{2}\left[ {\cos \left( {x + \frac{\pi }{6} + x - \frac{\pi }{6}} \right) + \cos \left( {x + \frac{\pi }{6} - x + \frac{\pi }{6}} \right)} \right]\\A = \frac{1}{2}\left[ {\cos 2x + \cos \frac{\pi }{3}} \right] = \frac{1}{2}\left( {\frac{1}{4} + \frac{1}{2}} \right) = \frac{3}{8}\end{array}\)
\(\begin{array}{l}B = \sin \left( {x + \frac{\pi }{3}} \right)\sin \left( {x - \frac{\pi }{3}} \right) = - \frac{1}{2}\left[ {\cos \left( {x + \frac{\pi }{3} + x - \frac{\pi }{3}} \right) - \cos \left( {x + \frac{\pi }{3} - x + \frac{\pi }{3}} \right)} \right]\\B = - \frac{1}{2}\left( {\cos 2x - \cos \frac{{2\pi }}{3}} \right) = - \frac{1}{2}\left( {\frac{1}{4} + \frac{1}{2}} \right) = - \frac{3}{8}\end{array}\)
Đúng 0
Bình luận (0)
rút gọn biểu thức:
A= cosa.sin( b-c )+ cosb. sin(c-a) + cosc.sin( a-b)
B= \(sin^2x+cos\left(\frac{\pi}{3}-x\right).cos\left(\frac{\pi}{3}+x\right)\)
C=\(sin^2x+sin^2\left(\frac{2\pi}{3}+x\right)+sin^2\left(\frac{2\pi}{3}-x\right)\)
D=\(sin^2\left(\frac{\pi}{4}+x\right)-sin^2x-2sinx.sin\frac{\pi}{4}.cos\left(\frac{\pi}{4}+x\right)\)
\(A=cosa\left(sinb.cosc-cosb.sinc\right)+cosb\left(sinc.cosa-cosc.sina\right)+cosc\left(sinacosb-cosasinb\right)\)
\(A=cosasinbcosc-cosacosbsinc+cosacosbsinc-sinacosbcosc+sinacosbcosc-cosasinbcosc\)
\(A=0\)
\(B=sin^2x+\frac{1}{2}\left(cos\frac{2\pi}{3}+cos2x\right)\)
\(B=\frac{1}{2}-\frac{1}{2}cos2x-\frac{1}{4}+\frac{1}{2}cos2x\)
\(B=\frac{1}{4}\)
\(C=\frac{1}{2}-\frac{1}{2}cos2x+\frac{1}{2}-\frac{1}{2}cos\left(\frac{4\pi}{3}+2x\right)+\frac{1}{2}-\frac{1}{2}cos\left(\frac{4\pi}{3}-2x\right)\)
\(C=\frac{3}{2}-\frac{1}{2}cos2x-\frac{1}{2}\left(cos\left(\frac{4\pi}{3}+2x\right)+cos\left(\frac{4\pi}{3}-2x\right)\right)\)
\(C=\frac{3}{2}-\frac{1}{2}cos2x-cos\frac{4\pi}{3}.cos2x\)
\(C=\frac{3}{2}-\frac{1}{2}cos2x+\frac{1}{2}cos2x\)
\(C=\frac{3}{2}\)
\(D=\frac{1}{2}\left[\sqrt{2}sin\left(\frac{\pi}{4}+x\right)\right]^2-sin^2x-sinx.\sqrt{2}cos\left(\frac{\pi}{4}+x\right)\)
\(D=\frac{1}{2}\left(sinx+cosx\right)^2-sin^2x-sinx\left(sinx-cosx\right)\)
\(D=\frac{1}{2}\left(1+2sinx.cosx\right)-sin^2x-sin^2x+sinx.cosx\)
\(D=\frac{1}{2}+sinxcosx+sinxcosx=\frac{1}{2}+sin2x\)
Đúng 0
Bình luận (0)
Góc độ cao của thang dựa vào tường là 60º và chân thang cách tường 4,6 m. Chiều dài của thang là
Đúng 0
Bình luận (0)











