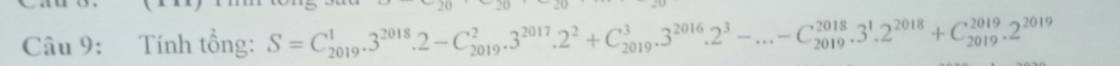gieo một con xúc xắc ba lần. xác suất để trong ba lần gieo có ít nhất 2 lần xuất hiện mặt có số chấm là chẵn Giúp em với ạ. Em đang cần gấp ạ
Ôn tập chương VI
Có thể là 2 lần chẵn 1 lần lẻ hoặc cả 3 lần đều chẵn
TH1: 2 chẵn, 1 lẻ
=>Có \(C^1_3\cdot C^1_3\cdot C^1_3=27\left(cách\right)\)
TH2: 3 lần đều chẵn
=>Có \(C^1_3\cdot C^1_3\cdot C^1_3=27\left(cách\right)\)
=>Có 27+27=54 cách
n(omega)=6*6*6=216
=>P=54/216=1/4
Đúng 0
Bình luận (0)
tìm giá trị m để bất phương trình sau có nghiệm đúng với mọi x. (m-2)x^2+2mx-2-m<0
Để phương trình có nghiệm đúng với mọi x thì
(2m)^2-4(m-2)(-m-2)<0 và m-2<0
=>4m^2+4(m^2-4)<0 và m<2
=>8m^2-16<0 và m<2
=>m^2<2
=>-căn 2<m<căn 2
Đúng 0
Bình luận (0)
Nam muốn tô màu cho một hình vuông và một hình tròn biết rằng chỉ có thể tô màu xanh màu đỏ hoặc màu vàng cho hình vuông và chỉ có thể tô màu hồng hoặc màu tím cho hình tròn quả Nam có bao nhiêu cách tô màu cho cả hai hình
Hình vuông có 3 cách tô
Hiình tròn có 2 cách tô
=> 3x2=6 cách tô
Đúng 0
Bình luận (0)
Hình vuông có 3 cách tô
Hiình tròn có 2 cách tô
=> 3x2=6 cách tô
Đúng 0
Bình luận (0)
Xét khai triển:
\(\left(-a+b\right)^{2019}=-C_{2019}^0.a^{2019}+C_{2019}^1a^{2018}.b-C_{2019}^2a^{2017}b^2+...-C_{2019}^{2018}ab^{2018}+C_{2019}^{2019}b^{2019}\)
Thay \(a=2;b=3\)
\(\Rightarrow1=-2^{2019}+C_{2019}^1.3^{2018}.2-C_{2019}^2.3^{2017}.b^2+...-C_{2019}^{2018}32^{2018}+C_{2019}^{2019}.2^{2019}\)
\(\Rightarrow S=2^{2019}+1\)
Đúng 1
Bình luận (2)
Cho Tam giác ABC có M trung điểm BC biểu diễn đồ thị CM và AB và AC véctơ
vecto CM=1/2*vecto CB
=1/2(vecto CA+veco AB)
=-1/2*vecto AC+1/2*vecto AB
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB=12 , BC= 15,AC = 13 a) tính số đo các góc của tam giác ABC b) tính diện tích tam giác ABC , bán kính đường tròn ngoại tiếp , bán kính đường tròn nội tiếp tam giác ABC
a: \(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{11}{39}\)
=>góc A=74 độ
\(cosB=\dfrac{12^2+15^2-13^2}{2\cdot12\cdot15}=\dfrac{5}{9}\)
=>góc B=56 độ
=>góc C=50 độ
b: \(S_{ABC}=\dfrac{1}{2}\cdot15\cdot13\cdot sin50\simeq74,69\left(cm^2\right)\)
AB/sinC=2R
=>2R=12/sin50
=>R=7,83(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn đường kính BC , BC = 2a . Tìm giá trị lớn nhất của diện tích tam giác ABC theo a
Giúp tớ với
Do tam giác ABC nội tiếp đường tròn đường kính BC \(\Rightarrow\Delta ABC\) vuông tại A
Đặt \(AB=x\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{4a^2-x^2}\)
\(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}x\sqrt{4a^2-x^2}\le\dfrac{1}{4}\left(x^2+4a^2-x^2\right)=a^2\)
\(S_{max}=a^2\) khi \(x=\sqrt{4a^2-x^2}\Rightarrow x=a\sqrt{2}\) hay tam giác vuông cân tại A
Đúng 1
Bình luận (0)
Chứng minh rằng : 4(\(\sin\)6α+\(\cos\)6α)-2(\(\sin\)4α+\(\cos\)4α)=1+\(\cos\)4α
VT=4[(sin^2a+cos^2a)^3-3sin^2a*cos^2a]-2[1-2*sin^2cos^2a]
=4-12sin^2a*cos^2a-2+4sin^2a*cos^2a
=2-8*sin^2acos^2a
=1+cos4a=VP
Đúng 0
Bình luận (0)
Giúp em vs ạ
\(\dfrac{1}{sin^4\left(x+\dfrac{\pi}{2}\right)\left[tan^2x+tan^2\left(\dfrac{\pi}{2}-x\right)+2\right]}=\dfrac{1}{cos^4x\left(tan^2x+cot^2x+2\right)}\)
\(=\dfrac{1}{cos^4x\left(tanx+cotx\right)^2}=\dfrac{1}{cos^4x\left(\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}\right)^2}\)
\(=\dfrac{1}{cos^4x\left(\dfrac{sin^2x+cos^2x}{sinx.cosx}\right)^2}=\dfrac{1}{cos^4x.\dfrac{1}{sin^2x.cos^2x}}\)
\(=\dfrac{sin^2x}{cos^2x}=tan^2x\)
Đúng 2
Bình luận (0)
Chu vi đường tròn: \(2\pi R=80\pi\left(cm\right)\)
\(\Rightarrow\) Độ dài cung tròn:
\(80\pi.\dfrac{\dfrac{\pi}{17}}{2\pi}=\dfrac{40\pi}{17}\left(cm\right)\)
Đúng 0
Bình luận (0)